逻辑回归模型可以看作是 “只有一个神经元” 的分类器,它包含“一个做线性运算的地方,还有一个激活函数”。
本节课核心内容是 “反向传播算法的详细推导过程”
首先看下图,我们能看到一个神经网络模型,这个模型是用来做图像识别,识别一张图片里是否有猫 (二元分类模型)
下图可以看见模型的成本函数 cost function,它是损失函数 loss function 平均值
损失函数 loss function 则是交叉熵函数
每一次梯度下降法迭代,都会对参数矩阵做一次修改:W[p] = W[p] - alpha x (成本函数对 W[p] 的导数)
在下图中,可以看到相关的参数矩阵分别是 w[1], b[1], w[2], b[2], w[3], b[3]

让我们回忆一下上节课“前向传播”的内容,如下图
前向传播 (由输入 X 计算最终的 a[3],或者说 yhat 的过程公式如下)
z[1] = w[1] X + b[1]
a[1] = sigmoid (z[1])
z[2] = w[2] a[1] + b[2]
a[2] = sigmoid (z[2])
z[3] = w[3] a[2] + b[3]
a[3] = sigmoid (z[3])

经过一次前向传播后,我们已经计算出了当前的 w[1], b[1], w[2], b[2], w[3], b[3],以及 z[1], a[1], z[2], a[2], z[3], a[3]
那么,在应用梯度下降法,需要求导时,也可以利用这些已经计算出来的数值矩阵
从后向前求导,第一步是求 成本函数 cost function 相对 w[3] 的导数,求导过程如下
首先是煤老板的计算过程

然后是我自己的求导过程

第二步是求 “成本函数对 W[2] 的导数”
如下图,是煤老板对 “损失函数对 W[2] 求导” 的推导过程
他首先写出导数的 chain rule 形式,随后针对每一项 (或几项) 写出式子
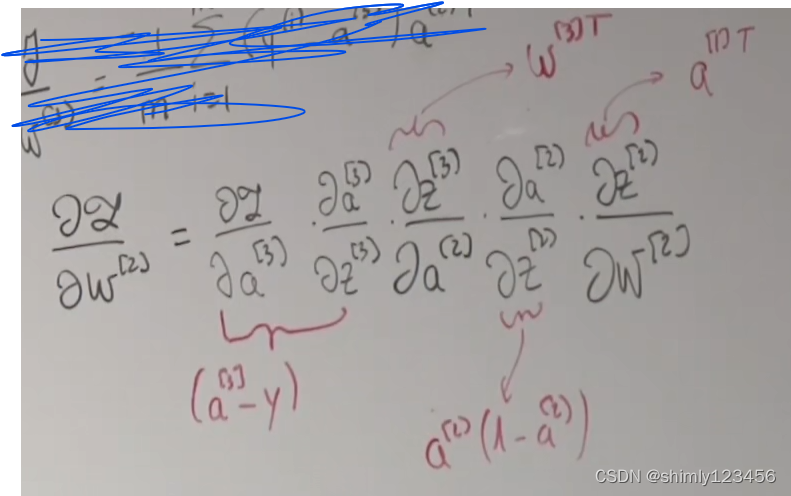
然后再用形状分析法,把它们整理好顺序,并组合在一起形成完整的式子,如下图
(煤老板在这里提到,在对矩阵乘法时,有些项的顺序需要变换,但由于课时有限无法进入那些细节,某个 lecture notes 上有更加严格的方法,在这里我们可以使用 chain_rule + shape_analysis 快速调整顺序,得到正确的公式)
需要注意的是,每一次对 sigmoid (听煤老板的意思,还包括所有任意 activation 激活函数) 求导时,都会出现一个 element-wise product。整理后,最后的公式如下图所示。

接下来是我自己手算的版本


接下来开始这堂课的下一个部分:如何提高神经网络的性能?
通常使用简单的神经网络并不会得到好结果,我们需要使用一些技术去提高模型性能
技巧1. 选用合适的激活函数(尝试不同的激活函数)
如下图,是 sigmoid 和 ReLU 激活函数

下图是 tanh 函数和它的导数
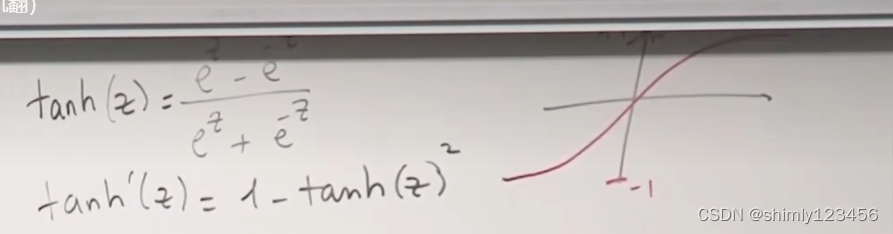
那么这三个激活函数分别有什么优劣呢?
sigmoid 优点:用在分类任务上很方便 (值域在(0, 1)) 缺点:位于高激活和低激活状态时(z很大或者很小),斜率非常接近0,训练速度慢 (这也叫梯度消亡现象 gradient vanishing)
tanh 优缺点和 sigmoid 非常相似
ReLU 可以保证较快的训练速度
ReLU 的导数可以用如下图的示性函数 indicator 来表示(当 z > 0 时,函数值为1,否则为 0)
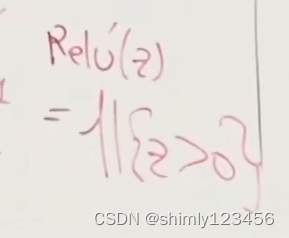
为什么我们需要激活函数?
(因为,如果没有激活函数,无论神经网络多深,都会退化成普通的线性方程 ----- 即,线性回归)如下两图
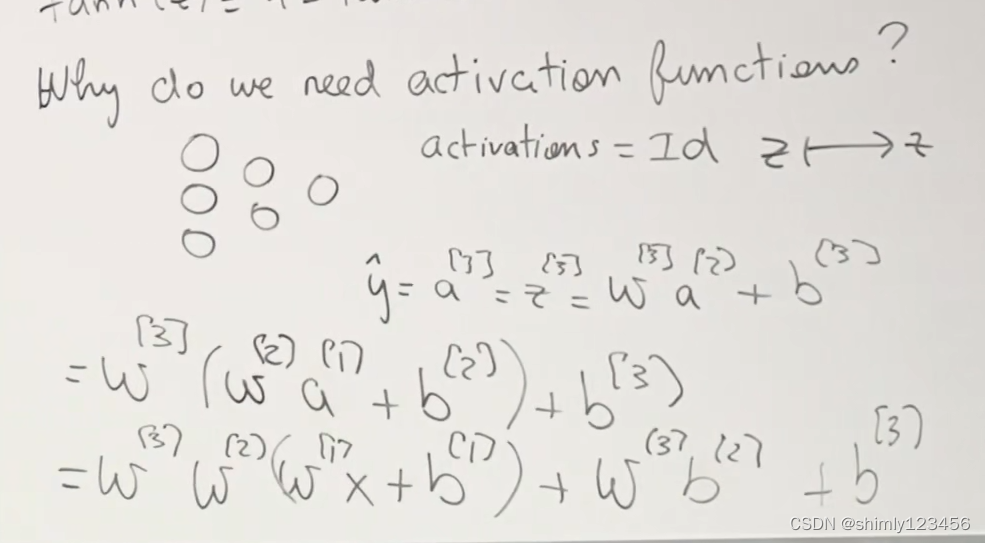
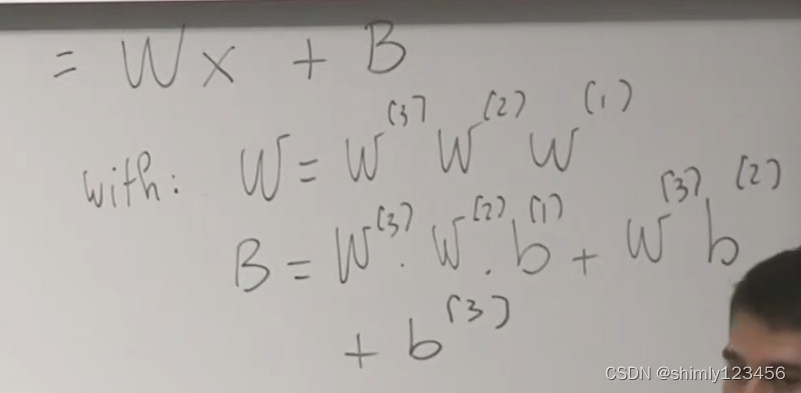
因此,这就是神经网络中必须有激活函数的原因
每一层、每一个神经元对于激活函数的选择实际上算是 Hyper-parameters
在实践中,我们不会随机选择激活函数/hyperparameters,而是尝试一些,然后选择一个看起来对训练模型有效的
在深度学习中,有许多实验结果,而我们通常并不能真正理解为什么某些激活函数比其它激活函数更有效
技巧2. 选择合适的初始化方法
1.最好对输入样本进行正则化
原因:假设 X = (x1, x2) ,即输入样本有两个维度,而 x1 维度的绝对值通常位于 10000以上,x2 维度绝对值通常位于 1以内
那么 x2 维度将完全被 x1 维度淹没。同时,也会得到一个很大的 z 值,使得我们在做梯度下降法的时候非常慢
对输入样本进行正则化的步骤如下面两图:
(1) 首先先计算 x1 和 x2 两个维度的均值,然后用样本减去均值,就会有如下图1的偏移

(2) 随后计算 x1 和 x2 的方差,让样本除以标准差,就会得到如下图所示的圆

此时,避免了 x2 属性被淹没的问题,也使得激活函数获得的输入更小,做梯度下降法更快
还有一个好处,那就是在对输入进行正则化后,损失函数 loss function 的形状会发生变化,如下图

这样一来在使用梯度下降法的时候,会更快且更有效(因为做梯度下降法时,脚步会沿和切线垂直的方向运动)
需要注意的是:正则化中计算出的 “均值” 和 “标准差” 是使用训练集的样本计算出来的,随后在评估过程中,我们不会去计算 测试集 的“均值” 和 “标准差”,而是直接使用训练集计算出的 “均值”、“标准差” 去正则化测试集的输入
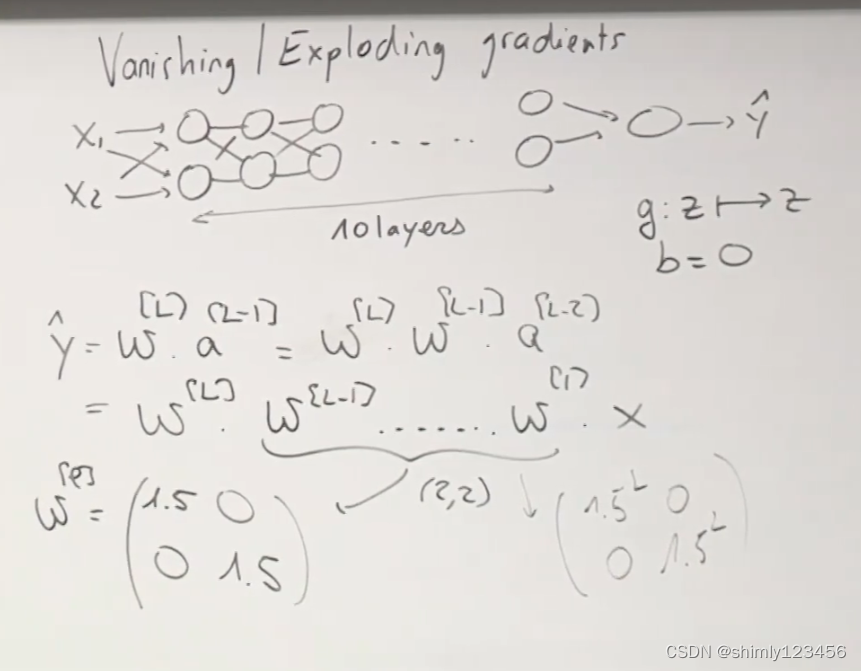
技巧3. 还有一个问题需要解决:Vanishing / Exploding gradients
设想激活函数是 f(x) = x,偏置矩阵为 b = 0
那么如下图所示,整个神经网络会退化成一个线性回归
在神经网络很深的情况下
如果所有的权重矩阵稍大于 1,或者稍小于1,这些偏差经过指数级的累积,最后就会发生指数爆炸,或者非常接近于 0
于是我们最终得到的 yhat 也会非常大,或者非常小
在进行反向传播的时候,如果求得的导数是稍微大于1,或者稍微小于1,在进行参数矩阵优化的时候,也可能使得梯度过大、或者过小
这个现象也叫做 Vanishing / Exploding gradients
那么,如何解决 Vanishing / Exploding gradients 这个现象呢?
一种不太完美的方式,就是尝试去 “正确地” 初始化权重矩阵
看看下面这张图,这里有一个神经元,它接受 “n维输入”,然后输出一个 activation output
此时的线性计算结果是 Z = w1x1 + w2x2 + … + wnxn
根据之前的描述,n维输入 X 已经被正则化到 (-1, 1) 这个区间,此时,w1, w2, …, wn 必须要足够小,才能防止梯度爆炸问题。
但也不能太小,否则就会出现 Z = 0
一个比较直觉的想法是:尽可能让权重矩阵的 W 的每一个元素接近 (1/n)

有一些在实践中,经过实验,公认比较有效的初始化矩阵的方法
对于 sigmoid 激活函数,我们可以像下面这样写参数矩阵的初始化代码:
W[p] = np.random.randn(shape) "element-wise product" np.sqrt(1/n[p-1])
# 对于第 p 层参数矩阵的初始化方法:我们认为权重矩阵的初始值应该和 这一层的输入个数 成一个比例
如果使用 ReLU 激活函数,我们可以像下面这样写参数矩阵的初始化代码:
W[p] = np.random.randn(shape) "element-wise product" np.sqrt(2/n[p-1])
# 其实就是把 1 改成了 2

如下图,适用于 tanh 激活函数的初始化方法是 Xavien Initialization
另外一种初始化方法是更下面的那行公式,它同时考虑 n[p] 和 n[p-1]。
这里的直觉是:前向传播时,我们要考虑 n[p-1] (即,这一层神经元的输入数量);在反向传播时,我们要考虑 n[p] (即,这一层神经元的输出数量),于是我们这里求了一个几何平均,如下图更下面的那行公式

需要注意的一点是:从上面的内容来看,我们在初始化权重矩阵的时候会引入随机性 (np.random)。如果不这么做,那么所有的神经元会趋向于学习相同的东西
接下来我们来讨论一下神经网络的优化:
首先先来比较普通梯度下降法和随机梯度下降法
普通梯度下降法:使用所有的样本来求梯度,在对 loss function 进行 minimization 时,会沿着和切线垂直的方向前进。很慢,每优化一步都代价巨大。
随机梯度下降法:一次使用一个样本来求梯度,你会发现它走的方向更随机,是一种振荡式的前进。很快,每一步的优化效果比较差。
小批次梯度下降法:直觉是,我们使用一个小批次(比如100个样本)对 loss function 求导,这100个样本已经足够我们在做优化的时候找到一个正确的方向。这种方法同时保证了速度以及每一步的优化质量
如下图的 Algo 算法伪代码,就是一种小批次梯度下降法,一次使用 1000 个样本做训练。

如下图,批次梯度下降法学习曲线更平滑,而小批次梯度下降法会更震荡

如下图是 loss function 绘制出来像个椭圆的情况
正常的梯度下降法,尤其是 SGD 随机梯度下降法,很容易出现像红线一样反复震荡的情况
而如果加上动量算法,就会出现绿线的情况,步子慢慢笔直朝中心走去
动量算法:在做优化过程中,对以前求得的梯度求平均。
于是,在 y 轴上反复震荡的情况,经过求平均,会逐渐趋近于0
而在 x 轴上没有反复震荡,所以这部分的速度和步长不会改变
于是就出现向绿线一样,优化的步子慢慢笔直朝中心走去

如下图是动量算法的公式,我们并不会对过去的 梯度 做严格平均,而是使用 “灰度”
这种做法的好处是:1. 节省性能 2. 节省空间 3. 记录 velocity 的变量跟当前的梯度关联更大,而和久远之前的 梯度 关联更小 (这更加符合直觉)























 2626
2626











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








