1. RNN

h t = σ ( W ( h h ) h t − 1 + W ( h x ) x [ t ] ) (5) h_t=\sigma(W^{(hh)}h_{t-1}+W^{(hx)}x_{[t]}) \tag{5} ht=σ(W(hh)ht−1+W(hx)x[t])(5)
y ^ t = s o f t m a x ( W ( S ) h t ) (6) \hat{y}_t=softmax(W^{(S)}h_t) \tag{6} y^t=softmax(W(S)ht)(6)
其中:
x 1 , . . x T x_1,..x_T x1,..xT: 表示总共T个词汇的预料中各个词语的词向量。
h t h_t ht是每次迭代的隐层输出。
x t ∈ R d x_t \in R^d xt∈Rd: 第t步的输入,词向量维度d。
$W^{hx} \in R^{D_h \times d } $: 输入x的权重矩阵。
W h h ∈ R D h × D h W^{hh} \in R^{D_h \times D_h} Whh∈RDh×Dh: 前一轮 h t − 1 h_{t-1} ht−1的权重矩阵。
h t − 1 ∈ R D h h_{t-1} \in R^{D_h} ht−1∈RDh: 前一轮迭代的非线性函数输出。
σ ( ) \sigma() σ(): 非线性激活函数,例如sigmoid。
y ^ t ∈ R ∣ V ∣ \hat{y}_t \in R^{|V|} y^t∈R∣V∣: 每一轮迭代t针对全部词汇的输出概率分布。|V|是其label的维度,如果是分类就是类的个数。W s ∈ R ∣ V ∣ × D h W^{s} \in R^{|V| \times D_h} Ws∈R∣V∣×Dh
损失函数
通常是交叉熵,迭代t中,交叉熵如下(其中
y
t
,
j
y_{t,j}
yt,j是真实标签):
J
(
t
)
(
θ
)
=
−
∑
j
=
1
∣
V
∣
y
t
,
j
×
log
(
y
^
t
,
j
)
(7)
J^{(t)}(\theta)=-\sum_{j=1}^{|V|}y_{t,j}\times \log(\hat{y}_{t,j}) \tag{7}
J(t)(θ)=−j=1∑∣V∣yt,j×log(y^t,j)(7)
在规模为T的语料(相当于样本个数)上,交叉熵错误的计算:
J
=
−
1
T
∑
t
=
1
T
J
(
t
)
(
θ
)
=
−
1
T
∑
t
=
1
T
∑
j
=
1
∣
V
∣
y
t
,
j
×
log
(
y
^
t
,
j
)
(8)
J=-\frac{1}{T}\sum_{t=1}^{T}J^{(t)}(\theta)=-\frac{1}{T}\sum_{t=1}^{T}\sum_{j=1}^{|V|}y_{t,j}\times \log{(\hat{y}_{t,j})} \tag{8}
J=−T1t=1∑TJ(t)(θ)=−T1t=1∑Tj=1∑∣V∣yt,j×log(y^t,j)(8)
梯度和长期依赖(Long-Term Dependencies)问题
梯度计算
在某轮迭代tt中考虑公式5、6,用于计算RNN错误
d
E
/
d
W
dE/dW
dE/dW,我们对每一步迭代计算错误率总和。那么每一步tt的错误率
d
E
t
/
d
W
dE_t/dW
dEt/dW均可通过前面所列的计算出来。
∂
E
∂
W
=
∑
t
=
1
T
∂
E
t
∂
W
(10)
\frac{\partial{E}}{\partial{W}}=\sum_{t=1}^T\frac{\partial E_{t}}{\partial{W}}\tag{10}
∂W∂E=t=1∑T∂W∂Et(10)
链式法则求导得到每一个迭代步长错误率,
d
h
t
/
d
h
k
dh_t/dh_k
dht/dhk为对之前kk次迭代的偏导数。
∂
E
t
∂
W
=
∑
k
=
1
t
∂
E
t
∂
y
t
∂
y
t
∂
h
t
∂
h
t
∂
h
k
∂
h
k
∂
W
(11)
\frac{\partial E_{t}}{\partial W}=\sum_{k=1}^t \frac{\partial E_{t}}{\partial y_{t}} \frac{\partial y_{t}}{\partial h_{t}}\frac{\partial h_{t}}{\partial h_{k}} \frac{\partial h_{k}}{\partial W} \tag{11}
∂W∂Et=k=1∑t∂yt∂Et∂ht∂yt∂hk∂ht∂W∂hk(11)
问题在于
∂
h
t
∂
h
k
\frac{ \partial h_{t} }{ \partial h_{k}}
∂hk∂ht。
∂
h
t
∂
h
k
=
∏
j
=
k
+
1
t
∂
h
j
∂
h
j
−
1
=
∏
j
=
k
+
1
t
W
h
h
T
×
σ
′
(12)
\frac{\partial h_{t}}{\partial h_{k}}=\prod_{j=k+1}^t \frac{\partial h_{j}}{\partial h_{j-1}}=\prod_{j=k+1}^t W_{hh}^T \times \sigma' \tag{12}
∂hk∂ht=j=k+1∏t∂hj−1∂hj=j=k+1∏tWhhT×σ′(12)

对于每个元素求导
W
D
n
×
D
n
W^{D_n \times D_n}
WDn×Dn,其Jacobian矩阵:
∂
h
j
∂
h
j
−
1
=
[
∂
h
j
∂
h
j
−
1
,
1
…
∂
h
j
∂
h
j
−
1
,
D
n
]
=
[
∂
h
j
,
1
∂
h
j
−
1
,
1
…
∂
h
j
,
1
∂
h
j
−
1
,
D
n
⋮
⋱
⋮
∂
h
j
,
D
n
∂
h
j
−
1
,
1
…
∂
h
j
,
D
n
∂
h
j
−
1
,
D
n
]
(13)
\frac{\partial h_{j}}{\partial h_{j-1}}=[\frac{\partial h_{j}}{\partial h_{j-1,1}} \dots \frac{\partial h_{j}}{\partial h_{j-1,D_n}}]=\begin{bmatrix}\frac{\partial h_{j,1}}{\partial h_{j-1,1}} & \dots & \frac{\partial h_{j,1}}{\partial h_{j-1,D_n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial h_{j,D_n}}{\partial h_{j-1,1}} & \dots & \frac{\partial h_{j,D_n}}{\partial h_{j-1,D_n}} \end{bmatrix} \tag{13}
∂hj−1∂hj=[∂hj−1,1∂hj…∂hj−1,Dn∂hj]=⎣⎢⎢⎡∂hj−1,1∂hj,1⋮∂hj−1,1∂hj,Dn…⋱…∂hj−1,Dn∂hj,1⋮∂hj−1,Dn∂hj,Dn⎦⎥⎥⎤(13)
结合10,11,12,得到:
∂
E
∂
W
=
∑
t
=
1
T
∑
k
=
1
t
∂
E
t
∂
y
t
∂
y
t
∂
h
t
(
∏
j
=
k
+
1
t
∂
h
j
∂
h
j
−
1
)
∂
h
k
∂
W
(14)
\frac{\partial E}{\partial W}=\sum_{t=1}^T\sum_{k=1}^t \frac{\partial E_{t}}{\partial y_{t}} \frac{\partial y_{t}}{\partial h_{t}}(\prod_{j=k+1}^t \frac{\partial h_{j}}{\partial h_{j-1}}) \frac{\partial h_{k}}{\partial W} \tag{14}
∂W∂E=t=1∑Tk=1∑t∂yt∂Et∂ht∂yt(j=k+1∏t∂hj−1∂hj)∂W∂hk(14)
梯度爆炸:如果Jacobian矩阵的值非常大,参照激活函数及网络参数可能会出现梯度爆炸,即所谓的梯度爆炸问题。
https://zhuanlan.zhihu.com/p/28687529
sigmoid:
f
(
z
)
=
1
/
(
1
+
e
x
p
(
−
z
)
)
f
(
z
)
′
=
f
(
z
)
(
1
−
f
(
z
)
)
f(z) = 1 / (1 + exp( − z)) \\ f(z)' = f(z)(1 − f(z))
f(z)=1/(1+exp(−z))f(z)′=f(z)(1−f(z))

sigmoid函数在两端的导数均为0,近乎呈直线状(导数为0,函数图像为直线),此种情况下可称相应的神经元已经饱和。两函数的梯度为0,使前层的其它梯度也趋近于0。由于矩阵元素数值较小,且矩阵相乘数次(t - k次)后,梯度值迅速以指数形式收缩(意思相近于,小数相乘,数值收缩,越来越小),最终在几个时间步长后完全消失。“较远”的时间步长贡献的梯度变为0,这些时间段的状态不会对你的学习有所贡献:你最终还是无法学习长期依赖。梯度消失不仅存在于循环神经网络,也出现在深度前馈神经网络中。区别在于,循环神经网络非常深(本例中,深度与句长相同),因此梯度消失问题更为常见。
解决:
解决梯度爆炸问题,Thomas Mikolov首先提出了一个简单的启发性的解决方案,就是当梯度大于一定阈值的的时候,将它截断为一个较小的数。
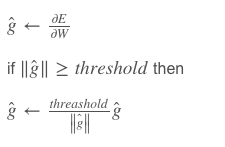
解决梯度弥散的问题,两种方法。第一种方法是将随机初始化 W ( h h ) W^{(hh)} W(hh)改为一个有关联的矩阵初始化。第二种方法是使用ReLU(Rectified Linear Units)代替sigmoid函数。ReLU的导数不是0就是1.因此不太可能会出现梯度消失的情况。
当间隔不断增大时,RNN 会丧失学习到连接如此远的信息的能力。Bengio, et al. (1994)
借助LSTM架构。LSTM只有状态 C t C_t Ct传递。

展开为:
C
t
=
f
t
C
t
−
1
+
i
t
x
t
=
σ
(
W
f
X
t
+
b
f
)
C
t
−
1
+
σ
(
W
i
X
t
+
b
i
)
X
t
h
t
=
t
a
n
h
(
C
t
)
∗
o
i
C_t = f_t C_{t-1}+i_tx_t =\sigma(W_f X_t+b_f)C_{t-1} + \sigma(W_iX_t+b_i)X_t \\ h_t = tanh(C_t)*o_i
Ct=ftCt−1+itxt=σ(WfXt+bf)Ct−1+σ(WiXt+bi)Xtht=tanh(Ct)∗oi
求导:
∏
j
=
k
+
1
t
∂
h
j
∂
C
j
−
1
=
∏
j
=
k
+
1
t
t
a
n
h
′
σ
(
W
f
X
t
+
b
f
)
\prod_{j=k+1}^t \frac{\partial h_{j}}{\partial C_{j-1}} = \prod_{j=k+1}^t tanh' \sigma(W_f X_t+b_f)
j=k+1∏t∂Cj−1∂hj=j=k+1∏ttanh′σ(WfXt+bf)
其函数图像为:基本不是0就是1。

现代的LSTM使用的是累加的形式计算状态。这种形式导致导数也是累加形式,因此避免了梯度消失。
细胞状态在整个链上运行,只有一些少量的线性交互。信息在上面流传保持不变会很容易。
双向RNN
如何利用上下文信息做预测。
Irsoy等人设计了一个双向深度神经网络,在每一个时间节点t,这个网络有两层神经元,一层从左向右传播,另一层从右向左传播。为了保证任何时刻t都有两层隐层,这个网络需要消耗两倍的存储量来存储权重和偏置等参数。最终的分类结果是由两层RNN隐层组合来产生最终的结果。

h
→
t
=
f
(
W
→
x
t
+
V
→
h
→
t
−
1
+
b
→
)
h
←
t
=
f
(
W
←
x
t
+
V
←
h
←
t
+
1
+
b
←
)
y
^
t
=
g
(
U
h
t
+
c
)
=
g
(
U
[
h
→
t
;
h
←
t
]
+
c
)
\overset{\rightarrow }{h}_t = f \left ( \overset{\rightarrow }{W}x_t + \overset{\rightarrow }{V}\overset{\rightarrow }{h}_{t-1}+\overset{\rightarrow }{b} \right ) \\ \overset{\leftarrow }{h}_t = f \left ( \overset{\leftarrow }{W}x_t + \overset{\leftarrow }{V}\overset{\leftarrow }{h}_{t+1}+\overset{\leftarrow }{b} \right ) \\ \hat{y}_t=g\left ( Uh_t+c \right )=g\left ( U\left[\overset{\rightarrow }{h}_t;\overset{\leftarrow }{h}_t\right] +c\right )
h→t=f(W→xt+V→h→t−1+b→)h←t=f(W←xt+V←h←t+1+b←)y^t=g(Uht+c)=g(U[h→t;h←t]+c)
2. LSTM
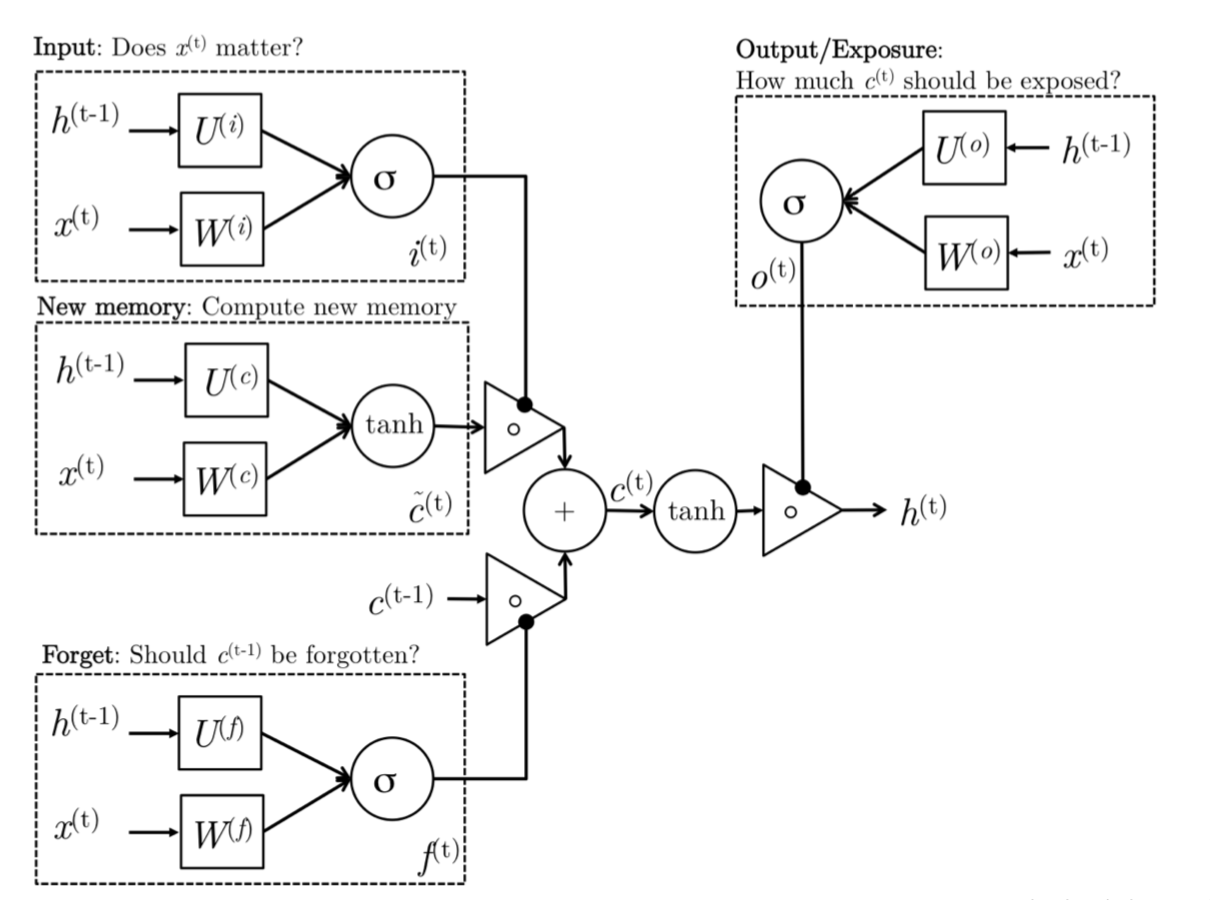
2.1 遗忘门:
对过去记忆单元是否对当前记忆单元的计算有用做出评估。例如出现了新的主语,希望忘记旧的主语。

f t = σ ( W ( f ) x t + U ( f ) h t − 1 ) (Forget gate) f_t = \sigma \left( W^{\left( f\right)}x_t+U^{\left(f \right)}h_{t-1}\right) \tag{Forget gate} ft=σ(W(f)xt+U(f)ht−1)(Forget gate)
2.2 输入门
在产生新记忆之前,我们需要判定一下我们当前看到的新词到底重不重要,这就是输入门的作用。
输入门根据输入词和过去隐层状态共同判定输入值是否值得保留,从而判定它以何种程度参与生成新的记忆(或者说对新的记忆做一个约束)。因此,它可以作为输入信息更新的一个指标。
sigmoid层称 “输入门层” 决定什么值我们将要更新。然后,一个 tanh 层创建一个新的候选值向量,[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-M3mitoKF-1602239926120)(https://math.jianshu.com/math?formula=%5Ctilde%7BC%7D_t)],会被加入到状态中。下一步,我们会讲这两个信息来产生对状态的更新。
在我们语言模型的例子中,我们希望增加新的主语的性别到细胞状态中,来替代旧的需要忘记的主语,使用输入词 x t x_t xt和过去隐层状态 h t − 1 ht−1 ht−1来产生新的记忆 c ~ t \tilde{c}_t c~t.

产生新的记忆之后,就涉及更新细胞状态C。
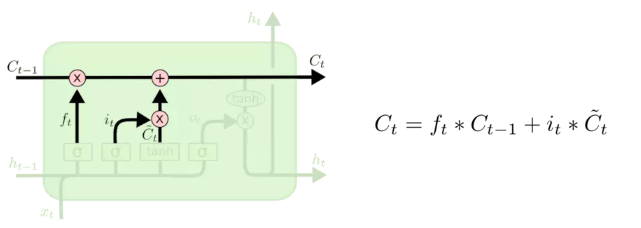
2.3 输出门
决定输出什么值,输出主要是依赖于 cell 的状态 C t C_t Ct,但是又不仅仅依赖于 C t C_t Ct。

- 使用一个sigmoid层来(计算出)决定 C t C_t Ct权重,决定哪些信息会被输出;
- 把 C t C_t Ct通过一个 tanh 层([-1, 1]),然后把 tanh 层的输出和 sigmoid 层计算出来的权重相乘,这样就得到了最后输出的结果。
参数量: W i , U i , W f , U f , W o , U o , W c , U c W_i, U_i, W_f, U_f, W_o, U_o, W_c, U_c Wi,Ui,Wf,Uf,Wo,Uo,Wc,Uc
3. GRU
使用门限激活函数改进RNN的一种方法。

GRU有两种门:
z
t
=
σ
(
W
(
z
)
x
t
+
U
(
z
)
h
t
−
1
)
(Update gate)
z_t = \sigma \left( W^{\left(z \right)}x_t + U^{\left ( z \right )}h_{t-1}\right) \tag{Update gate}
zt=σ(W(z)xt+U(z)ht−1)(Update gate)
r t = σ ( W ( r ) x t + U ( r ) h t − 1 ) (Reset gate) r_t = \sigma \left ( W^{\left ( r \right )}x_t + U^{\left ( r \right )}h_{t-1} \tag{Reset gate}\right ) rt=σ(W(r)xt+U(r)ht−1)(Reset gate)
h ~ t = tanh ( r t ∘ U h t − 1 + W x t ) (New memory) \tilde{h}_t = \tanh \left ( r_t \circ Uh_{t-1}+Wx_t \right ) \tag{New memory} h~t=tanh(rt∘Uht−1+Wxt)(New memory)
h t = ( 1 − z t ) ∘ h ~ t + z t ∘ h t − 1 (Hidden state) h_t = \left ( 1-z_t \right )\circ \tilde{h}_t +z_t \circ h_{t-1} \tag{Hidden state} ht=(1−zt)∘h~t+zt∘ht−1(Hidden state)
x t ∈ R d x_t \in R^d xt∈Rd: 第t步的输入,词向量维度d。
$W, W^{z}, W^{r} \in R^{D_h \times d } $: 输入x的权重矩阵。
U , U r , U z ∈ R D h × D h U, U^{r}, U^{z} \in R^{D_h \times D_h} U,Ur,Uz∈RDh×Dh: 前一轮 h t − 1 h_{t-1} ht−1的权重矩阵。
h t − 1 ∈ R D h h_{t-1} \in R^{D_h} ht−1∈RDh: 前一轮迭代的非线性函数输出。
σ ( ) \sigma() σ(): 非线性激活函数,例如sigmoid。
y ^ t ∈ R ∣ V ∣ \hat{y}_t \in R^{|V|} y^t∈R∣V∣: 每一轮迭代t针对全部词汇的输出概率分布。|V|是其label的维度,如果是分类就是类的个数。
W s ∈ R ∣ V ∣ × D h W^{s} \in R^{|V| \times D_h} Ws∈R∣V∣×Dh
- 新记忆产生:一个新的记忆 h ~ \tilde{h} h~ 是由过去的隐含状态 h t − 1 h_{t-1} ht−1和新的输入 x t x_t xt共同得到的。也就是说,这个阶段能够对新观察到的信息(词)和历史的隐层状态 h t − 1 h_{t-1} ht−1进行合理合并,根据语境向量 h ~ t \tilde{h}_t h~t总结这个新词以何种状态融合。
- 重置门:重置信号 r t r_t rt会判定 h t − 1 h_{t-1} ht−1对结果 h ~ \tilde{h} h~的重要程度。如果 h t − 1 h_{t-1} ht−1和新的记忆的计算不相关,那么重置门能够完全消除过去的隐层信息(状态)。
- 更新门:更新信号$z_t 会 决 定 以 多 大 程 度 将 会决定以多大程度将 会决定以多大程度将h_{t-1} 向 下 一 个 状 态 传 递 。 比 如 , 如 果 向下一个状态传递。比如,如果 向下一个状态传递。比如,如果z_t \approx 1 , 则 ,则 ,则h_{t-1} 几 乎 完 全 传 递 给 几乎完全传递给 几乎完全传递给h_t 。 相 反 的 , 如 果 。相反的,如果 。相反的,如果z_t \approx 0 , 新 的 ,新的 ,新的\tilde{h}$前向传递给下一层隐层。
- 隐层状态:使用过去隐层输入 h t − 1 h_{t-1} ht−1和 x t x_t xt最终产生了隐层状态 h t h_t ht。
参数有 W , W r , W z , U , U r , U z W, W^r,W^z,U, U^r, U^z W,Wr,Wz,U,Ur,Uz

SRU

应用
RNN核心在于对向量的序列进行操作:输入可以是序列,输出也可以是序列,在最一般化的情况下输入输出都可以是序列。

每个正方形代表一个向量,箭头代表函数(比如矩阵乘法)。输入向量是红色,输出向量是蓝色,绿色向量装的是RNN的状态(马上具体介绍)。从左至右为:
- 非RNN的普通过程,从固定尺寸的输入到固定尺寸的输出(比如图像分类)。
- 输出是序列(例如图像标注:输入是一张图像,输出是单词的序列)。
- 输入是序列(例如情绪分析:输入是一个句子,输出是对句子属于正面还是负面情绪的分类)。
- 输入输出都是序列(比如机器翻译:RNN输入一个英文句子输出一个法文句子)。
- 同步的输入输出序列(比如视频分类中,我们将对视频的每一帧都打标签)。





























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










