算法笔记——素数筛

算法笔记——素数筛

求素数是我们经常会遇到的问题，如何能提高求解素数的效率对我们解决问题至关重要，本文会记录四种求素数的方法，分别是直观算法、朴素算法，埃氏筛法和欧拉筛法

素数的定义

素数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。（百度百科）
这里需要注意素数的范围是大于1的自然数，即0和1都不是素数

直观算法

直观算法是通过素数的定义来实现的，即除了1和它本身外不再有其他因素，那么我们要判断n是不是素数，只需要遍历看n是否能被2到n-1中的某个数整除即可

注：这种算法在实际判断中不会用到，这里只是为了解释素数的判断原理，实际判断某个数是否为素数推荐用下面的朴素算法

时间复杂度：O(n²)

代码实现

//从2到x-1遍历 
bool isPrime(int x)
{
	//0和1特判 
	if(x==0||x==1)
		return false;
	for(int i=2;i<x;i++)
	{
		if(x%i==0)
			return false;
	}
	return true;
}

朴素算法

朴素算法对于上面直观算法的改进就在于，在判断n是否为素数时不会遍历到n-1，而是遍历到$\sqrt{n}$即可，因为我们在找n的因数时，n分解为的两个因数一定是一个小于等于$\sqrt{n}$，一个大于等于$\sqrt{n}$，极端情况就是两个因数都为$\sqrt{n}$，如果一直到$\sqrt{n}$都不存在n的因数，那么之后也一定不会存在n的因数

时间复杂度：O(n$\sqrt{n}$)

代码实现

//从2到根号x遍历 
bool isPrime(int x)
{
	if(x==0||x==1)
		return false; 
	for(int i=2;i*i<=x;i++)
	{
		if(x%i==0)
			return false;
	} 
	return true;
}

埃氏筛法

前面讲的都是判断一个数是否为素数，后面的两种方法则是筛选出一定范围内的所有素数

埃氏筛比较简单，假设要筛选出从2到N中的所有素数，通过一个数组将从2到N中的所有数都标记为素数，然后遍历从2到N，如果遍历到的数是素数，那么就把这个数在范围内的所有倍数都标记为非素数即可

埃氏筛的原理就是当我们遍历到一个数的时候，如果从2到这个数中有它的因数，那么在之前这个数就一定会被筛选出去。如果这个数没有被筛选出去，那么在这中间它就没有因数，从而可以判断其为素数

时间复杂度：O(nloglogn)

代码实现

//埃氏筛
//遍历从2到N，如果vis为0则是素数，同时将该素数在N以内的所有倍数置vis为1 
const int N=100;//(筛选出1~100内的素数)
int prime[N+1];//保存素数
bool vis[N+1];//标记数组,vis=1表示不是素数 
int cnt=0;//保存素数个数 
void sieve()
{
	for(int i=2;i<=N;i++)
	{
		if(!vis[i])
		{
			prime[cnt++]=i;
			for(int j=2;i*j<=N;j++)
				vis[i*j]=1;
		} 
	}
	for(int i=0;i<cnt;i++)
		cout<<prime[i]<<" ";
	return;
} 

欧拉筛法

不知道大家有没有发现，在使用埃氏筛时有些数可能会被筛选多次，如12，它在i=2时会被26筛选一次，在i=3时又会被34筛选一次，这些重复的筛选影响了算法的执行效率
欧拉筛即针对这些重复的筛选进行了一个改进——对于每个合数只由它的最小质因数筛选一次

时间复杂度：O(n)

欧拉筛的原理较为复杂，我们先上代码，根据代码来讲解

//欧拉筛
//在使用埃氏筛筛选素数时有些计算会重复，比如2*3与3*2，将6标记了两遍
//欧拉筛的改进在于每个数只由它的最小素因数筛选一次
const int N=100;//(筛选出1~100内的素数)
int prime[N+1];//保存素数
bool vis[N+1];//标记数组,vis=1表示不是素数 
int cnt=0;//保存素数个数 
void sieve()
{
	for(int i=2;i<=N;i++)
	{
		if(!vis[i])
			prime[cnt++]=i;
		for(int j=0;j<cnt&&i*prime[j]<=N;j++)
		{
			vis[i*prime[j]]=1;
			if(i%prime[j]==0)
				break;
		}
	}
	for(int i=0;i<cnt;i++)
		cout<<prime[i]<<" ";
} 

变量的定义与埃氏筛相同，都是由vis来标记是否为素数，我们在这里重点关注内层循环

for(int j=0;j<cnt&&i*prime[j]<=N;j++)
{
	vis[i*prime[j]]=1;
	if(i%prime[j]==0)
		break;
}

这里是筛选出的是以prime[j]为最小素因子的合数，即prime[j]的i倍，这里筛选的顺序不太容易理解，我们先打一张表来详细看一下

注意这里，i为倍数，prime[j]为最小素因子
以2为最小素因子的合数会从i=2开始一直筛到最后

然后我们以i=7为例，筛选以7为最小素因子的数时我们是从i=7开始筛的，那么7的2,3,4,5,6倍我们不就没有筛吗？
实际上不是这样的，我们看i=7时prime[j]的值为2,3,5,7我们在筛选i*prime[j]时，实际上已经把小于7中的素数倍已经筛选出来了
那么7的合数倍(4,6)又是怎么筛选的呢？
以7*4为例我们可以将合数4分解为2*2，然后7*4就可以写成14*2，到这里我们就能看出来了，当i=14时我们就可以将14*2筛选出来了

---

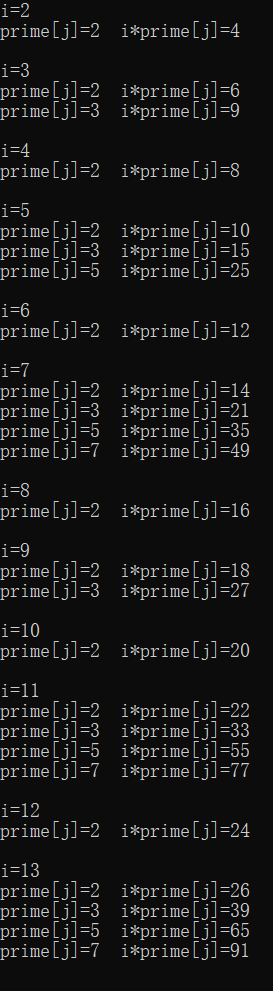
说完上面这些好像跟埃氏筛也没有什么不同嘛，好像并没有实现每个合数只会由它的最小素因数筛选一遍，别急，下面我们就要看欧拉筛中最最最关键的一段代码了，

if(i%prime[j]==0)
		break;

就是这一小段代码，就实现了只筛选一遍的改进，下面我们来分析这段代码
当i%prime[j]==0时，i就可以写成k*prime[j]的形式，此时如果我们不退出循环，继续执行，则下一次要筛选出的数为i*prime[j+1]，我们将i代换为k*prime[j]那么下次筛选的数就是k*prime[j+1]*prime[j]，而这里这个数的最小质因数实际上应该是prime[j]（prime是单调递增的），即应该由prime[j]筛掉而不是prime[j+1]，如果这一步筛掉的话，那么后面必然会由prime[j]再重复筛选一次
我们以i=4,prime[j]=2为例，这里筛选完之后因为4%2=0所以应该退出循环，我们假设其没有退出，继续筛选prime[j+1]=3此时筛掉的数字为4*3=12，12的最小质因数应该为2，那么当i=6，prime[j]=2时，12又会被筛选一次，这就导致了12的重复筛选

---

结语

关于素数筛的部分到这里就讲完啦，其中欧拉筛的实现原理有些复杂，上面写的也有些繁琐不到位的地方，欢迎大家在评论区提出建议，希望这篇文章能帮助到大家。