本博文来自维基上的矩阵计算:https://en.wikipedia.org/wiki/Matrix_calculus#Denominator-layout_notation
之前会发现在有的求导上最后结果需要转置,而有的不需要,很困惑,然后才发现了这个维基上面的解释(这才是写该博文的主要价值,注意到不同的布局问题,其他部分只是为了完整性而写的),而且下面也有很多很不错的参考链接,其中就有之前的矩阵计算(2)和矩阵计算(3)的链接。维基最后更新时间:17 April 2015, at 21:34.
matrix calculus
在数学上, 矩阵微积分是用来表示多变量的微积分,当然主要还是在矩阵空间上的。它覆盖了单一函数(单元)关于多变量的偏导,多变量函数(多元函数)关于单一变量、向量和矩阵的偏导(向量、矩阵可以被视为单一实体对待)。这种符号化的数学表示大大的简化了很多操作,例如查找多变量函数的最大值或者最小值,以及微分方程的求解系统等等。值得注意的是:下面使用的符号是在统计和工程领域中常用的,不过张量的指数表示(tensor index notation)是来自物理学。
不过有个我们之前未注意的是,有两派人它们使用着自己的符号约定,从而将矩阵微积分划分成了两个派别。这两个派别很容易区分,只要看它们写一个标量关于一个向量的导数是写成列向量还是行向量。不过这两个约定都是被大家所接受的,就算是在涉及到一般的矩阵计算的时候,将常规的向量默认视为列向量(而不是行向量)的情况下还是成立的。在矩阵微积分中,如果采取了一个约定,那么就使用该约定贯穿整个领域(例如:计量经济学,统计学,评估理论(etimation theory)和机器学习),不要混用不然会造成混乱。然而,在一个具体的领域中,不同的作者还是会使用不同的约定,因为会有来自不同派别的作者会将他们自己的约定作为标准。所以在没有去仔细的验证不同作者的资料的时候盲目的将他们的结论放在一起会有严重的错误。因而在一个完整的资料上需要确保符号的一致性。在下面的布局约定部分会有两种约定的定义介绍和比较。
一、范围
矩阵微积分指的是使用矩阵和向量来表示因变量每个成分关于自变量每个成分的导数。通常来说,自变量指的是标量、向量或者矩阵,而因变量指的是由自变量得到的结果。每种不同的情况会导致有不同规则集合(或者不同的微积分操作)。我们可以用有组织的矩阵符号来方便的表示不同的导数。
第一个例子,考虑向量微积分中的梯度。对于一个有着三个因变量的标量函数来说, 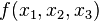 ,可以通过下面的向量方程来表示梯度:
,可以通过下面的向量方程来表示梯度:
这里  表示
表示  方向上的单元向量,其中
方向上的单元向量,其中 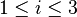 。该导数更广义的表示为:一个标量 f 关于一个向量
。该导数更广义的表示为:一个标量 f 关于一个向量 的导数,其结果的向量形式如下:
的导数,其结果的向量形式如下:
-
 [这不是通常的向量表示形式,通常的向量是表示成列向量]
[这不是通常的向量表示形式,通常的向量是表示成列向量]
更多复杂的例子,例如标量函数关于矩阵的导数,被称之为梯度矩阵,其中每个对应位置上的元素都是关于原始矩阵每个元素的导数。在这种情况下,一个标量(个人:也就是结果矩阵中的一个元素)就是矩阵中每个因变量的一个函数。另一个例子,如果我们有一个元素为因变量、函数、m个自变量的n维向量,我们就需要考虑因变量向量关于该自变量向量的导数。结果为表示所有可能导数组合的一个m×n 矩阵。当然,最多也就9种形式。如果我们在自变量和因变量中有更多层次的嵌套,那么组合数量就远远不止9种了。
下面表中就是以矩阵形式表示的常见的6种不同的导数形式。[1]
| 类型 | 标量 | 向量 | 矩阵 |
|---|---|---|---|
| 标量 | 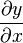 |
 |
 |
| 向量 |  |
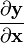 |
|
| 矩阵 | 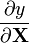 |
因为向量和标量都可以表示成简单的矩阵形式,所以这里我们使用“矩阵”来泛化的表示所有含义。而且,我们使用黑体字母来表示向量,而黑体大写字母表示矩阵。
当然上面的9个格子还少了几个组合,比如向量关于矩阵的导数等。不过,这些导数是以秩(rank)超过2的张量(tensor)表示的,所以它们不适合放在一个矩阵中。接下来的三个部分中,我们会这些导数,而且将他们与其他的数学分支联系起来。在下面的布局约定部分有更详细的表。
1.1 其他导数
矩阵导数这种符号可以很方便的用来表示微积分中的偏导数。Fréchet导数是泛函分析中求关于向量的导数的标准方式。在这种情况中,矩阵的矩阵函数是Fréchet可微分的,这两个派别的导数在符号的解释上是需要保持一致的。正如在一般的偏导数分析中,许多公式是在比现有的近似线性映射的导数下还弱的分析条件下扩展得到的。
1.2 用法
矩阵微积分可以用来计算最优随机估计(optimal stochastic estimators),通常会涉及到 拉格朗日乘子的使用。比如下面的几个例子:
二、符号
该小节的向量和矩阵导数遵循矩阵符号的规则,使用单个变量来表示一个包含着大量变量的实体。在该规则中,我们需要通过字体来区分标量,向量和矩阵。M(n,m)表示n行m列的实数矩阵空间。这样的矩阵以黑体大写字母表示:A, X, Y, etc.M(n,1)也就是一个列向量,表示成黑体小写字母:a, x, y, etc.M(1,1)也就是一个标量,表示成小写斜体字母:a, t, x, etc. XT 表示矩阵的转置, tr(X)表示迹,而det(X)表示的是行列式。所有的函数都假设是可微分类别 C1 的,除非有特别说明。字母表中上半部的普通的字母(a, b, c, …)用来表示常量,下半部字母(t, x, y, …)用来表示变量.
NOTE: 正如最开始说的,在向量和矩阵中关于偏导数的表示是不唯一的,因为没有一个完整的标准。下面两个介绍性的部分使用分子布局约定来简单的说下符号带来的便利,主要是为了避免过多的复杂讨论。在后面的布局约定中有更详细的介绍。我们应该注意到:
- 先不说"分子布局" 和"分母布局",其实还有其他的符号化解释。选择这两种的原因(或者在某些情况下,叫做分子布局,混合布局),是因为这样可以独立的解释标量关于向量, 向量关于标量,向量关于向量,和标量关于矩阵的导数,当然,有很多作者会以各种不同的方式来混用这些布局。
- 下面的介绍性部分使用分子布局,不代表这是“正确的”或者“优先”的选择。不同的布局类型都有优点和缺点。粗心的将不同的局部混合使用会导致很严重的错误,而且从一个布局转移到另一个布局也是需要谨慎对待的。所以,当在当前使用的公式中,最好的选择就是先验证使用的是什么布局,然后考虑遵循这个布局,不要试图在所有的情况下使用同一个布局(个人:就是如果你在推导一个公式,先了解该作者用的是什么布局,而不要以为所有的资料都是同一个布局。当然最好对每个公式都先验证下,这是为了防止有些作者在同一份资料中混乱的使用不同的布局)。
2.1 其他选择
使用爱因斯坦求和约定的张量指数表示(tensor index notation)非常像矩阵微积分,只是它是一次只有一个成分。它可以很轻松的对任意高秩的张量进行操作,因为秩超过2的张量不能够很好的通过矩阵符号来处理。这里所有的工作都可以以这种不使用单一变量的矩阵符号来完成。不过,在评估论和应用数学领域上,是需要对超多指数(indices)进行操作的,在这些领域中,矩阵微积分是很常见的。同样的,爱因斯坦符号可以作为通常的元素符号的替代方法,来表示这里的identities,不过当需要显式的求和的时候,这就变得很麻烦了。其实一个矩阵可以认为是有着秩为2的张量。(个人:该段的意思就是除了前两种表示法还有个张量指数表示法,具体的这里不介绍,可以看下面的参考文献。)
三、有关向量的导数
因为向量就是有着一列的矩阵。最简单的矩阵导数就是向量导数。
这里的符号可以用来表示一般的向量微积分操作,用欧式空间Rn中n维向量表示M(n,1),而实数空间R 实数表示M(1,1)。
NOTE:这里使用分子布局只是为了教学。有些作者还是会使用不同的约定的。下面的布局约定部分会有更详细的解释.
3.1 向量关于标量
在向量微积中,向量y 关于标量x 的导数被称为向量y 的目标向量,  。 注意:y:R
。 注意:y:R  Rm.
Rm.
Example;例如在欧式空间中,速率向量就是位置向量的目标向量(即关系到时间的函数)。同样,加速度也是速率的目标向量。
3.2 标量关于向量
标量y 关于向量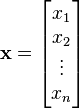 的导数的结果如下:(以分子布局约定)
的导数的结果如下:(以分子布局约定)
空间向量 x 的标量函数f(x)在单位向量 u上的方向导数定义成的梯度形式如下:
之前,标量关于向量的导数的符号可以重写成方向导数的形式: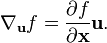 这种符号表示形式在乘积规则和链式规则的时候可以看起来和标量导数一样可读.
这种符号表示形式在乘积规则和链式规则的时候可以看起来和标量导数一样可读.
3.3 向量关于向量
之前的两种情况可以被认为是向量关于向量的导数的应用,只是其中某个向量的大小为1罢了。同样的,我们可以以同样的方式从向量推广到矩阵上。
向量函数(一个向量,其中的元素都是函数)  关于一个输入向量
关于一个输入向量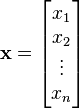 的导数可以写成如下形式:(分子布局约定)
的导数可以写成如下形式:(分子布局约定)
在向量微积分中,一个向量函数y 关于一个向量x(其成分被称之为一个空间)的导数被称之为pushforward或者differential, 或者是Jacobian矩阵.
在 Rm 中,pushforward即为向量函数f 关于向量v 的导数为:
四、关于矩阵的导数
有两种关于矩阵的导数类型,它们可以表示成大小相同的矩阵形式。即矩阵关于变量的导数和变量关于矩阵的导数。这在应用数学的许多领域中为了找到最小值问题是很有帮助的,它们可以被称之为:目标矩阵和梯度矩阵。
NOTE: 该部分使用分子布局约定也是出于教学目的。
4.1 矩阵关于标量
矩阵函数 Y 关于标量x 的导数被称之为 目标矩阵: (以分子布局约定)
4.2 标量关于矩阵
自变量为矩阵X 的标量函数 y 关于矩阵X的导数为:(分子布局约定)
注意到这里关于X的梯度的索引就是矩阵X索引的转置。(矩阵的标量函数会涉及到矩阵的迹和行列式)。
该导数也可以写成如下形式:
同样,矩阵 X 的标量函数f(X)在矩阵 Y的方向上的方向导数为:
这就是梯度矩阵,常用来解决评估论中的最小化问题,特别是在卡尔曼滤波的导数中占据着重要的地位。








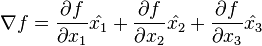
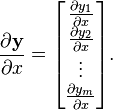
![\frac{\partial y}{\partial \mathbf{x}} =\left[\frac{\partial y}{\partial x_1} \ \ \frac{\partial y}{\partial x_2} \ \ \cdots \ \ \frac{\partial y}{\partial x_n}\right].](https://upload.wikimedia.org/math/7/f/5/7f52f0b5c0cd27fbeaccc76745c1a2a7.png)

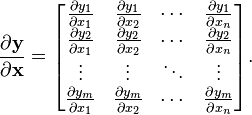
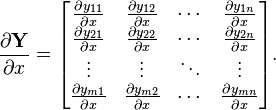
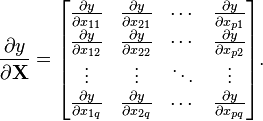



 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








