dx12 龙书第十七章学习笔记 -- 拾取

本文链接：https://blog.csdn.net/shuaigougou5545/article/details/127128428

本文介绍了一种3D拾取技术，主要讨论了如何确定用户通过鼠标指针所选择的3D物体。包括屏幕空间到投影窗口的变换、计算拾取射线、射线与网格的相交检测等内容。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本章讨论的问题是如何来确定用户通过鼠标指针所拾取的3D物体(或图元)。此时我们需要做一些逆于常规的事情,如何将特定的2D屏幕点变换回3D空间中。

假设我们点击了位于投影窗口中的点p对应于用户在屏幕上单击的点s,那么我们以观察点为起点,发出一条穿过点p的拾取射线(picking ray),则此射线会与投影中含有点p的物体相交。一旦计算出投影射线,我们就能遍历场景中的每一个物体,判断射线与之是否相交。再选取离摄像机最近且与射线相交的物体作为拾取对象。-- [这不就是光线追踪的原理嘛:>]

1.屏幕空间到投影窗口的变换

[设置视口在第4章(4.3.9)详细讨论过] -- 视口是窗口内的一部分

我们的首要任务是将用户在屏幕中点选的点变换为规格化设备坐标(Normalized Device Coordinates,NDC) -- [NDC在第5章(5.6.3.3)详细讨论过]。

视口变化：是将NDC坐标转换为显示屏幕坐标的过程：

$\\ x\in [-1,1],y\in [-1,1],z\in [0,1]\ \Rightarrow\ \\ x'\in [TopLeftX,TopLeftX+width],\\ y'\in[TopLeftY+height,TopLeftY],\\ z'\in [MinDepth,MaxDepth]$

注意：y坐标是反的！TopLeftX和TopLeftY这个是相对于Win32 API打开的窗口的左上角为基准！

假设屏幕宽度Width,高度Height,视口左上角坐标(TopLeftX,TopLeftY),我们只需要将坐标映射到新的区间上即可,因此我们可以构造如下👇矩阵完成映射操作：

$M=\begin{bmatrix} \frac{Width}{2} & 0 & 0 & 0\\ 0 & -\frac{Height}{2} &0 & 0 \\ 0 & 0 & MaxDepth-MinDepth & 0 \\ TopLeftX+\frac{Width}{2} & TopLeftY + \frac{Height}{2} & MinDepth & 1 \end{bmatrix}$

$[x',y',z',w']=[x,y,z,w]M$

视口矩阵中的变量可通过D3D12_VIEWPORT结构体来设置：

typedef struct D3D12_VIEWPORT {
    FLOAT TopLeftX;
    FLOAT TopLeftY;
    FLOAT Width;
    FLOAT Height;
    FLOAT MinDepth;
    FLOAT MaxDepth;
} D3D12_VIEWPORT;
 
// 在D3D中,存储在深度缓冲区中的数据都是0~1的归一化深度值
// MinDepth MaxDepth负责将深度值从[0~1]->[MinDepth,MaxDepth]
// 大多情况下通常会把MinDepth和MaxDepth分别设为0,1,也就是令深度值保持不变

一般来说,设置TopLeftX=0、TopLeftY=0、MinDepth=0、MaxDepth=1、Width=w以及Height=h,矩阵便可简化为：

$\begin{bmatrix} w/2 & 0 & 0 & 0 \\ 0 & -h/2 & 0 & 0\\ 0 & 0 & 1 & 0\\ w/2 & h/2 & 0 & 1 \end{bmatrix}$

将点从NDC空间变换到屏幕空间：

$[x_{ndc},y_{ndc},z_{ndc},1]\begin{bmatrix} w/2 & 0 & 0 & 0 \\ 0 & -h/2 & 0 & 0\\ 0 & 0 & 1 & 0\\ w/2 & h/2 & 0 & 1 \end{bmatrix}=[\frac{x_{ndc}w+w}{2},\frac{-y_{ndc}h+h}{2},z_{ndc},1]=[x_s,y_s,z_s,1]$

z_ndc仅会被深度缓冲区所用,这里就将其忽略,只考虑x和y坐标。

在拾取过程中,我们已知屏幕上的点 $[x_s,y_s,z_s,1]$ ,需要求出点 $p_{ndc}$ ：

$\\ x_{ndc}=\frac{2x_s}{w}-1 \\ y_{ndc}=-\frac{2y_s}{h}+1$

接下来将点从NDC空间转换到摄像机空间中的屏幕点：

①摄像机空间中平截头体：

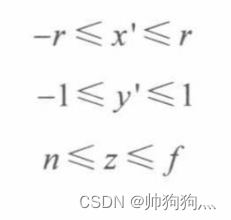
②NDC空间中：

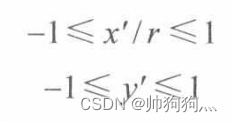
所以我们保持y坐标不变,将x乘上r即可,r是aspect ratio纵横比。

所以观察空间中xy坐标变为：

$\\ x_v=r(\frac{2x_s}{w}-1) \\ y_v=-(\frac{2y_s}{h}+1)$

这里的前提是我们定义摄像机空间中的投影窗口位于距原点d=cot(α/2)处,这里α为垂直视场角。我们定义该投影窗口长为2r,高为2。

因此摄像机空间中投影窗口内任意点坐标： $(x_v,y_v,d)$

为了方便计算斜率(且拾取射线都是同一条),我们通过相似三角形的方法计算出z=1处对应的坐标：

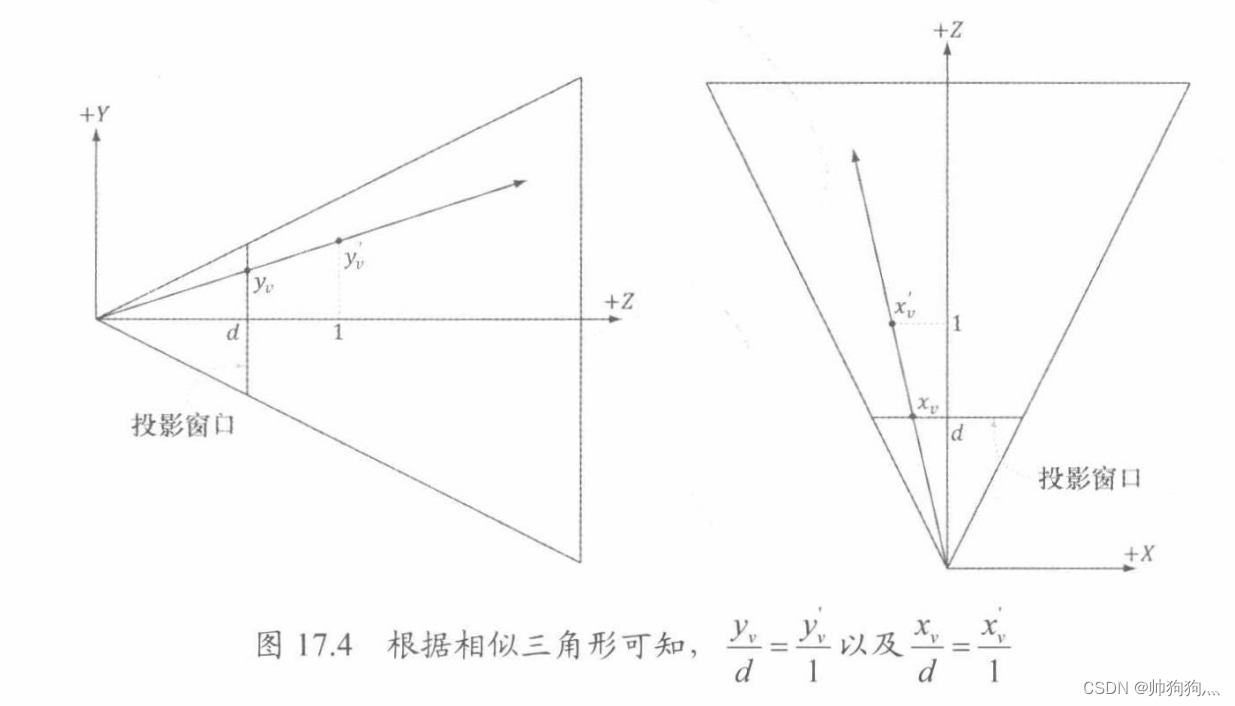
$\\ x_v'=\frac{x_v}{d}=(\frac{2x_s}{w}-1)rtan(\alpha/2) \\ y_v'=\frac{y_v}{d}=(-\frac{2y_s}{h}+1)tan(\alpha/2)$

由于投影矩阵： $p_{00} \ p_{11}$

所以上述x,y坐标可以改写成：

$\\ x_v'=\frac{(\frac{2x_s}{w}-1)}{p_{00}} \\ y_v'=\frac{(-\frac{2y_s}{h}+1)}{p_{11}}$

因此我们根据屏幕中点选的点 $(x_s,y_s)$ ,我们能计算出对应的拾取射线：

void PickingApp::Pick(int xs, int ys)
{
    XMFLOAT4X4 P = mCamera.GetProj4x4f();
    
    // 计算(x'_v,y'_v,d)
    float xv = (2.f*xs/mClientWidth-1.f)/P(0,0);
    float yv = (-2.f*ys/mClientHeight+1.f)/P(1,1);
    
    XMVECTOR rayOrigin = XMVectorSet(0.f, 0.f, 0.f, 1.f);
    XMVECTOR rayDir = XMVectorSet(xv, yv, 1.f, 0.f);
}

2.位于世界空间与局部空间中的拾取射线

我们可以通过观察矩阵的逆矩阵将拾取射线从摄像机空间转换到世界空间。假设V为观察矩阵,观察空间的拾取射线为 $r_v(t)=q+tu$ ,那么世界空间中的拾取射线为：

$r_w(t)=qV^{-1}+tuV^{-1}=q_w+tu_w$

但有时我们需要在局部空间中判断物体与射线的相交情况,所以将拾取射线从世界空间转换到局部空间,使用世界矩阵的逆矩阵：

$r_L(t)=q_wW^{-1}+tu_wW^{-1}$

为什么不把网格从局部空间转换到世界空间：因为网格中有上千顶点,代价十分高昂,不如直接转换拾取射线。

代码示例：将拾取射线从观察空间转换到物体的局部空间

mPickedRitem->Visible = false; // 最开始假设用户没有选择物体

// 检测用户是否拾取了一个不透明的渲染项
for(auto ri : mRitemLayer[(int)RenderLayer::Opaque])
{
    auto geo = ri->Geo;
    
    // 跳过不可见的渲染项 
    if(ri->Visible == false)
        continue;

    XMMATRIX V = mCamera.GetView();
    XMMATRIX invView = XMMatrixInverse(&XMMatrixDeterminant(V), V);
    
    XMMATRIX W = XMLoadFloat4x4(&ri->World);
    XMMATRIX invWorld = XMMatrixInverse(&XMMatrixDeterminant(W), W);

    // 将拾取射线变换到网格局部空间 
    XMMATRIX toLocal = XMMatrixMultiply(invView, invWorld);

    rayOrigin = XMVector3TransformCoord(rayOrigin, toLocal);
    rayDir = XMVector3TransformNormal(rayDir, toLocal);
    
    rayDir = XMVector3Normalize(rayDir); // 规范化
}

XMVector3TransformCoord与XMVector3TransformNormal都是执行矩阵乘法的函数,不同的是,前者会为结果的w赋1,后者会赋0,所以分别用来对点和向量进行变换(乘以变化矩阵)。

3.射线与网格的相交检测

拾取射线与网格一旦位于同一空间,我们就能通过相交检测来验证这两者是否相交。以下代码遍历网格中的所有三角形,并一一执行射线与三角形的相交检测：

// 首先判断拾取射线与网格的包围盒的关系,如果不相交,则射线也不可能与包围盒中的物体相交
float tmin = 0.f;
if(ri->Bounds.Intersects(rayOrigin, rayDir, tmin))
{
    // 对于不同格式混合在一起的顶点索引数据,我们需要使用元数据meshdata来执行强制类型转换
    // 这里我们使用网格几何体在系统内存(CPU)中的副本 -- 因为这里我们访问不到GPU资源
    auto vertices = (Vertex*)geo->VertexBufferCPU->GetBufferPointer();
    auto indices = (std::uint32_t*)geo->IndexBufferCPU->GetBufferPointer();
    UINT triCount = ri->IndexCount/3;
    
    tmin = MathHelper::Infinity;
    for(UINT i = 0; i < triCount; ++i)
    {
        UINT i0 = indices[i*3+0];
        UINT i1 = indices[i*3+1];
        UINT i2 = indices[i*3+2];

        XMVECTOR v0 = XMLoadFloat3(&vertices[i0].Pos);
        XMVECTOR v1 = XMLoadFloat3(&vertices[i1].Pos);
        XMVECTOR v2 = XMLoadFloat3(&vertices[i2].Pos);

        float t = 0.f;
        if(TriangleTests::Intersects(rayOrigin, rayDir, v0, v1, v2, t)) // t是引用传递
        {    
            if(t<tmin)
            {
                // 这是距离摄像机最近的一个被拾取的三角形
                tmin = t;
                UINT pickedTriangle = i;
                
                // 为被拾取的三角形设置渲染项,这样我们可以用高亮突出的材质来对他进行渲染
                mPickedRitem->Visible = true;
                mPickedRitem->IndexCount = 3;
                mPickedRitem->BaseVertexLocation = 0;

                mPickedRitem->World = ri->World;
                mPickedRitem->NumFramesDirty = gNumFrameResources;
                
                mPickedRitem->StartIndexLocation = 3 * pickedTriangle;
            }
        }      
    }
}

①射线与AABB的相交检测：

射线与包围盒相交的函数(DirectX碰撞检测库函数)：

bool XM_CALLCONV BoundingBox::Intersects(
    FXMVECTOR Origin, // 射线的端点 O
    FXMVECTOR Direction, // 射线的方向向量 d
    float& Dist // 射线的相交参数 -- t
) const;
// O+td

给定射线 $r(t)=q+tu$ 或者 $r(t)=o+td$ ,那么Dist参数输出的是相交点p对应的 $t_0$ 。

②射线与球体的相交检测：

bool XM_CALLCONV 
BoundingSphere::Intersects(
    FXMVECTOR Origin, 
    FXMVECTOR Direction, 
    float& Dist // 最小的正数t
) const;

③射线与三角形的相交检测：

bool XM_CALLCONV
TriangleTests::Intersects(
    FXMVECTOR Origin,
    FXMVECTOR Direction,
    FXMVECTOR V0, // 三角形顶点v0
    FXMVECTOR V1, // 三角形顶点v1
    HXMVECTOR V2, // 三角形顶点v2
    float& Dist
);

这里采用的是Möller Trumbore 算法,利用重心坐标表示三角形(所在平面)。

射线： $\mathbf{r}(t)=\mathbf{q}+t\mathbf{u}$