3 传输线理论
文章目录
参考教材:《微波技术与天线(第三版)》周希朗
参考课程:西北工业大学,微波技术与天线
传输线:以横电磁模(即TEM模)传输导行电磁波的传输系统。
分析方法:传输线的严格分析方法是“场”的分析方法,即根据麦克斯韦方程组和边界条件构成的边值问题解出所要求的电磁场。“场”的分析方法涉及包含三个空间变量和一个时间变量的求解,因此分析较为复杂。但在为了简化分析过程,对于较简单的传输线,我们通常采用“路”的分析方法,即仅涉及一个空间变量和一个时间变量的求解。
因此传输线理论可以简单理解为是使用“路”的分析方法(即关于使用一个空间变量和一个时间变量描述导行电磁波在传输线的传输过程的数学形式)分析导行电磁波在传输线的传输过程。
3.1 传输线的分布参数及其等效电路
相信大家在初中过程中都学过物理,在以初中物理的视角中,一根传输线(或称为导线)上传输的电流或电压是基本没有损耗的,可以说得上处处相等。也就是说我们通常认为沿线线的电压或电流只与源的输入有关,其幅度和相位均与在传输线上的位置无关。这是因为我们以前在线上传输的通常是低频的电压或电流(最常见的 50 H z 50Hz 50Hz 的市电),其传输的波长(波长:可以认为是一个周期信号以光速传播一个周期时间所经过的距离)与传输线的长度相比可以忽略不计,也就是我们可以认为低频信号还没怎么来得急变化就走完了这根传输线。
例如: 50 H z 50Hz 50Hz 的信号波长 λ ≈ 6000 K m \lambda\approx6000Km λ≈6000Km ,也就是说该信号完成一个周期的变化需要传输6000Km,然而我们家实际的传输线可能就100m左右,因此,我们可以忽略其在传输线上的变化,认为信号沿线的电压或电流只与时间有关,其幅度和相位均与在传输线上的位置均无关。
但是在微波领域中,我们所要传输的信号通常为 300 M H z 300MHz 300MHz(波长为 1 m 1m 1m)至 3000 3000 3000 G H z GHz GHz (波长为 0.1 0.1 0.1 m m mm mm),也就是说其波长与传输线上相当或更长,此时,信号在传输线上传输能完成大部分的周期变化甚至是多个周期变化。显然我们就不能忽略这种变化,因此认为信号沿线的电压或电流不仅只与时间有关,其幅度和相位还与其在传输线上的位置有关。
由此,我们将传输线划分为长线和短线。
短线:传输线的几何长度远小于线上传输导波的波长。短线对应于低频传输线,在低频电路中只起连接导线的作用。因其频率较低,分布参数所引起的效应可忽略不计,因此可认为沿线的电压或电流只与时间有关,其幅度和相位均与空间距离无关。
长线:传输线的几何长度与线上传输导波的波长相比拟或更长(一般认为几何长度为波长的 1 / 10 1/10 1/10 以上的为长线)。长线对应于微频传输系统,此时,传输线上的电压或电流不仅是时间的函数,同时是关于空间距离的函数。
如图3.1所示是我们微波领域中常用的几种传输线。

构建平行双导线的等效电路
下面我们进入描述传输线上电磁波变化的分析过程,首先进行分析时,我们假设这几种传输线结构周围或内部填充的媒质均为简单的电介质,即电参数均为 μ 0 , ε 0 , ε r , σ \mu_0,\varepsilon_0,\varepsilon_r,\sigma μ0,ε0,εr,σ ,且 σ \sigma σ 很小(介质损耗很小)。
下面以平行双导线为例,导出采用瞬时电压和瞬时电流表示的传输线方程:
假设均匀平行双导线满足以下条件:
- 导线的截面以及两导线间的间距比线上传输的导波的波长小得多,即只考虑 TEM 模传输,高次模式不存在;
- 两导线均为理想导体,导线间填充的介质为理想介质,即不考虑损耗;
- 线上导波的工作频率不是很高,既不考虑导波的辐射。
一般地,在均匀传输线上周围填充的是电导率 σ \sigma σ 的媒质,因此当高频信号通过传输线时将产生如下的分布参数效应:
- 因电流流过导线时引起导线发热而产生损耗,故其本身具有分布电阻效应;
- 因导线流过电流时其周围存在高频磁场,故其本身具有分布电感效应;
- 因导线间有电压,即导线间存在电场,故其本身具有分布电容效应;
- 若导线周围介质非理想绝缘,存在漏电流,故其本身具有分布电导效应;
因此当传输线通过高频信号时,这时传输线不能仅当成连接线分析,它将形成分布参数电路,其等效电路如 图 3.3 所示。

3.2 一般形式的传输线方程及其解
由 图3.1 我们可以得知平行双导线传输系统的等效电路,下面我们便可以对传输线上导波的传输特性进行分析。从一般形式的传输线方程出发,求解满足边界条件的瞬时电压和瞬时电流的波动方程或复电流和复电压满足的方程,从而导出传输线上的瞬时电压和瞬时电流或复电压和复电流。
3.2.1 一般形式的传输线方程
图 3.4 表示一均匀平行双导线传输系统。其中,传输线的始端接射频/微波信号源(简称信号源或波源),终端接负载,传输线的轴向坐标为 z z z ,坐标原点处于传输线的始端,来自波源的波沿正 z z z 方向传输。设波源的瞬时电动势为 e g e_g eg,内阻抗为 Z g Z_g Zg,负载阻抗为 Z l Z_l Zl;传输线上距始端为 z z z 处的瞬时电压、瞬时电流分别为 u ( z , t ) 、 i ( z , t ) u(z,t)、i(z,t) u(z,t)、i(z,t);在 z + Δ z z+\Delta z z+Δz 处的瞬时电压、瞬时电流分别为 u ( z + Δ z , t ) 、 i ( z + Δ z , t ) u(z+\Delta z,t)、i(z+\Delta z,t) u(z+Δz,t)、i(z+Δz,t)。
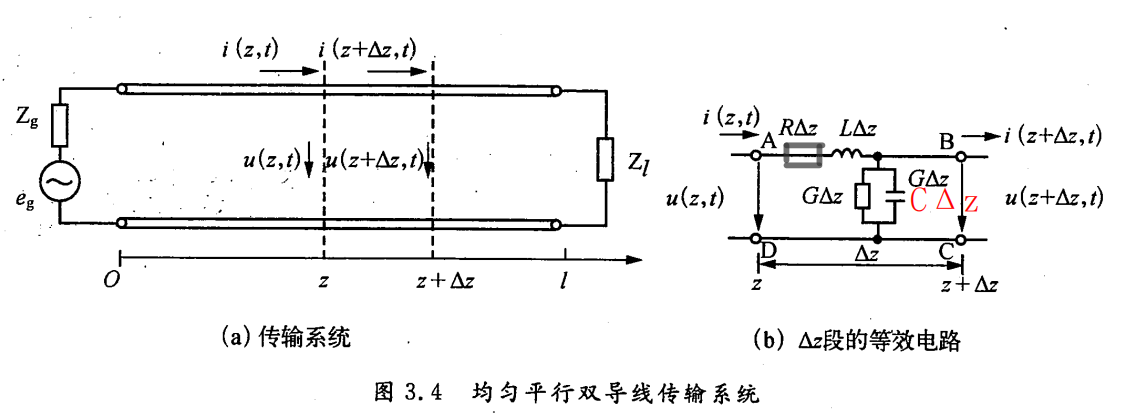
于是,参考图 3.4(b) 中
Δ
z
\Delta z
Δz 段的等效电路,沿回路 ABCD 应用基尔霍夫电压定律,可得
u
(
z
,
t
)
−
R
Δ
z
i
(
z
,
t
)
−
L
Δ
z
∂
i
(
z
,
t
)
∂
t
−
u
(
z
+
Δ
z
,
t
)
=
0
(3.9a)
u(z,t)-R\Delta z\,i(z,t)-L\Delta z\,\frac{\partial i(z,t)}{\partial t}- u(z+\Delta z,t)=0 \tag{3.9a}
u(z,t)−RΔzi(z,t)−LΔz∂t∂i(z,t)−u(z+Δz,t)=0(3.9a)
同样,对图 3.4(b) 中的节点 A 应用基尔霍夫电流定律,可得
i
(
z
,
t
)
−
G
Δ
z
u
(
z
,
t
)
−
C
Δ
z
∂
u
(
z
,
t
)
∂
t
−
i
(
z
+
Δ
z
,
t
)
=
0
(3.9b)
i(z,t)-G\Delta z\,u(z,t)-C\Delta z\,\frac{\partial u(z,t)}{\partial t}- i(z+\Delta z,t)=0 \tag{3.9b}
i(z,t)−GΔzu(z,t)−CΔz∂t∂u(z,t)−i(z+Δz,t)=0(3.9b)
令上两式中的
Δ
z
→
0
\Delta z \to 0
Δz→0,取极限,即可得
∂
u
(
z
,
t
)
∂
z
=
−
R
i
(
z
,
t
)
−
L
∂
i
(
z
,
t
)
∂
t
∂
i
(
z
,
t
)
∂
z
=
−
G
u
(
z
,
t
)
−
C
∂
u
(
z
,
t
)
∂
t
\begin{align} \frac{\partial u(z,t)}{\partial z}=-Ri(z,t)-L\frac{\partial i(z,t)}{\partial t} \tag{3.9c}\\ \frac{\partial i(z,t)}{\partial z}=-Gu(z,t)-C\frac{\partial u(z,t)}{\partial t} \tag{3.9d} \end{align}
∂z∂u(z,t)=−Ri(z,t)−L∂t∂i(z,t)∂z∂i(z,t)=−Gu(z,t)−C∂t∂u(z,t)(3.9c)(3.9d)
由上可得一般形式的传输线方程。
对于无耗传输线,此时
R
=
0
,
G
=
0
R=0,G=0
R=0,G=0 ,上式简化为
∂
u
(
z
,
t
)
∂
z
=
−
L
∂
i
(
z
,
t
)
∂
t
∂
i
(
z
,
t
)
∂
z
=
−
C
∂
u
(
z
,
t
)
∂
t
\begin{align} \frac{\partial u(z,t)}{\partial z}=-L\frac{\partial i(z,t)}{\partial t} \tag{3.10a}\\ \frac{\partial i(z,t)}{\partial z}=-C\frac{\partial u(z,t)}{\partial t} \tag{3.10b} \end{align}
∂z∂u(z,t)=−L∂t∂i(z,t)∂z∂i(z,t)=−C∂t∂u(z,t)(3.10a)(3.10b)
联立二式可得
∂
2
u
(
z
,
t
)
∂
z
2
=
L
C
∂
2
u
(
z
,
t
)
∂
t
2
∂
2
i
(
z
,
t
)
∂
z
2
=
L
C
∂
2
i
(
z
,
t
)
∂
t
2
\begin{align} \frac{\partial^2 u(z,t)}{\partial z^2}=LC\frac{\partial^2 u(z,t)}{\partial t^2} \tag{3.11a}\\ \frac{\partial^2 i(z,t)}{\partial z^2}=LC\frac{\partial^2 i(z,t)}{\partial t^2} \tag{3.11b} \end{align}
∂z2∂2u(z,t)=LC∂t2∂2u(z,t)∂z2∂2i(z,t)=LC∂t2∂2i(z,t)(3.11a)(3.11b)
由此得无耗传输线上瞬时电压和瞬时电流所满足得一组齐次波动方程,求解该方程可得到沿线电压波和电流波的传播特性。
事实上,传输线上的电压和电流一般作时谐变化。此时,我们可以通过采用复数形式表示来简化分析(降元)。为此,令
u
(
z
,
t
)
=
Re
[
U
˙
(
z
)
e
j
ω
t
]
=
简记为
Re
[
U
(
z
)
e
j
ω
t
]
i
(
z
,
t
)
=
Re
[
I
˙
(
z
)
e
j
ω
t
]
=
简记为
Re
[
I
(
z
)
e
j
ω
t
]
(3.13)
\begin{align} u(z,t)=\text{Re}[\dot{U}(z)e^{j\omega t}]\xlongequal{简记为} \text{Re}[U(z)e^{j\omega t}]\\ i(z,t)=\text{Re}[\dot{I}(z)e^{j\omega t}]\xlongequal{简记为} \text{Re}[I(z)e^{j\omega t}] \end{align}\tag{3.13}
u(z,t)=Re[U˙(z)ejωt]简记为Re[U(z)ejωt]i(z,t)=Re[I˙(z)ejωt]简记为Re[I(z)ejωt](3.13)
式中,
U
(
z
)
,
I
(
z
)
U(z),I(z)
U(z),I(z) 分别是传输线上
z
z
z 处的复电压和复电流(或简称为电压和电流),它们仅是坐标
z
z
z 的函数,转换为复电压和复电流,得
d
U
(
z
)
d
z
=
−
Z
I
(
z
)
d
I
(
z
)
d
z
=
−
Y
U
(
z
)
\begin{align} \frac{d U(z)}{dz}=-ZI(z)\tag{3.14a}\\ \frac{d I(z)}{dz}=-YU(z)\tag{3.14b} \end{align}
dzdU(z)=−ZI(z)dzdI(z)=−YU(z)(3.14a)(3.14b)
式中,
Z
=
R
+
j
ω
L
Z=R+j\omega L
Z=R+jωL,为传输线单位长度得串联阻抗;
Y
=
G
+
j
ω
C
Y=G+j\omega C
Y=G+jωC,为传输线单位长度得并联导纳。
3.2.2 均匀传输线方程的解
从3.2.1我们得到了均匀传输线的方程,下面进行方程的求解。联立 式(3.14a)和(3.14b),可得
d
2
U
(
z
)
d
z
2
−
Z
Y
U
(
z
)
=
0
d
2
I
(
z
)
d
z
2
−
Z
Y
I
(
z
)
=
0
\begin{align} \frac{d^2 U(z)}{dz^2}-ZYU(z)=0 \tag{3.15a}\\\\ \frac{d^2 I(z)}{dz^2}-ZYI(z)=0 \tag{3.15b} \end{align}
dz2d2U(z)−ZYU(z)=0dz2d2I(z)−ZYI(z)=0(3.15a)(3.15b)
令
γ
2
=
Z
Y
=
(
R
+
j
ω
L
)
(
G
+
j
ω
C
)
\gamma^2=ZY=(R+j\omega L)(G+j\omega C)
γ2=ZY=(R+jωL)(G+jωC),则以上两式可写为
d
2
U
(
z
)
d
z
2
−
γ
2
U
(
z
)
=
0
d
2
I
(
z
)
d
z
2
−
γ
2
I
(
z
)
=
0
\begin{align} \frac{d^2 U(z)}{dz^2}-\gamma^2 U(z)=0 \tag{3.16a}\\\\ \frac{d^2 I(z)}{dz^2}-\gamma^2 I(z)=0 \tag{3.16b} \end{align}
dz2d2U(z)−γ2U(z)=0dz2d2I(z)−γ2I(z)=0(3.16a)(3.16b)
式(3.16)上式为二阶齐次常微分方程,则其通解有
U
(
z
)
=
U
+
e
−
γ
z
+
U
−
e
γ
z
=
U
+
(
z
)
+
U
−
(
z
)
I
(
z
)
=
I
+
e
−
γ
z
+
I
−
e
γ
z
=
I
+
(
z
)
+
I
−
(
z
)
\begin{align} U(z)&=U^+ e^{-\gamma z}+U^- e^{\gamma z}=U^+ (z)+U^- (z) \tag{3.17a}\\\\ I(z)&=I^+ e^{-\gamma z}+I^- e^{\gamma z}=I^+ (z)+I^- (z) \tag{3.17b} \end{align}
U(z)I(z)=U+e−γz+U−eγz=U+(z)+U−(z)=I+e−γz+I−eγz=I+(z)+I−(z)(3.17a)(3.17b)
式中常数
U
+
,
U
−
,
I
+
,
I
−
U^+,U^-,I^+,I^-
U+,U−,I+,I− 由边界条件确定,而
Z
0
=
1
Y
0
=
Z
Y
=
R
+
j
ω
L
G
+
j
ω
C
γ
=
Z
Y
=
[
(
R
+
j
ω
L
)
(
G
+
j
ω
C
)
]
1
2
=
α
+
j
β
\begin{align} Z_0&=\frac{1}{Y_0}=\sqrt{\frac{Z}{Y}}= \sqrt{\frac{R+j\omega L}{G+j\omega C}} \tag{3.18}\\\\ \gamma&=\sqrt{ZY}=[(R+j\omega L)(G+j\omega C)]^{\frac{1}{2}}= \alpha+j\beta \tag{3.19} \end{align}
Z0γ=Y01=YZ=G+jωCR+jωL=ZY=[(R+jωL)(G+jωC)]21=α+jβ(3.18)(3.19)
因
Z
0
Z_0
Z0 有阻抗的量纲,且仅与分布参数有关,故称其为传输线的特性阻抗,而
Y
0
Y_0
Y0 称为传输线的特性导纳。
将 γ \gamma γ 定义为传播常数,用来衡量波随传播距离的变化,其通常为复数,其实部 α \alpha α 为衰减常数,单位为 Np/m \text{Np/m} Np/m;其虚部 β \beta β 为相移常数,单位为 rad/m \text{rad/m} rad/m。
设
U
+
=
∣
U
+
∣
e
j
φ
+
,
U
−
=
∣
U
−
∣
e
j
φ
−
,
Z
0
=
∣
Z
0
∣
e
j
φ
0
U^+=|U^+|e^{j\varphi_+},U^-=|U^-|e^{j\varphi_-},Z_0=|Z_0|e^{j\varphi_0}
U+=∣U+∣ejφ+,U−=∣U−∣ejφ−,Z0=∣Z0∣ejφ0,将式(3.17)代入式(3.13),即可得传输线上电压、电流的瞬时值的表达式为
U
(
z
,
t
)
=
∣
U
+
∣
e
−
α
z
cos
(
ω
t
−
β
z
+
φ
+
)
+
∣
U
−
∣
e
α
z
cos
(
ω
t
+
β
z
+
φ
−
)
=
u
+
(
z
,
t
)
+
u
−
(
z
,
t
)
I
(
z
,
t
)
=
1
∣
Z
0
∣
[
∣
U
+
∣
e
−
α
z
cos
(
ω
t
−
β
z
+
ψ
+
)
−
∣
U
−
∣
e
α
z
cos
(
ω
t
+
β
z
+
ψ
−
)
]
=
i
+
(
z
,
t
)
+
i
−
(
z
,
t
)
(3.20)
\begin{align} U(z,t)&=|U^+|e^{-\alpha z}\cos(\omega t-\beta z+\varphi_+)+ |U^-|e^{\alpha z}\cos(\omega t+\beta z+\varphi_-)\\ &=u^+(z,t)+u^-(z,t) \\ I(z,t)&=\frac{1}{|Z_0|}[|U^+|e^{-\alpha z}\cos(\omega t-\beta z+\psi_+)- |U^-|e^{\alpha z}\cos(\omega t+\beta z+\psi_-)]\\ &=i^+(z,t)+i^-(z,t) \end{align}\tag{3.20}
U(z,t)I(z,t)=∣U+∣e−αzcos(ωt−βz+φ+)+∣U−∣eαzcos(ωt+βz+φ−)=u+(z,t)+u−(z,t)=∣Z0∣1[∣U+∣e−αzcos(ωt−βz+ψ+)−∣U−∣eαzcos(ωt+βz+ψ−)]=i+(z,t)+i−(z,t)(3.20)
式中,
ψ
+
=
φ
+
+
φ
0
,
ψ
−
=
φ
−
+
φ
0
\psi_+=\varphi_++\varphi_0,\psi_-=\varphi_-+\varphi_0
ψ+=φ++φ0,ψ−=φ−+φ0。
由(3.20)可见,传输线上的电压、电流以波的形式传播,其上任一点 z z z 处的电压、电流均包含两部分:
- 第一项代表由波源向负载方向传播的行波,称为入射波,其振幅沿 z z z 方向呈指数规律减小,且相位连续滞后;
- 第二项代表由负载向波源方向传播的行波,称为反射波,其振幅沿 − z -z −z 方向呈指数规律减小,且相位连续滞后;
因此,传输线上任一点的电压、电流波通常都是由入射波和反射波的电压、电流叠加而成。
我们已经求得了传输线上电压、电流波的表达式,但其常数 U + , U − , I + , I − U^+,U^-,I^+,I^- U+,U−,I+,I− 还没确定,下面根据边界条件确定常数 U + , U − , I + , I − U^+,U^-,I^+,I^- U+,U−,I+,I−。图 3.5 展示了典型的由时谐电压源馈电的传输线系统。由图可知,传输线的边界条件通常有以下三种:
-
已知始端电压 U i U_i Ui 和电流 I i I_i Ii;
U + = 1 2 ( U i + I i Z 0 ) , U − = 1 2 ( U i − I i Z 0 ) (3.21) U^+=\frac{1}{2}(U_i+I_iZ_0),\\U^-=\frac{1}{2}(U_i-I_iZ_0) \tag{3.21} U+=21(Ui+IiZ0),U−=21(Ui−IiZ0)(3.21) -
已知终端电压 U l U_l Ul 和电流 I l I_l Il;
U l = U + e − γ l + U − e γ l , I l = 1 Z 0 ( U + e − γ l − U − e γ l ) (3.23) U_l=U^+e^{-\gamma l}+U^-e^{\gamma l},\\ I_l=\frac{1}{Z_0}(U^+e^{-\gamma l}-U^-e^{\gamma l}) \tag{3.23} Ul=U+e−γl+U−eγl,Il=Z01(U+e−γl−U−eγl)(3.23)
由此解得 U + U^+ U+ 和 U − U^- U−,代入 式(3.20)可得
U ( z ′ ) = U l cosh γ z ′ + I l Z 0 sinh γ z ′ I ( z ′ ) = I l cosh γ z ′ + U l Z 0 sinh γ z ′ \begin{align} U(z')&=U_l\cosh \gamma z'+I_lZ_0\sinh \gamma z'\tag{3.26a}\\ I(z')&=I_l\cosh \gamma z'+\frac{U_l}{Z_0} \sinh \gamma z'\tag{3.26b}\\ \end{align} U(z′)I(z′)=Ulcoshγz′+IlZ0sinhγz′=Ilcoshγz′+Z0Ulsinhγz′(3.26a)(3.26b)
式中, U l = U ′ + U ′ − , I l = ( U ′ + U ′ − ) / Z 0 U_l=U'^+U'^-,I_l=(U'^+U'^-)/Z_0 Ul=U′+U′−,Il=(U′+U′−)/Z0。若传输线无耗,即 γ = j β \gamma=j\beta γ=jβ ,此时并将 Z 0 Z_0 Z0 改为 Z c Z_c Zc ,则式(3.26)变为
U ( z ′ ) = U l cos β z ′ + j I l Z c sin β z ′ I ( z ′ ) = I l cos β z ′ + j U l Z c sin β z ′ \begin{align} U(z')&=U_l\cos \beta z'+jI_lZ_c\sin \beta z'\tag{3.27a}\\ I(z')&=I_l\cos \beta z'+j\frac{U_l}{Z_c} \sin \beta z'\tag{3.27b}\\ \end{align} U(z′)I(z′)=Ulcosβz′+jIlZcsinβz′=Ilcosβz′+jZcUlsinβz′(3.27a)(3.27b) -
已知波源(复)电动势 E g E_g Eg、内阻抗 Z g Z_g Zg 以及负载阻抗 Z l Z_l Zl。

求得 U + , U − , I + , I − U^+,U^-,I^+,I^- U+,U−,I+,I− 后代入(3.17)即可,若传输线无耗,即 γ = j β \gamma=j\beta γ=jβ ,此时并将 Z 0 Z_0 Z0 改为 Z c Z_c Zc 即可。
3.2.3 传输线的等效电路参数和工作特性参量
通过上一节的分析,我们可以总结出传输线的几个重要参数。
1. 等效电路参数
| 分布参数 | 平行双导线 | 同轴线 | 平行导体板 |
|---|---|---|---|
| R ( Ω / m ) R(\Omega/\text m) R(Ω/m) | R s π a \frac{R_s}{\pi a} πaRs | R s 2 π ( 1 a + 1 b ) \frac{R_s}{2\pi}(\frac1{a}+\frac1{b}) 2πRs(a1+b1) | 2 R s W \frac{2R_s}{W} W2Rs |
| L ( H/m ) L(\text{H/m}) L(H/m) | μ π ln [ ( D 2 a ) + ( D 2 a ) 2 − 1 ] \frac\mu\pi\ln\bigg[(\frac D{2a})+\sqrt{(\frac D{2a})^2-1} \bigg] πμln[(2aD)+(2aD)2−1] | μ π ln ( b a ) \frac\mu\pi\ln(\frac ba) πμln(ab) | μ b W \frac{\mu b}W Wμb |
| G ( S/m ) G(\text{S/m}) G(S/m) | π σ ln [ ( D 2 a ) + ( D 2 a ) 2 − 1 ] \frac{\pi\sigma}{\ln\bigg[(\frac D{2a})+\sqrt{(\frac D{2a})^2-1} \bigg]} ln[(2aD)+(2aD)2−1]πσ | 2 π σ ln ( b a ) \frac{2\pi\sigma}{\ln(\frac ba)} ln(ab)2πσ | σ W b \frac{\sigma W}b bσW |
| C ( F/m ) C(\text{F/m}) C(F/m) | π ε ln [ ( D 2 a ) + ( D 2 a ) 2 − 1 ] \frac{\pi\varepsilon}{\ln\bigg[(\frac D{2a})+\sqrt{(\frac D{2a})^2-1} \bigg]} ln[(2aD)+(2aD)2−1]πε | 2 π ε ln ( b a ) \frac{2\pi\varepsilon}{\ln(\frac ba)} ln(ab)2πε | ε W b \frac{\varepsilon W}b bεW |
注: R s = π f μ c / σ c R_s=\sqrt{\pi f\mu_c/\sigma_c} Rs=πfμc/σc, μ c , σ c \mu_c,\sigma_c μc,σc 为导体的磁导率和电导率; ε , μ , σ \varepsilon,\mu,\sigma ε,μ,σ 为导体周围空间填充媒质的介电常数、磁导率以及电导率。
2. 特性阻抗
TEM 模传输线的特性阻抗等于入射波电压与入射波电流之比,或反射波电压与反射波电流之比的负值。则有
Z
0
=
U
+
(
z
)
I
+
(
z
)
=
−
U
−
(
z
)
I
−
(
z
)
(
Ω
)
(3.34)
Z_0=\frac{U^+(z)}{I^+(z)}=-\frac{U^-(z)}{I^-(z)} (\Omega) \tag{3.34}
Z0=I+(z)U+(z)=−I−(z)U−(z)(Ω)(3.34)
这表明,若传输线延伸至无穷远处,则传输线上任一点处的入射波的复电压与复电流之比一定为常数(即为传输线的特性阻抗)。
由 式(3.18)可知:
-
直流情况 ( ω = 0 \omega=0 ω=0), Z 0 ( ω = 0 ) = R / G Z_0(\omega=0)=\sqrt{R/G} Z0(ω=0)=R/G ;
-
ω → ∞ \omega\to\infty ω→∞ , Z 0 ( ω → ∞ ) = L / C Z_0(\omega\to\infty)=\sqrt{L/C} Z0(ω→∞)=L/C ;
-
对于无耗传输线( R = 0 , G = 0 R=0,G=0 R=0,G=0),则特性阻抗 Z c Z_c Zc 为
Z c = Z Y = L C (3.35) Z_c=\sqrt\frac{Z}{Y}=\sqrt\frac{L}{C} \tag{3.35} Zc=YZ=CL(3.35)
此时, Z c Z_c Zc 为实数值。 -
在微波波段,一般有 R ≪ ω L , G ≪ ω C R\ll\omega L,G\ll\omega C R≪ωL,G≪ωC,即传输线损耗很小,此时根号因子均取二项式级数展开式的前两项作为近似,则有
Z 0 = R + j ω L G + j ω C ≈ L C [ 1 + j 2 ω ( G C − R L ) ] ≈ L C = Z c (3.36) Z_0=\sqrt{\frac{R+j\omega L}{G+j\omega C}}\approx\sqrt\frac{L}{C} \bigg[1+\frac{j}{2\omega}(\frac{G}{C}-\frac{R}{L})\bigg] \approx\sqrt\frac{L}{C} =Z_c\tag{3.36} Z0=G+jωCR+jωL≈CL[1+2ωj(CG−LR)]≈CL=Zc(3.36)
注:二项式级数展开式为
(
1
+
x
)
n
=
1
+
n
x
+
n
(
n
−
1
)
2
!
x
2
+
⋯
+
n
!
(
n
−
r
)
!
r
!
x
r
+
⋯
(1+x)^n=1+nx+\frac{n(n-1)}{2!}x^2+\cdots+\frac{n!}{(n-r)!r!}x^r+\cdots
(1+x)n=1+nx+2!n(n−1)x2+⋯+(n−r)!r!n!xr+⋯
常见传输线的特性阻抗
由表3.1 和图3.1可知
-
半径为 2 a 2a 2a 、间距为 D D D 无耗平行双导线的特性阻表达式为
Z c = 120 ε r ln [ D 2 a + ( D 2 a ) 2 − 1 ] ( Ω ) (3.37) Z_c=\frac{120}{\sqrt{\varepsilon_r}}\ln \bigg[ \frac{D}{2a}+\sqrt{(\frac{D}{2a})^2-1} \bigg]\,\,\,(\Omega) \tag{3.37} Zc=εr120ln[2aD+(2aD)2−1](Ω)(3.37)
实际中,常用特性阻抗为 300 Ω , 400 Ω , 600 Ω 300\Omega,400\Omega,600\Omega 300Ω,400Ω,600Ω 的平行双导线。 -
内、外导体半径分别为 a a a 和 b b b 的无耗同轴线的特性阻抗的表达式为
Z c = 60 ε r ln ( b a ) ( Ω ) (3.38) Z_c=\frac{60}{\sqrt{\varepsilon_r}}\ln(\frac{b}{a})\,\,\,(\Omega) \tag{3.38} Zc=εr60ln(ab)(Ω)(3.38)
实际中,常用特性阻抗为 50 Ω , 75 Ω 50\Omega,75\Omega 50Ω,75Ω 的同轴线。 -
宽为 W W W ,两板间距为 b b b 的无耗平行导体板
Z c = 120 π b W ε r ( Ω ) (3.39) Z_c=\frac{120\pi b}{W\sqrt{\varepsilon_r}}\,\,\,(\Omega)\tag{3.39} Zc=Wεr120πb(Ω)(3.39)
例如,对内、外直径分别为 2 a = 0.9144 m m , 2 b = 3.0226 m m 2a=0.9144mm,2b=3.0226mm 2a=0.9144mm,2b=3.0226mm 的铜质同轴线,若内外导体之间填充相对介电常数 ε r = 2.1 \varepsilon_r=2.1 εr=2.1 的无耗聚四氟乙烯,则其单位长度的分布电容、单位长度的分布电感分别为 C = 97.71 pF/m C=97.71\text{pF/m} C=97.71pF/m , L = 239.12 nH/m L=239.12\text{nH/m} L=239.12nH/m ,其特性阻抗 Z c = 49.50 Ω Z_c=49.50\Omega Zc=49.50Ω 。此外,取铜的电导率为 σ = 5.8 × 1 0 7 S/m \sigma=5.8\times10^7\text{S/m} σ=5.8×107S/m ,若聚四氟乙烯的损耗角正切为 1.5 × 1 0 − 4 1.5\times 10^{-4} 1.5×10−4 ,且同轴线的工作频率为 1 GHz 1\text{GHz} 1GHz ,则有耗同轴线的特性阻抗为 Z 0 = 49.50 − j 0.058 Ω Z_0=49.50-j0.058\Omega Z0=49.50−j0.058Ω,其值无限接近于无耗同轴线的特性阻抗值。
3. 传播常数
传播常数是描述时谐信号在传输线上变化的参数。
对于无耗传输线,
R
=
G
=
0
R=G=0
R=G=0,由式(3.19)可得
γ
=
j
ω
L
C
或
α
=
0
,
β
=
ω
L
C
(3.40)
\gamma=j\omega\sqrt{LC} \hspace{1em}或\hspace{1em}\alpha=0,\beta=\omega\sqrt{LC} \tag{3.40}
γ=jωLC或α=0,β=ωLC(3.40)
对于有耗传输线,传播常数
γ
=
α
+
j
β
=
(
R
+
j
ω
L
)
(
G
+
j
ω
C
)
\gamma=\alpha+j\beta=\sqrt{(R+j\omega L)(G+j\omega C)}
γ=α+jβ=(R+jωL)(G+jωC),则有
α
=
1
2
[
(
R
G
−
ω
2
L
C
)
+
(
R
2
+
ω
2
L
2
)
(
G
2
+
ω
2
C
2
)
]
β
=
1
2
[
(
ω
2
L
C
−
R
G
)
+
(
R
2
+
ω
2
L
2
)
(
G
2
+
ω
2
C
2
)
]
\alpha=\sqrt{\frac{1}{2}\big[ (RG-\omega^2LC)+\sqrt{(R^2+\omega^2L^2)(G^2+\omega^2C^2)} \big]}\\ \beta=\sqrt{\frac{1}{2}\big[ (\omega^2LC-RG)+\sqrt{(R^2+\omega^2L^2)(G^2+\omega^2C^2)} \big]}\\
α=21[(RG−ω2LC)+(R2+ω2L2)(G2+ω2C2)]β=21[(ω2LC−RG)+(R2+ω2L2)(G2+ω2C2)]
在射频/微波波段,
R
≪
ω
L
,
G
≪
ω
C
R\ll\omega L,G\ll\omega C
R≪ωL,G≪ωC,则有
γ
≈
j
ω
L
C
(
1
−
j
R
2
ω
L
)
(
1
−
j
G
2
ω
C
)
≈
1
2
(
R
Y
c
+
G
Z
c
)
+
j
ω
L
C
(3.41)
\gamma\approx j\omega\sqrt{LC}(1-j\frac{R}{2\omega L})(1-j\frac{G}{2\omega C}) \approx\frac{1}{2}(RY_c+GZ_c)+j\omega \sqrt{LC}\tag{3.41}
γ≈jωLC(1−j2ωLR)(1−j2ωCG)≈21(RYc+GZc)+jωLC(3.41)
β ≈ ω L C ( rad/m ) (3.42) \beta\approx\omega \sqrt{LC} \hspace{1em} (\text{rad/m})\tag{3.42} β≈ωLC(rad/m)(3.42)
α ≈ 1 2 ( R Y c + G Z c ) ( Np/m ) (3.42) \alpha\approx\frac{1}{2}(RY_c+GZ_c) \hspace{1em} (\text{Np/m})\tag{3.42} α≈21(RYc+GZc)(Np/m)(3.42)
4. 相速与波长
1)相速
相速即传输线上导波相位的变化速度,可表示为
v
p
=
ω
β
(
m/s
)
(3.44)
v_p=\frac{\omega}{\beta}\hspace{1em}(\text{m/s}) \tag{3.44}
vp=βω(m/s)(3.44)
2)波长
波长是指波在一个振动周期内传播的距离,故传输线上传输的导波(TEM波)的波长
λ
\lambda
λ 可表示为
λ
=
2
π
β
=
v
p
f
=
c
f
ε
r
=
λ
0
ε
r
(
m
)
(3.45)
\lambda=\frac{2\pi}{\beta}=\frac{v_p}{f}= \frac{c}{f\sqrt{\varepsilon_r}}=\frac{\lambda_0}{\varepsilon_r} \hspace{1em}(\text{m}) \tag{3.45}
λ=β2π=fvp=fεrc=εrλ0(m)(3.45)
式中,假设传输线周围填充的媒质是理想的简单介质,而
λ
0
=
c
/
f
\lambda_0=c/f
λ0=c/f 为真空中的波长,又称为工作波长。
注:对于无耗传输线,由式(3.42)和(3.44)可知,相速 v p v_p vp 与工作频率无关,为一常数,此时传输线上传输的导波为非色散波。这意味着传输线输入端输入一个对时间作任意变化的信号,此信号在传输过程中不会产生波形畸变。事实上,传输线上总存在一定损耗,此时相位(移)常数不再是 ω \omega ω 的线性函数,他将使 v p v_p vp 与频率有关。因此发生色散现象,传输过程中波形失真也是不可避免的。
























 3939
3939

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








