【数据结构】拓扑排序

设G=(V, E)是一个具有n个顶点的有向图，V中的顶点序列v0,v1,v2,…,vn-1如果满足下列条件：若从vi到vj有一条路径，则在顶点序列中顶点vi必定在vj之前，这样的序列称为拓扑序列。对一个有向图构造拓扑序列的过程称为拓扑排序(topological sort)。

显然，每一个可以构造出不止一个拓扑序列。

拓扑排序的步骤如下：1、在有向图中选一个没有前驱的顶点并输出；2、从图中删除该顶点和所有以它为尾的弧。
重复以上两个步骤，直至全部顶点均已输出，或者当前图中不存在无前驱的顶点为止。后一种情况说明有向图中存在环。
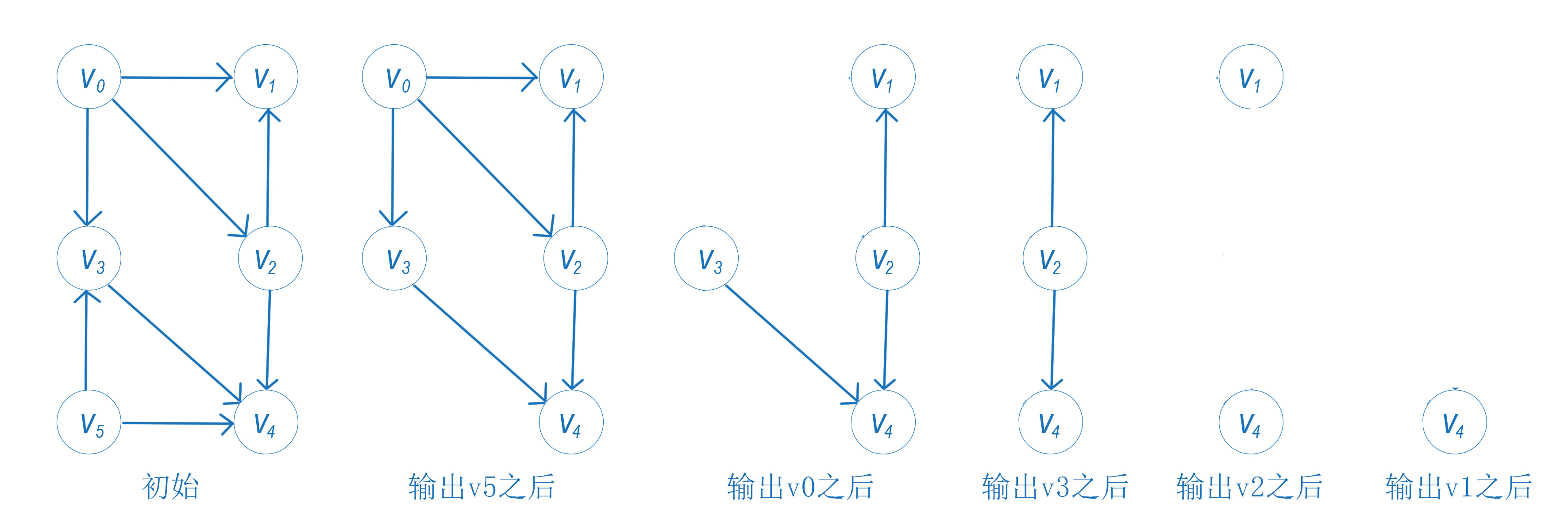
下图说明拓扑排序的过程。假设存在多个结点没有前驱，则任选一个顶点均可。

拓扑排序的实现：

首先求所有顶点的入度，然后在执行拓扑排序的过程中，当某个顶点的入度为零（即没有前驱顶点）时，就将此顶点输出，同时将该顶点的所有后继顶点的入度减1，以达到删除顶点和以它为尾的弧的操作。为了避免重复检测入度为零的顶点，使用栈存放入度为零的顶点。

const int MaxVertexNum = 20;
struct DNENode {
    int adjvex;
    int weight;
    struct DNENode * next;
};

template<typename T>
struct VNode {
    T data;
    DNENode * firstedge;
};

template <typename T>
class DNALGraph
{
public:
    DNALGraph();
    ~DNALGraph();
    int LocateVex(T u);                 //返回顶点u在图中的位置
    void FindInDegree(int indegree[]);  //求所有顶点的入度
    bool TopoSort();                    //拓扑排序
private:
    VNode<T> vertices[MaxVertexNum];    //顶点集
    int vexnum;                         //顶点数
    int arcnum;                         //边数
};

template<typename T>
void DNALGraph<T>::FindInDegree(int indegree[]) {
    int i;
    DNENode *p;
    for (i = 0; i < vexnum; ++i)
        indegree[i] = 0;
    for (i = 0; i < vexnum; ++i) {
        p = vertices[i].firstedge;
        while (p) {
            indegree[p->adjvex]++;
            p = p->next;
        }
    }
}

#include "stack"
template <typename T>
bool DNALGraph<T>::TopoSort() {
    int i, k, count = 0;
    int indegree[MaxVertexNum];     //入度数组，存放各顶点当前入度数
    int a[MaxVertexNum];
    stack<int> s(a, 0);
    DNENode *p;
    FindInDegree(indegree);         //对各顶点求入度
    for (i = 0; i < vexnum; ++i)    //将入度为0的顶点进栈
        if (!indegree[i])
            s.push(i);
    while (!s.empty()) {
        i = s.top();                //出栈并赋值
        s.pop();
        cout << vertices[i].data << ' ';    //输出i号顶点
        ++count;
        //对第i号顶点的每个邻接顶点进行处理
        for (p = vertices[i].firstedge; p; p = p->next) {
            k = p->adjvex;              //其序号为k
            if (!(--indegree[k]))       //k的入度减1，若减为0，则将其入栈
                s.push(k);
        }
    }
    if (count < vexnum) {       //零入度点栈已空时还有顶点没输出的情况
        cout << "There is a loop in the graph.\n";
        return false;
    } else {
        cout << " is a topological sort.\n";
        return true;
    }
}