【技巧】简单理解快速幂(求模)
今天讲了一个特别有用的东西就是快速幂,为了弄懂这个百度了一上午。。。还是没咋明白。。。
怕忘了就先开个博文记一下代码什么的。。。
快速幂,就是更快速地计算一个数的次方的方法。传统方法求幂计算,数小了还好,数大了就容易超时。
这个方法据说大部分比赛都不会超时,灰常地腻害呢~
具体理论总是太高大上了,还是举栗子好吃,简单又粗暴!
比如我们来算3的10次幂,把3乘10次脑袋就炸了,怎么算呢,这么算!
3*3*3*3*3*3*3*3*3*3…………………………(10个3相乘)①
=(3*3)*(3*3)*(3*3)*(3*3)*(3*3)…………………②
=(3*3)^5
=((3*3)*(3*3))^2*(3*3)………………………………………③
…啥?并没有感觉多好算?废话!人脑算起来当然难算,我们叫电脑来算啊~
先来看①式,如果要电脑来算,10个3相乘,就要乘9次;对于②式,五个3×3(把3×3看成一个整体)相乘,就要乘4次;对于③,就是两个((3*3)*(3*3))相乘再多乘一个多出来的(3*3),只要乘3次就好了,对于电脑来讲,工作的循环次数越少就越省时间(这个时候我还没学时间复杂度呢,我就先这样理解了╮(╯_╰)╭)。
这样就总结出来一个公式!
n^p (p为偶数时) n^p(p为奇数时)
=(n^2)^(p/2) =((n^2)^(p/2))*n
=((n^2)^2)^(p/2/2) =(((n^2)^2)^(p/2/2))*n
. .
. .
. .
=(n^p)*(1) =这个没固定公式(因为p每次除2之后奇偶性不固定)
(这个公式前提是不管p除多少个2商都是偶数)
而现实中情况更接近p为奇数的那种情况,,对于那种情况,变换也很简单,当p为奇数时,就把前面括号里的一堆东西(记为x)平方掉再乘以(p/2-0.5)(就是去尾法),注意还没完!还要再把去尾丢掉的一个x再乘上,就变成了 原式=(x^2)*(p/2-0.5)*x 当然程序里面如果p是整型变量就不用减去0.5了。
综合上面的东西,可以得出快速计算a的p次幂的函数代码:
long long QuickPow(long long a,long long p)
{
long long ans=1;
while(p)
{
if(p%2==1)//当p时奇数时,相当于往后面把那个少乘的x补乘上去
{
ans=ans*a;
}
p/=2;
a*=a;
}
return ans;
}有时候会叫你求a的p次幂除以mod(mod只是一个数)的余数,这时候就要用到同余定理了,同余定理式子是这样的:
(a*b)除以c的余数=(a除以c所得的余数)×(b除以c所得的余数),即(a*b)%c=(a%c)*(b%c),%是取余符号。
这样就会得到一个引理:
SO!
我们的代码就可以这样写了:
__int64 quickpow(__int64 a,__int64 p,__int64 mod)
{
__int64 ans=1;
a=a%mod;
while(p)
{
if(p%2==1)
{
ans=ans*a%mod;
}
p/=2;
a=a*a%mod;
}
return ans%mod;
}只是多往后面对mod取了个余罢了~
而我们上面的代码,就是当mod=1时的情况。
任务完成!
华丽分割-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=--=-=-=-=-=-=-=-=割分丽华
另附上学长给的代码:
//快速幂求模
#include<cstdio>
int quickpow(int n,int m,int mod)
{
int ans=1,base=n;
while(m)
{
if(m&1)
{
ans=(base*ans)%mod;
}
base=(base*base)%mod;
m>>=1;
printf("ans=%d base=%d m=%d\n",ans,base,m);
}
return ans;
}
int main()
{
int n,m,mod;
while(~scanf("%d%d%d",&n,&m,&mod))
{
printf("%d\n",mod);
printf("%d\n",quickpow(n,m,mod));
}
return 0;
}
唉,果然只有那些写出来让人看不懂的代码才能达到装逼的效果。。。→_→







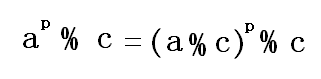














 1203
1203

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








