数据结构学习笔记（三）二叉树的非递归遍历

树的三种遍历方法很熟悉，常见的是用递归解决：

• 先序：根左右
• 中序：左根右

• 后序：左右根

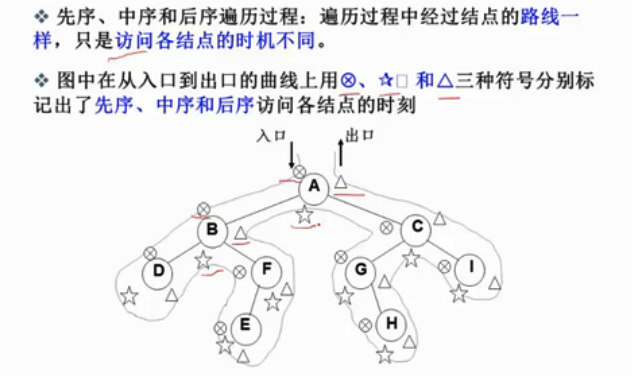
  仔细回想一下树的三种遍历算法，可以发现原来遍历过程中经过节点的路线一样，只是访问时机不同！

如上图，可以发现遍历过程中每个节点都有三次经过它的时机，如B点，首先经过它是先序遍历时，其次是中序遍历时，最后是后序遍历时那么。对于一个节点，第一次碰到就访问则是先序，第二次碰到访问是中序，第三次碰到访问是后序。我们可以根据此来讲递归程序转化为 非递归，借助堆栈来实现。

---

比如中序遍历，首先访问的是D节点，开始时我们的入口是A,但是我们不能访问它，而是要先访问它的左子树，当它的左子树访问完时，我们怎么知道要再回到A呢？那么久可以借助堆栈，先将根节点压入堆栈，当左子树都访问完时就要往回走，就将栈顶弹出。基本思路可如下：

• 碰到一个节点，压入堆栈，遍历其左子树，可用循环实现。
• 当其左子树遍历结束时，从栈顶弹出这个元素并访问它。

• 然后按其右指针在去便利该节点右子树。

  代码如下：

void PrevOrderTraversal(BiTree BT){
   BiTree T=BT;
   TreeNode temp;
   stack<TreeNode> S;
   InitStack(S);
   while(T||!S.empty()){
      while(T){
         S.push(T);
         T=T->left;
      }
      if(!S.empty()){
         temp=S.pop();
         printf("%d ",temp->data);
         T=T->right;
      }
   }
}

---

再来考虑前序遍历，就很简单了，因为前序遍历是第一次碰到的时候就访问，第一次碰到是在s.push() 的时候，所以只要将printf() 语句挪到上面去即可。

void InOrderTraversal(BiTree BT){
   BiTree T=BT;
   TreeNode temp;
   stack<TreeNode> S;
   InitStack(S);
   while(T||!S.empty()){
      while(T){
         printf("%d ",T->data);
         S.push(T);
         T=T->left;
      }
      if(!S.empty()){
         temp=S.pop();
         T=T->right;
      }
   }
}

---

那么后序遍历，又该怎样实现呢？
是否也可以借助堆栈实现后序遍历的非递归程序？是不是挪动一下printf语句就可以了？

后序遍历的非递归实现是三种遍历方式中最难的一种。因为在后序遍历中，要保证左孩子和右孩子都已被访问并且左孩子在右孩子前访问才能访问根结点，这就为流程的控制带来了难题。

后序遍历的顺序是左右根，那么我们碰到一个节点时先使其入栈，然后遍历其左子树，当其左子树遍历完时，该点出现在栈顶，此时我们能否将其弹出呢？是不能的哟，因为它的右子树还木有访问呢！此时弹出的话不久和中序遍历一样了？所以此时我们的方法是先不将栈顶元素弹出，而是遍历其右子树，当右子树遍历完时，该点第二次出现在栈顶，此时我们就可以将其弹出了！
那么怎么判断其是第一次碰到还是第二次碰到呢？可以设置一个变量标示其是第一次出现在栈顶。

代码如下：

void PostOrderTraversal(BinTree *root)    //非递归后序遍历
{
    stack<BTNode*> s;
    BinTree *p=root;
    BTNode *temp;
    while(p!=NULL||!s.empty())
    {
        while(p!=NULL)              //沿左子树一直往下搜索，直至出现没有左子树的结点 
        {
            BTNode *btn=(BTNode *)malloc(sizeof(BTNode));
            btn->btnode=p;
            btn->isFirst=true;
            s.push(btn);
            p=p->lchild;
        }
        if(!s.empty())
        {
            temp=s.top();
            s.pop();
            if(temp->isFirst==true)     //表示是第一次出现在栈顶 
             {
                temp->isFirst=false;
                s.push(temp);
                p=temp->btnode->rchild;    
            }
            else                        //第二次出现在栈顶 
             {
                cout<<temp->btnode->data<<" ";
                p=NULL;
            }
        }
    }    
} 

---

---

参考链接：
二叉树的非递归遍历