SVM(支持向量机)分类实用指导
Chih-Wei Hsu, Chih-Chung Chang, and Chih-Jen Lin
计算机科学系,国立台湾大学,台北 106,台湾
摘要
1 简介

 称为核函数。尽管不断有新的核函数被研究者提出,不过初学者应该可以在关于SVM的书籍
(推荐周志华所著清华大学出版社出版的《机器学习》)中找到以下四种基本的核函数:
称为核函数。尽管不断有新的核函数被研究者提出,不过初学者应该可以在关于SVM的书籍
(推荐周志华所著清华大学出版社出版的《机器学习》)中找到以下四种基本的核函数:
- 线性核:
- 多项式核:
- RBF(径向基)核(高斯核):
.
- Sigmoid核:
.
1.1 真实世界的例子
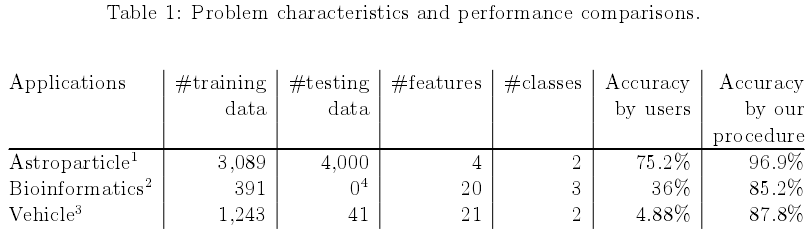
如表1所示是一些真实世界的例子,这些数据集由一些在一开始不能获得满意准确率的使用者提供,通过使用在本指导中阐述的处理流程后,我们帮助他们实现了更优秀的性能,具体的细节请查看附录A。
这些数据集可以在http://www.csie.ntu.edu.tw/~cjlin/papers/guide/data/下载。
1.2 建议处理流程
许多初学者通常使用以下处理流程:- 将数据转换成SVM包指定的格式
- 随机选择一些核和参数进行训练
- 测试
我们建议初学者先尝试以下处理流程:
- 将数据转换成SVM包指定的格式
- 对数据进行简单缩放处理
- 考虑使用RBF核
- 使用交叉验证找到最佳的参数
和
- 使用最佳参数
和
来训练整个数据集(最佳参数可能会受数据集大小的的影响,但是在实践中发现在交叉验证中获得的参数已经可以很好地拟合整个训练集)
- 测试
我们在接下来的章节中将详细阐述这些流程的细节。
2 数据预处理
2.1 名义型特征
SVM要求每个数据样本都能用实数向量来表示,因此,如果存在名义型属性,我们必须要先将它们转换成数字类型。我们推荐使用长度为m的元组来表示m-类的属性,其中只有一个数字为1,其余皆为0。例如一个3-类的属性比如{红、绿、蓝}可以替代为(0,0,1)、(0,1,0)、(1,0,0)。我们的经验告诉我们如果一个属性的元组长度越长,那么这种编码方法可能比使用单一的数字更加稳定。
2.2 数据缩放
在使用SVM训练模型前对数据进行缩放操作是十分有必要的,Sarle关于神经网络的FAQ(1997)的第二部分就对缩放和运用SVM时需要的考虑的地方的重要性进行了解释。缩放的主要好处就是防止各属性的值域差别过大,一些属性的值域的跨度大,而另外的跨度则较小。另一个好处就是可以避免数值计算困难,因为核函数的值通常取决于特征向量的内积,例如线性核核多项式核,大属性值可能会造成计算困难。我们建议通过线性缩放将每个属性缩放到[-1,+1]或[0,1]区间。
当然,我们需要对训练集和测试集使用同样的处理方法,例如,假设我们将训练数据的某个属性的值域从[-10,+10]缩放到[-1,+1],如果这个属性在测试集中的值域是在[-11,+8]之间,那么我们必须将测试数据缩放到[-1.1,+0.8]。附录B会给出一些实际的例子。
3 模型选择
尽管在第一节中只谈到了4种常用的核函数,但我们还是要先决定选择使用那个核,然后再选择惩罚系数和核参数。
3.1 RBF核
在选择核函数时通常RBF核是作为第一选择,这个核函数将样本非线性的映射到了一个更高维的空间,所以,不同于线性核,RBF核可以处理类标签和属性非线性相关的情况。此外,Keerthi and Lin (2003)提出线性核其实是RBF核的一种特殊情况,因为具有惩罚系数的线性核和具有参数(
,
)的RBF核有相同的性能。另外,sigmois核在特定的参数下也会表现得与RBF核类似(Lin and Lin, 2003)。
第二个原因就是超参数的个数会影响模型选择的复杂度,而多项式核具有比RBF核更多的超参数。
最后,RBF核具有更少的数值计算困难。关键的一点就是RBF核的值域固定在,相比之下多项式核的值在次数非常大的时候可能会取到无穷
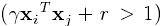
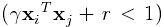
这里还有一些RBF核不合适使用的情况,特别是当特征的数量特别大时,这时可能更好使用线性核。我们将在附录C进行详细讨论。
3.2 交叉验证和梯度搜索
在RBF核和中主要有两个参数:和
,我们先前并不知道对于给定的问题
和
最佳的取值是多少,所以我们有必要进行模型选择(参数搜索)。我们的目标是找到一对足够好的(
,
)使得分类器可以准确的预测未知的数据(即测试集),请注意我们不必要去追求很高的训练准确率(即训练器可以准确预测那些标签已知的训练数据)。综上所述,一个常用的策略就是将数据集分成两部分,其中一个被认为是未知的(另一个被认为已知的用来训练模型),从这个“未知”的数据集中获得的预测精度可以准确的反应分类器在分类一个独立的数据集的性能,此过程的改进版本就被成为交叉验证。
对于v-折交叉验证,我们首先将训练集分割成v个大小相同的子数据集,接下来用其中v-1个子数据集训练的分类器来测试剩下的那个子数据集。因此,训练集中的每个样本都被预测过一次,交叉验证的精度就等于正确分类的样本所占训练集样本总数的百分比。
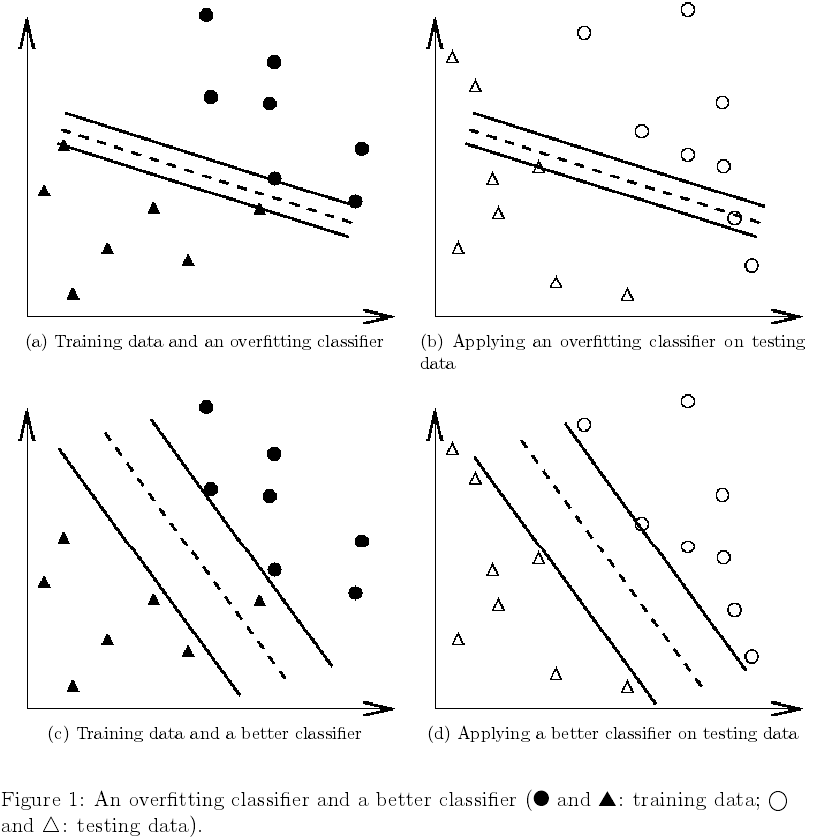
交叉验证还可以防止过拟合问题,如图1所示通过一个二分类问题来阐述这个问题,其中实心圆圈和三角形是训练数据,而空心圆和三角形是测试数据。在图1a和1b中由于过拟合,分类器测试的准确度并不理想,如果我们把在图1a和1b中的训练和测试数据看成是交叉验证中的训练集和验证集,结果还是不太好,另一方面,图1c和1d所示的分类器没有过拟合并且在获得更好的交叉验证结果的同时测试精度也提高了。
我们推荐利用交叉验证的方法通过梯度搜索来确定和
,通过对(
,
)不同的组合进行测试并选择其中具有最大交叉验证精度的组合,我们发现对
和
使用指数增长是一个实用的方法来找到满意的参数(例如,
)。
梯度搜索是一种简单直接但是似乎稍显天真的方法,事实上,这里还有一些更加先进,可以节省更多计算开销的方法,例如,估计交叉验证率。然而,这里有两个原因来说明我们为什么还是更喜欢这个简单的梯度搜索方法。
第一,从心理上,我们使用那些通过近似或启发式来避免进行全局搜索的方法可能会觉得不靠谱。另一个原因是通过梯度搜索来寻找满意参数所需的计算时间并不会比那些先进的方法更多,因为这里只有两个参数需要确定。另外,梯度搜索可以很容易实现并行化,因为每次交叉验证都是独立的,而很多先进的算法,比如,walking along a path是一个迭代的过程,很难实现并行化。
不过完成一个完整梯度搜索仍然是十分耗时的,我们建议在开始的时候使用粗略的梯度,在找到一个最佳的梯度区间后,再在该区间进行精细的梯度搜索。为了说明这个过程,我们通过german问题来做一个实验,在进行缩放后,我们一开始使用一个粗略的梯度(如图2所示)找到最佳的(,
)取值是
——拥有77.5%的交叉验证精度。接下来我们在
附近进行精细的提度搜索(如图3所示)并且在
获得了最佳的交叉验证精度77.6%。再找到了最佳的(
,
)对后,重新训练整个训练集得到最终的分类器模型。
以上的方法在上千或者更多的数据大小时工作效果良好,而对于超大型数据集来说,一个可行的方法是随机选择数据集的一个子集,在该子集上进行粗略的梯度搜索,再在整个数据集上进行精细的梯度搜索。
4 讨论
以上提到的方法可能在一些情况下表现不会足够好,所以其他一些技术,例如,特征选择还是需要的,不够这些内容已经超越本指导的范畴了。我们的实验证实了这些处理方法对于那些没有很多特征的数据效果显著。当需要处理成千上万的属性时,在将数据传递给SVM之前或许需要先对它们进行挑选。
致谢
我们感谢所有使用我们的软件LIBSVM和BSVM,帮助我们认清初学者可能遇到的困难的用户,还有那些对本文进行校对的用户(特别是Robert Campbell)。










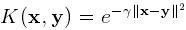


















 1838
1838

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








