汤普森采样（Thompson sampling）

1、Beta分布

• 定义域：[0,1]
• 参数：$\alpha ,\beta$，均为正值参数，又称为形状参数

1.1 Beta分布的概率密度函数

$$\begin{gathered} f(x,\alpha ,\beta )=constant\cdot x^{\alpha -1}\cdot (1-x{)}^{\beta -1} \\ =\frac{x^{\alpha -1}(1-x{)}^{\beta -1}}{{\int }_0^1{u}^{\alpha -1}(1-u{)}^{\beta -1}\mathrm{d}u} \\ =\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}{x}^{\alpha -1}(1-x{)}^{\beta -1} \\ =\frac{1}{B(\alpha ,\beta )}{x}^{\alpha -1}(1-x{)}^{\beta -1} \end{gathered}$$

\quad 其中，$\Gamma$ 为 Gamma 函数，是阶乘的扩展：

• 当n为正整数时，n的阶乘定义如下：$n!=n\ast (n-1)\ast (n-2)\ast \dots \ast 2\ast 1$
• 当n不是整数时，n!为：
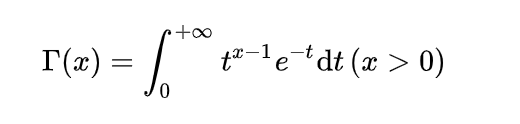
  Beta分布的均值是：
  $$\frac{\alpha }{\alpha +\beta }$$
  Beta分布的方差是：
  $$\frac{\alpha \beta }{(\alpha +\beta {)}^2(\alpha +\beta +1)}$$
  Beta分布的图形：
  
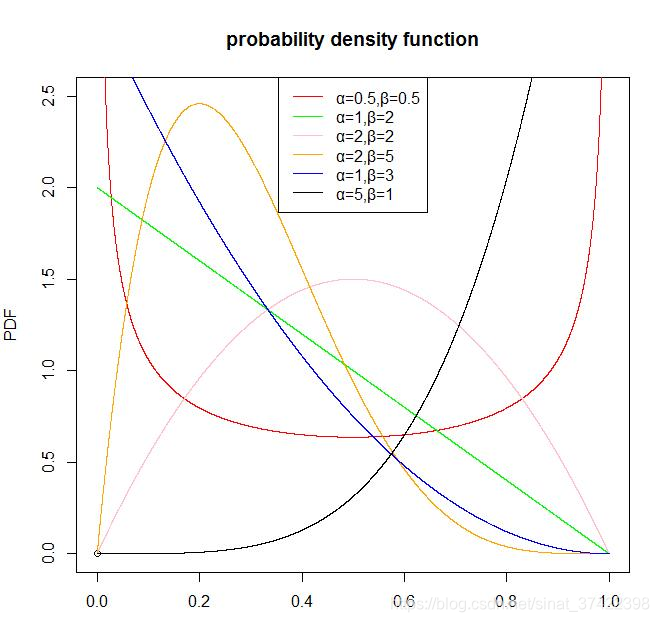
  \quad 从Beta分布的概率密度函数的图形我们可以看出，Beta分布有很多种形状，但都是在0-1区间内，因此Beta分布可以描述各种0-1区间内的形状（事件）。因此，它特别适合为某件事发生或者成功的概率建模。同时，当α=1，β=1的时候，它就是一个均匀分布。
  \quad 贝塔分布主要有 α和 β两个参数，这两个参数决定了分布的形状，从上图及其均值和方差的公式可以看出：
  1）α/(α+β)也就是均值，其越大，概率密度分布的中心位置越靠近1，依据此概率分布产生的随机数也多说都靠近1，反之则都靠近0。
  2）α+β越大，则分布越窄，也就是集中度越高，这样产生的随机数更接近中心位置，从方差公式上也能看出来。

1.2 棒球运动员击球率的例子

\quad 为了衡量一个棒球运动员的击球率。
\quad 首先在运动员打球之前，我们就先对他的击球率有一个预测值（先验概率）。假设我们预计运动员整个赛季的击球率平均值大概是0.27左右，范围大概是在0.21到0.35之间（根据历史运动员的击球率）。那么用贝塔分布来表示，我们可以取参数 α=81，β=219，因为α/(α+β)=0.27，图形分布也主要集中在0.21~0.35之间，非常符合经验值，也就是我们在不知道这个运动员真正击球水平的情况下，我们先给一个平均的击球率的分布。

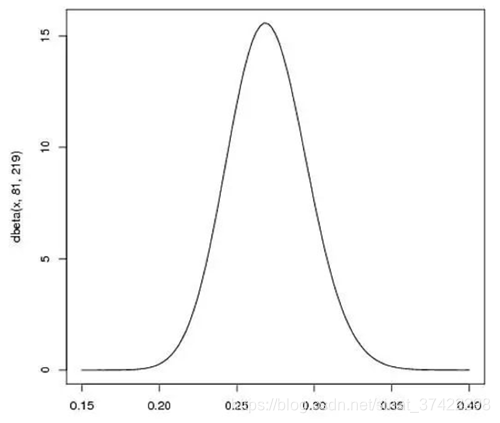
\quad 假设运动员一次击中，那么现在他本赛季的记录是“1次打中；1次打击”。那么我们更新我们的概率分布，让概率曲线做一些移动来反应我们的新信息。
$$Beta({\alpha }_0+hits,{\beta }_0+misses)$$
\quad 其中，${\alpha }_0=81、{\beta }_0=219$是初始参数。hits表示击中的次数，misses表示未击中的次数。假设赛季过半时，运动员一共打了300次，其中击中100次。那么新的贝塔分布是Beta(81+100,219+200)，如下图：

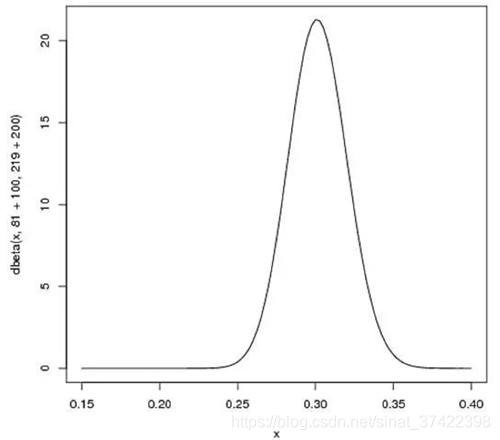
\quad 可以看出，曲线更窄而且往右移动了（击球率更高），由此我们对于运动员的击球率有了更好的了解。新的贝塔分布的期望值为0.303，比直接计算100/(100+200)=0.333要低，是比赛季开始时的预计0.27要高，所以贝塔分布能够抛出掉一些偶然因素，比直接计算击球率更能客观反映球员的击球水平。

总结：

\quad 这个公式就相当于给运动员的击中次数添加了“初始值”，相当于在赛季开始前，运动员已经有81次击中219次不中的记录。 因此，在我们事先不知道概率是什么但又有一些合理的猜测时，贝塔分布能够很好地表示为一个概率的分布。

参考：
推荐算法之Thompson(汤普森)采样 - 光彩照人 - 博客园
贝塔分布（Beta Distribution）简介及其应用 | 数据学习者官方网站(Datalearner)

2、Multi-Armed Bandit

2.1 简介

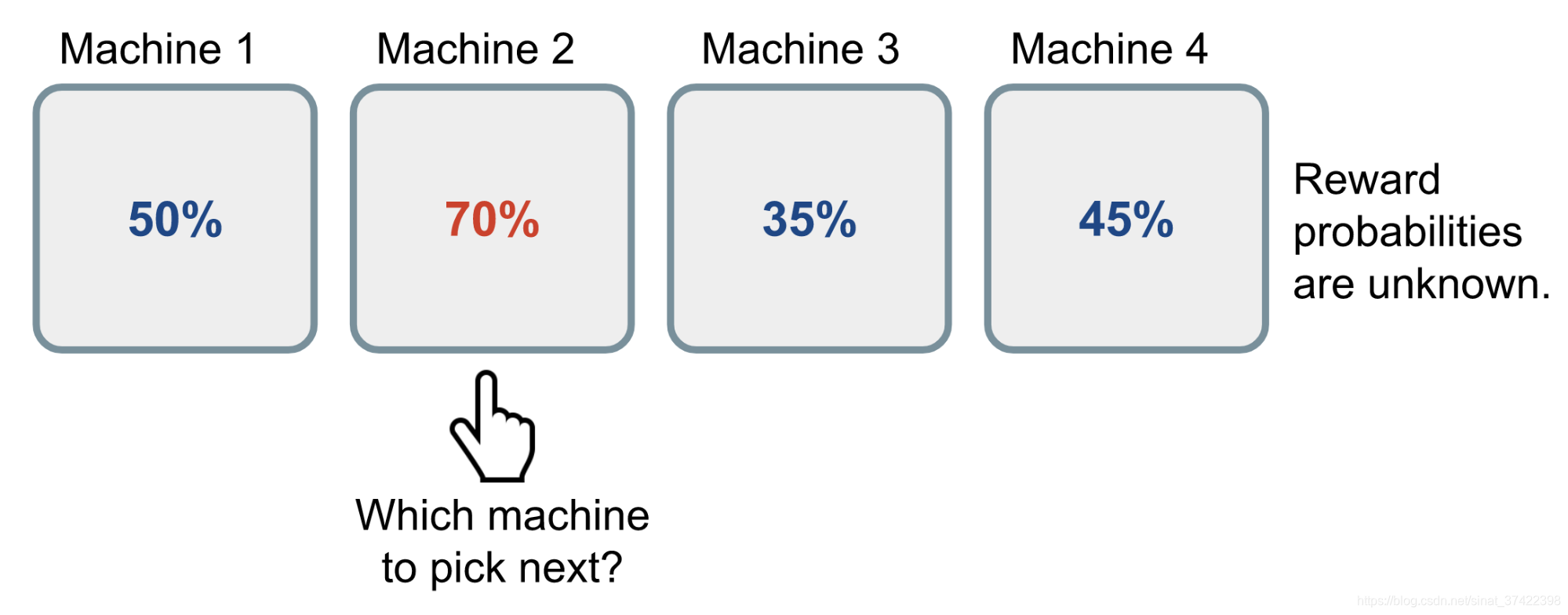
\quad 我们有 k 个Bandit，每个Bandit都有获得收益的概率，但是未知，所以我们只能通过实验来计算这个概率。根据大数定律，随着我们在一个 Bandit 上试验次数越来越多，频率=概率，我们就可以得到该 Bandit 收益率 的“真实值”。
\quad 但是每次实验需要投1币，在每一个Bandit上做大量试验代价太大。
\quad 所以我们需要在 向当前已知的收益率最大的Bandit投币（利用） 和 向没怎么探索的Bandit投币（探索） 两个选择之间进行权衡。

2.2 问题定义

\quad Bernoulli multi-armed bandit 问题可以用一个 二元组 $<\mathcal{A},\mathcal{R}>$来描述：

• 我们有 $K$ 个Bandits，获得收益的概率为 { θ 1 , . . . , θ K } \{\theta_1,...,\theta_K\} {θ1​,...,θK​}
• 在每一个时间步 $t$，我们都会在一台 Bandit 上采取一个 action $a$，并且获得 reward $r$
• $\mathcal{A}$ 是动作集合，每一个动作表示与一台Bandit进行交互。动作 $a$ 的价值是 expected reward $Q(a)=\mathbb{E}[r|a]=\theta$。如果在时间步 $t$ 做出的 action $a_t$ 是与 Bandit $i$ 进行交互，那么 $Q(a_t)={\theta }_i$
• $\mathcal{R}$ 是 reward function。在 Bernoulli bandit 例子中，我们得到的 reward 是具有随机性的。在一个时间步 $t$，$r_t=\mathcal{R}(a_t)$ 会以 $Q(a_t)$ 的概率为1，其他情况下为0。

2.3 Bandit Strategies

\quad 基于如何进行探索，有多种方式解决 the multi-armed bandit：

• No exploration：最差的方式，例如：$GreedyAlgorithm$
• Exploration at random：$ϵ-GreedyAlgorithm$
• Exploration smartly with preference to uncertainty：UCB、Thompson Sampling
  

3 ε-Greedy Algorithm

4 Upper Confidence Bounds

\quad 完全随机的探索 可能会选择到已经被证实了的收益率低的 Bandit，所以这种方法是低效的。有两种方法解决：1）降低 $ϵ$ 的值；2）探索具有高价值 潜力 的action（直观上理解就是没咋探索过的，而且根据历史经验收益率不是很低的）。
\quad 如何衡量这种 高价值潜力？
\quad The Upper Confidence Bounds (UCB) algorithm 计算了 reward value 的置信上界 ${\hat{U}}_t(a)$:

4.1 Hoeffding’s Inequality

4.2 UCB1

\quad 自适应的 $p$。设置 $p=t^{-4}$ ：

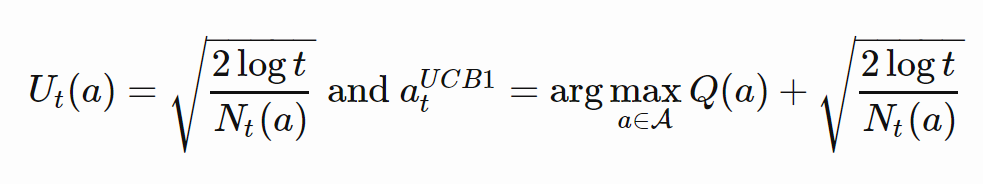
4.3 Bayesian UCB

\quad 在 UCB 和 UCB1 算法中，我们没有对奖励的先验分布进行假设，所以根据 Hoeffding 不等式得到的各个 Bandit 的 reward 的分布 是很相似的。
\quad 如果我们能提前知道 先验分布 ，就能更好地估计 reward 的 上界。

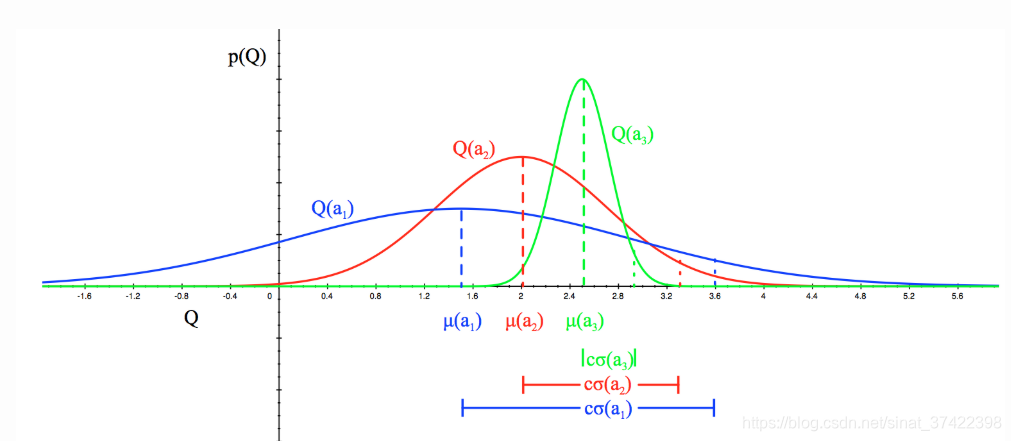
\quad 我们希望每个 Bandit 的 平均reward $Q(a)$ 都服从下图的高斯分布 $p(Q)$，我们希望 $Q(a)<={\hat{Q}}_t(a)+U_t(a)$ 以 95% 的概率成立（即，置信率95%），所以置信区间需要为 $[\mu -2\delta ,\mu +2\delta ]$。所以需要 ${\hat{Q}}_t(a)+U_t(a)=\mu +2\delta$，即 $U_t(a)=2\delta$为2倍的标准差，其中$\mu ={\hat{Q}}_t(a)$为样本均值。

5、Thompson Sampling

举个视觉上很直观的例子：

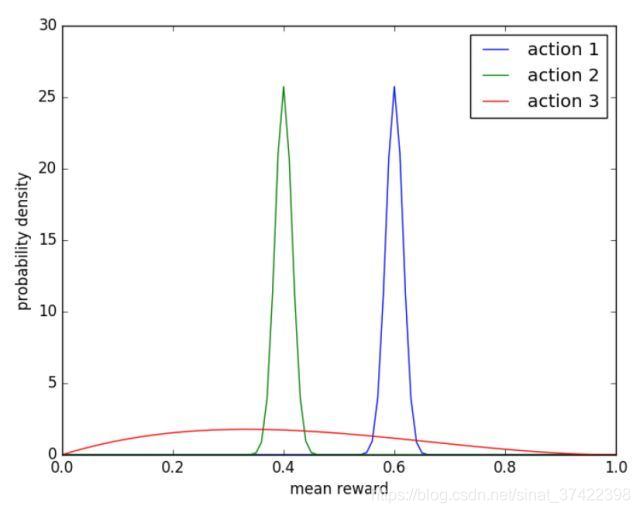
\quad 上图 action 1，2，3的分布就分别为Beta(601,401),Beta(401,601),Beta(2,3). 所以，这里我们也能定量化地看出action 3之前试验的次数比较少，而action 1,2之前试验的次数已经很多了。


\quad 在Beta Bernoulli Bandit情形下的，贪心算法，和TS算法的伪代码如上图所示。
\quad 主要的区别在于两个算法中贪心算法每个time step第一步是estimate model，而TS算法中第一步则是sample model。也就是说，${\hat{\theta }}_k$决定的方法不同，一个是直接用sample average，即从sample中估计出来的成功率，因此根据历史经验收益率大的Bandit相应的${\hat{\theta }}_k$大，就会被选中。而与此不同的就是TS算法是sample一个model，即${\hat{\theta }}_k$是直接从后验的$Beta({\alpha }_k,{\beta }_k)$分布中采样出来，对于没咋被探索的Bandit，例如 action 3 ，它的 ${\hat{\theta }}_{action3}$是从红色曲线分布中采样出来的，相当于一个均匀分布，所以 ${\hat{\theta }}_{action3}$ 仍有可能比较大，所以被探索的概率也比较高。