1.4 关于排序的讨论
- 排序算法在计算机算法中占有重要位置
- 根据时间复杂度,排序算法可分为两类:
- 复杂度为 O ( n 2 ) \bm{O(n^2)} O(n2):大多较直观
- 复杂度为
O
(
n
l
o
g
n
)
\bm{O(nlogn)}
O(nlogn):执行效率高
- 要理解排序算法,就要先掌握 递归和分治
1.4.1 直观的排序算法时间到底浪费在哪里?
假设序列有 N 个元素,存于一个数组 a [ N ] a[N] a[N] 中,如何对它做从小到大排序?
- 选择排序(Selection Sort):
- 每轮从序列中选出一个最大值放在最后,直到排序完毕
- 步骤1:从头到尾 (
N) 比较相邻两个元素,小的放前面,大的放后面。第一轮扫描进行N-1次比较和少于N-1次交换,得到最末的最大元素 - 步骤2:从头到倒数第二个元素 (
N-1) ,重复步骤1,每轮比之前少一个元素,以此类推 - 时间复杂度为
O
(
n
2
)
\bm{O(n^2)}
O(n2)
(N-1)+(N-2)+ … +1 - 动图演示(每轮选一个最小值放最前):

// 选择排序
public static void selectionSort(Comparable[] data)
{
int min;
for(int index = 0 ; index < data.length - 1; index++) // 控制存储位置
{
min = index;
for(int scan = index + 1; scan < data.length; scan++) // 查找余下数据
if (data[scan].compareTo(data[min]) < 0) // 查找最小值
min = scan;
swap(data,min,index); // 交换赋值
}
}
private static void swap(Comparable[] data,int index1,int index2){
Comparable temp = data[index1]; // 引入一个临时变量
data[index1] = data[index2];
data[index2] = temp;
}
- 选择排序 “太笨”,复杂度直接达到排序算法的上界
- 插入排序(Insert Sort):
- 类似打扑克 “一边抓牌 一边插牌” 的过程
- 步骤1:取最后一个元素 a [ N ] a[N] a[N],和第一个元素 a [ 1 ] a[1] a[1] 比较,插入并成为数组中第二个元素(需要给新元素 “留空位”),复杂度为 O ( N ) O(N) O(N)
- 步骤2:取第二个元素 a [ N − 1 ] a[N-1] a[N−1],依次和排好序的元素比较,找到位置后,先平移元素腾出位置再插入,以此类推,每轮排好一个数
- 时间复杂度依然是: O ( n 2 ) \bm{O(n^2)} O(n2)
- 优化:可用二分查找找到插入位置( l o g n logn logn 次)
- 动图演示(从后向前扫描比较):

// 插入排序
public static void insertionSort (Comparable[] data)
{
for (int index = 1; index < data.length; index++)
{
Comparable key = data[index];
int position = index;
// 哨兵临时存储
while (position > 0 && data[position-1].compareTo(key) > 0)
{
data[position] = data[position-1]; //位置全部后移
position--;
}
data[position] = key; //合适位置
}
}
- 以上两种排序算法虽然直观,但无用功多,比如选择排序:
- 对所有元素都进行了两两比较
- 做了很多无用的元素位置互换
1.4.2 有效的排序算法效率来自哪里?
将序列 a[1…N] 划分成 B、C 两个子序列,每个子序列有 N / 2 N/2 N/2 个元素,假设它们已排好序,即 b [ 1 ] b[1] b[1]、 b [ 2 ] b[2] b[2]、 b [ N / 2 ] b[N/2] b[N/2] 和 c [ 1 ] c[1] c[1]、 c [ 2 ] c[2] c[2]、 c [ N / 2 ] c[N/2] c[N/2] 均有序,如何对 B、C 排序?
- 归并排序(Merge Sort):
- 由冯·诺依曼发明,分治和递归的典型应用
- 步骤1:比较 b [ 1 ] b[1] b[1] 和 c [ 1 ] c[1] c[1],确定最小元素,赋给 a [ 1 ] a[1] a[1](合并)
- 步骤2:假设 a [ 1 ] = b [ 1 ] a[1]=b[1] a[1]=b[1],则 a [ 2 ] = m i n ( b [ 2 ] , c [ 1 ] ) a[2]=min(b[2],c[1]) a[2]=min(b[2],c[1]),以此类推
- 步骤3:一个子序列被合并完后,另一个子序列的剩余部分直接加入序列
- B、C 子序列如何排序?重复上述过程,假定它们的前一半和后一半也分别排好了序,直到子序列中只剩一个元素(递归)
-
规律:第 K = logN 次排序,有 N 个子序列,每个长度是原始序列(n)的 1/N,每次排序的复杂度都是 O ( n ) \bm{O(n)} O(n)(最多进行 n 次比较; O ( n / N ∗ N ) O(n/N*N) O(n/N∗N))
- 时间复杂度为 O ( n l o g n ) \bm{O(nlogn)} O(nlogn),空间复杂度为 O ( n ) \bm{O(n)} O(n)
- 动图演示(子序列递归合并为序列):

// 归并排序(伪代码)
public static void mergeSort (Comparable[] data, int min, int max)
{
if (min < max)
{
int mid = (min + max) / 2;
mergeSort (data, min, mid);
mergeSort (data, mid+1, max);
merge (data, min, mid, max);
}
}
- 归并排序虽然在时间复杂度上少做了无用功,但其空间复杂度不算太经济(需要两组存储空间来回替换使用)
- 后来,加拿大计算机科学家约翰·威廉斯提出 堆排序算法,拥有归并排序的时间复杂度,又不占用额外空间(就地特征; O ( 1 ) O(1) O(1))
- 接着,英国计算机科学家托尼·霍尔对相同数量级的算法做出改进,发明了比归并排序和堆排序快 2-3 倍的 快速排序算法,且空间复杂度为 O ( l o g n ) O(logn) O(logn)
- 堆排序(Heap Sort):
- 基本思想:利用堆的特性(近似完全二叉树的结构)所设计,其子节点的值总是小于(或者大于)它的父结点,以此递归地建立小顶堆或大顶堆,逐个存储有序元素
- 动图演示(建立大顶堆):

// 堆排序
public static void heapSort(int[] arr){
for (int i = arr.length/2-1; i >= 0 ; i--) {
adjustHeap(arr,i,arr.length);
}
for (int j = arr.length-1; j > 0; j--) {
int temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
adjustHeap(arr,0,j);
}
}
/**
* 构建大顶堆:将以i对应的非叶子结点的子树调整成大顶堆
*/
public static void adjustHeap (int[] arr,int i,int length){
/*取出当前非叶子结点的值保到临时变量中*/
int temp = arr[i];
/*j=i*2+1表示的是i结点的左子结点*/
for (int j = i * 2 + 1; j < length ; j = j * 2 + 1) {
if (j+1 < length && arr[j] < arr[j+1]){ //左子结点小于右子结点
j++; //j指向右子结点
}
if (arr[j] > temp){ //子节点大于父节点
arr[i] = arr[j]; //把较大的值赋值给父节点
//arr[j] = temp; 这里没必要换
i = j; //让i指向与其换位的子结点 因为
}else{
/*子树已经是大顶堆了*/
break;
}
}
arr[i] = temp;
}
}
- 快速排序(Quick Sort):
- 基本思想:先选择一个数作为基准,根据基准移动交换元素,对序列分区(如小的在基准前,大的在基准后),再递归地在左右子区间选择基准进行分区,直到各区间只剩一个数
- 动图演示(选择第一个数作为 pivot):

// 快速排序
public static void quickSort (Comparable[] data, int min, int max)
{
int pivot;
if (min < max)
{
pivot = partition (data, min, max); // 选择基准
quickSort(data, min, pivot-1); // 左分区排序
quickSort(data, pivot+1, max); // 右分区排序
}
}
private static int partition (Comparable[] data, int min, int max)
{
Comparable partitionValue = data[min];
int left = min;
int right = max;
while (left < right)
{
while (data[left].compareTo(partitionValue) <= 0 && left < right)
left++;
while (data[right].compareTo(partitionValue) > 0)
right--;
if (left < right)
swap(data, left, right);
}
swap (data, min, right);
return right;
}
- 但就 “稳定性 ”而言,归并排序比其他两种算法更胜一筹
- 稳定:如果 a 原本在 b 前面,而 a=b,排序之后 a 仍然在 b 前面
- 不稳定:如果 a 原本在 b 前面,而 a=b,排序之后 a 可能会出现在 b 后面
- 另外,在极端情况下,快速排序的时间复杂度并不高效
- 三种排序算法对比如下:
| 算法 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|
| 归并排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n ) O(n) O(n) | √ |
| 堆排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( 1 ) O(1) O(1) | × |
| 快速排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n 2 ) O(n^2) O(n2) | O ( l o g n ) O(logn) O(logn) | × |
【思考题 1.4.1】
【问】假定有 25 名短跑选手比赛争夺前三名,赛场上有五条赛道,一次可以有五名选手同时比赛。比赛并不计时,只看相应的名次。假设选手的发挥是稳定的,也就是说如果约翰比张三跑得快,张三比凯利跑得快,约翰一定比凯利跑得快。最少需要几次比赛才能决出前三名?
【答】在每位选手每次比赛都发挥稳定、不出意外、可分辨名次的情况下,最少需要 7 次比赛,步骤如下:
- 将 25 位选手分成 5 组(A、B、C、D、E)
- 组内选手先进行比赛,共 5 次,5 组选手组内排名如下(“>”表示速度):
- A 1 > A 2 > A 3 > A 4 > A 5 A1 > A2 > A3 > A4 > A5 A1>A2>A3>A4>A5
- B 1 > B 2 > B 3 > B 4 > B 5 B1 > B2 > B3 > B4 > B5 B1>B2>B3>B4>B5
- C 1 > C 2 > C 3 > C 4 > C 5 C1 > C2 > C3 > C4 > C5 C1>C2>C3>C4>C5
- D 1 > D 2 > D 3 > D 4 > D 5 D1 > D2 > D3 > D4 > D5 D1>D2>D3>D4>D5
- E 1 > E 2 > E 3 > E 4 > E 5 E1 > E2 > E3 > E4 > E5 E1>E2>E3>E4>E5
- 每组第一名进行比赛,共 1 次,假设比赛结果为(“>”表示速度):
- A 1 > B 1 > C 1 > D 1 > E 1 A1 > B1 > C1 > D1 > E1 A1>B1>C1>D1>E1
- 由此可决出第 1 名
- 在剩下的选手中,一共 5 人出线:
- D、E 组可直接淘汰(D1 已拿不到前3)
- C 组 C1 出线
- B 组 B1、B2 出线
- A 组 A2、A3 出线
- 这 5 人再进行 1 次 比赛,即可决出第 2、3 名(对应这次比赛第 1、2 名)
综上,要决出前三名,最少要进行 5+1+1=7 次比赛。
【思考题 1.4.2】
【问】如果有 N 个区间 [ l 1 , r 1 ] , [ l 2 , r 2 ] , . . . , [ l N , r N ] [l_{1},r_{1}], [l_{2},r_{2}], ..., [l_{N},r_{N}] [l1,r1],[l2,r2],...,[lN,rN],只要满足下面的条件我们就说这些区间是有序的: ∃ x i ∈ [ l i , r i ] ∃\,x_{i}∈[l_{i},r_{i}] ∃xi∈[li,ri],其中 i = 1 , 2 , . . . , N i=1,2,...,N i=1,2,...,N
比如,[1, 4]、[2, 3] 和 [1.5, 2.5] 是有序的,因为我们可以从这三个区间中选择 1.1、2.1 和 2.2 三个数。同时 [2, 3]、[1, 4] 和 [1.5, 2.5] 也是有序的,因为我们可以选择 2.1、2.2 和 2.4。但是 [1, 2]、[2.7, 3.5] 和 [1.5, 2.5] 不是有序的。
对于任意一组区间,如何将它们进行排序?
【答】由题意可知,对于任意三个区间,如果它们有共同的交集,可互换顺序,且一直保持有序状态,因为每个区间里的浮点数是无限的,对于 N 个区间,只要有交集,总是可以从它们的交集中选择 N 个有序排列的点,例如:[1, 4]、[2, 3] 和 [1.5, 2.5] 的交集是 [2, 2.5](如下图),因此不论怎么排列有交集的三个区间,都可以从三个区间任意找出 3 个有序的点,即这三个区间有序。
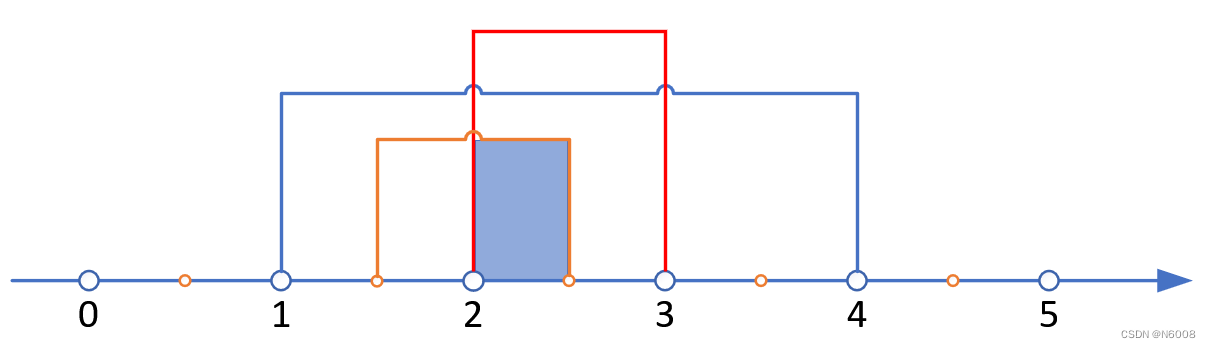
按照上面的思路,每个区间都可以简化成一个随机点。对于 [1, 2]、[2.7, 3.5] 和 [1.5, 2.5],这三个区间并没有交集,但 [1, 2] 和 [1.5, 2.5] 存在交集 [1.5, 2],我们可以观察它们并集(端点)和无交集区间 [2.7, 3.5] 的位置决定顺序(如下图),我们发现:[2.7, 3.5] 在并集右端点的右侧,因此在排序时,将 [2.7, 3.5] 放在最后即可,有交集的两个区间则不需要排序。
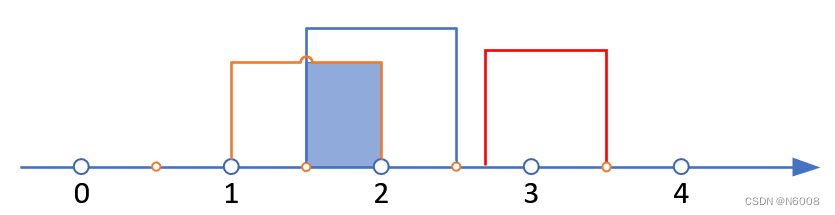
对于三个区间,除以上两种情形外,还有一种情况(三个区间相互没有交集,但区间1和区间2、区间2和区间3有交集,如下图):
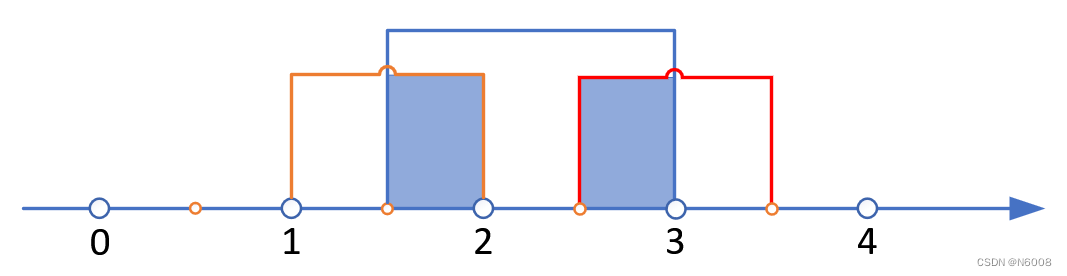
这时,如果需要排序,就需要固定三个区间的顺序了,对它们的左端点或右端点统一排序,三个点的顺序即为区间的顺序。
- 总结一下给三个区间排序的情况:
- 三个区间有交集,则三个区间自然有序(不需要排序);
- 三个区间没有交集,但其中两个区间有 1 个交集,则需要考虑有交集区间的并集之间的相对位置,即给 “没有交集区间” 和 “有交集区间的并集” 的端点排序;
- 三个区间没有交集,但其中两个区间有 2 个交集,则需要给三个区间的左端点或右端点统一排序,端点顺序即可代表区间顺序。
- 再将三个区间延伸到 N 个区间的情况,可得:
- N 个区间有交集,则这 N 个区间自然有序;
- N 个区间没有交集,但其中至少存在两个区间有 1 个交集(共有 1 ~ N-2 个交集),则需要给 “没有交集区间” 和 “有交集区间的并集” 的左端点或右端点统一排序,端点顺序即可表示区间顺序,存在交集的区间自然有序;
- N 个区间没有交集,但其中两两区间之间均有交集(共有 N-1 个交集),则需要给这 N 个区间的左端点或右端点统一排序,端点顺序即可表示区间顺序
这里,判断 N 个区间的交集个数,可能需要穷举法,确定对应情况后,给端点排序则可以使用归并排序等算法。
总结
- 通过阅读学习前两小节 5 种直观和高效的排序算法,我们基本认识了分治和递归思想及其在排序算法中的重要性,也总结出在计算机领域做事的两个原则:
- 尽可能避免做大量无用功(选择排序、插入排序)
- 在多个考量维度下,接近最优的算法可能有很多种
参考资料
- 《计算之魂》第一章
- 十大经典排序算法(动图)
- 堆排序实现






















 1205
1205











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








