Java&C++题解与拓展——leetcode587.安装栅栏【二维凸包学习】

每日一题做题记录，参考官方和三叶的题解

题目要求

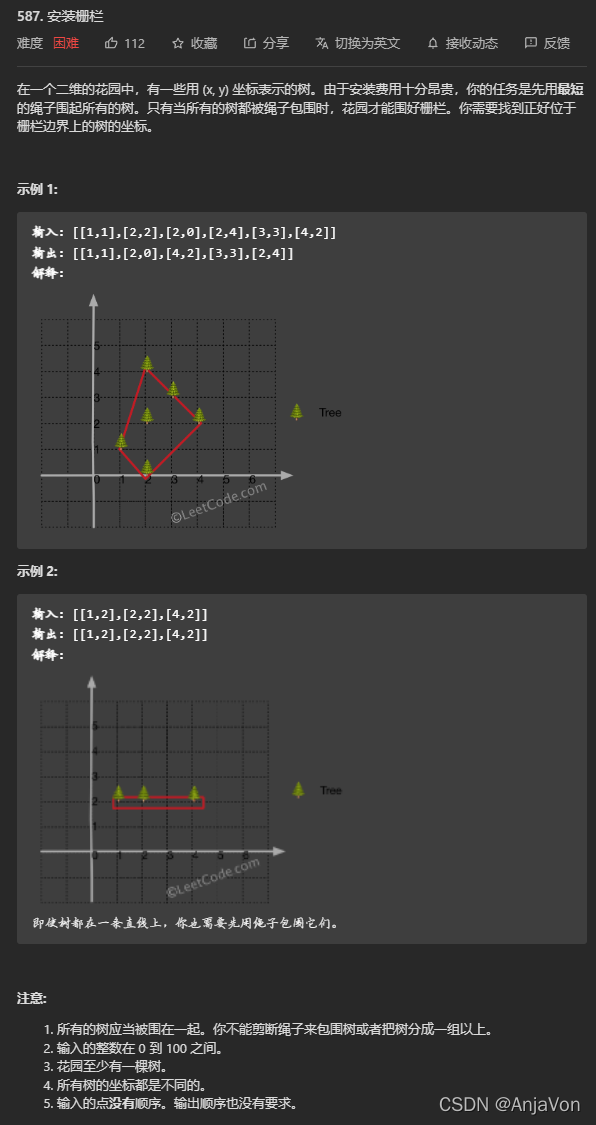
求凸包

明显是一道求凸包的题，虽然在今天之前完全不知道这是个啥……

所以就去wiki了一下，然后做了一点小笔记小理解，可以看这里👉凸包学习，后面就直接写实现思路，不在算法原理多着笔墨。

思路一：Jarvis算法

从最左的点开始，那么要解决的问题就在于找当前最靠左的向量。

使用向量叉乘cross判别，$\overrightarrow{ab}\times \overrightarrow{bc}$：

• 结果大于零，夹角小于180°，则从$\overrightarrow{ab}$到$\overrightarrow{bc}$为逆时针旋转，此时点$c$一定在向量$\overrightarrow{ab}$左边；
• 结果等于零，夹角等于180°，两向量平行，三点共线；
• 结果小于零，夹角大于180°，则从$\overrightarrow{ab}$到$\overrightarrow{bc}$为顺时针旋转，此时点$c$一定在向量$\overrightarrow{ab}$右边。

通过遍历所有点，找到对于点$a$来说逆时针最靠外的点$b$，其余所有点都在向量$\overrightarrow{ab}$左边。

若存在两个点相对于$a$在同一条线上，应当将$a$和$b$同一线段上的边界点都考虑进来，此时需进行标记防止重复添加。

Java

class Solution {
    public int cross(int[] a, int[] b, int[] c) { // 叉乘
        return (b[0] - a[0]) * (c[1] - b[1]) - (b[1] - a[1]) * (c[0] - b[0]);
    }
    public int[][] outerTrees(int[][] trees) {
        int n = trees.length;
        if(n < 4)
            return trees;

        int left = 0; // 找到最左下的一点，作为起始点
        for(int i = 0; i < n; i++)
            if(trees[i][0] < trees[left][0] || (trees[i][0] == trees[left][0] && trees[i][1] < trees[left][1]))
                left = i;

        List<int[]> res = new ArrayList<int[]>();
        boolean[] vis = new boolean[n];
        int a = left;
        do{
            int b = (a + 1) % n; // 下一个凸包点
            for(int c = 0; c < n; c++)
                if(cross(trees[a], trees[b], trees[c]) < 0) // ab到ac为顺时针，即c在ab的右边
                    b = c;
            
            for(int c = 0; c < n; c++) {
                if(vis[c] || c == a || c == b)
                    continue;
                if(cross(trees[a], trees[b], trees[c]) == 0) { // 共线
                    res.add(trees[c]);
                    vis[c] = true;
                }
            }
            if(!vis[b]) {
                res.add(trees[b]);
                vis[b] = true;
            }
            a = b; // 以b为起始
        } while(a != left); // 转回起始点停下
        return res.toArray(new int[][]{});
    }
}

• 时间复杂度：$O(n^2)$，判断每个点时都要遍历所有点，即判断$n$次过程中遍历$n$次。
• 空间复杂度：$O(n)$，标记每个点。

C++

class Solution {
public:
    int cross(vector<int> &a, vector<int> &b, vector<int> &c) { // 叉乘
        return (b[0] - a[0]) * (c[1] - b[1]) - (b[1] - a[1]) * (c[0] - b[0]);
    }
    vector<vector<int>> outerTrees(vector<vector<int>>& trees) {
        int n = trees.size();
        if(n < 4)
            return trees;

        int left = 0; // 找到最左下的一点，作为起始点
        for(int i = 0; i < n; i++)
            if(trees[i][0] < trees[left][0] || (trees[i][0] == trees[left][0] && trees[i][0] < trees[left][0]))
                left = i;

        vector<vector<int>> res;
        vector<bool> vis(n, false);
        int a = left;
        do{
            int b = (a + 1) % n; // 下一个凸包点
            for(int c = 0; c < n; c++)
                if(cross(trees[a], trees[b], trees[c]) < 0) // ab到ac为顺时针，即c在ab的右侧
                    b = c;

            for(int c = 0; c < n; c++) {
                if(vis[c] || c == a || c == b)
                    continue;
                if(cross(trees[a], trees[b], trees[c]) == 0) { // 共线
                    res.emplace_back(trees[c]);
                    vis[c] = true;
                }
            }
            if(!vis[b]) {
                res.emplace_back(trees[b]);
                vis[b] = true;
            }
            a = b; // 以b为起始
        } while(a != left); // 转回起始点停下
        return res;
    }
};

• 时间复杂度：$O(n^2)$，判断每个点时都要遍历所有点，即判断$n$次过程中遍历$n$次。
• 空间复杂度：$O(n)$，标记每个点。

思路二：Graham算法

• 找到起始点后，还是用到上面的叉乘cross思路来判断极角大小，按极角排序得到初始遍历顺序。
• 同样需要考虑共线问题，若在凸壳的最后一条边上存在了共线的点，需从距离起始点最远的点开始考虑。因此需对排序好的数组尾部共线的元素翻转，得到最终遍历顺序。
• 用一个栈存储当前的凸壳，将前两个点直接放入栈中，从第三个点开始遍历判断是左拐（$cross<0$）还是右拐（$cross>0$）。
  • 若为当前点与上一条线（栈顶两个元素构成）是右拐的，说明栈顶点在形状内部，需弹出，然后考虑新的线与当前点的关系。
  • 否则（左拐和共线）暂时将当前点加入凸壳上。
• 遍历结束后，栈中即为最终构成的凸壳。

Java

class Solution {
    public int cross(int[] a, int[] b, int[] c) { // 叉乘
        return (b[0] - a[0]) * (c[1] - b[1]) - (b[1] - a[1]) * (c[0] - b[0]);
    }

    public int distance(int[] a, int[] b) { // 距离
        return (a[0] - b[0]) * (a[0] - b[0]) + (a[1] - b[1]) * (a[1] - b[1]);
    }

    // 交换两个点的位置，用于原地排序
    public void swap(int[][] trees, int i, int j) {
        int tmpx = trees[i][0], tmpy = trees[i][1];
        trees[i][0] = trees[j][0];
        trees[i][1] = trees[j][1];
        trees[j][0] = tmpx;
        trees[j][1] = tmpy;
    }

    public int[][] outerTrees(int[][] trees) {
        int n = trees.length;
        if(n < 4)
            return trees;
        
        int btm = 0; // 最靠下的点，作为起始点
        for(int i = 0; i < n; i++)
            if(trees[i][1] < trees[btm][1])
                btm = i;

        swap(trees, btm, 0);
        Arrays.sort(trees, 1, n, (a, b) -> {
            int polar = cross(trees[0], a, b);
            if(polar == 0) // 极角相同则按与起始点的距离由小到大
                return distance(trees[0], a) - distance(trees[0], b);
            else
                return -polar;
        }); // 按与起始点的极角由小到大排序
        // 末尾的共线点按距离由大到小排序
        int r = n - 1;
        while (r >= 0 && cross(trees[0], trees[n - 1], trees[r]) == 0)
            r--;
        for(int l = r + 1, h = n - 1; l < h; l++, h--)
            swap(trees, l, h);

        Deque<Integer> stack = new ArrayDeque<Integer>();
        stack.push(0);
        stack.push(1);
        for(int i = 2; i < n; i++) {
            int top = stack.pop();
            while(!stack.isEmpty() && cross(trees[stack.peek()], trees[top], trees[i]) < 0) // 右拐
                top = stack.pop(); // 更新top，也就丢弃了上一个top
            stack.push(top); // top放回去
            stack.push(i);
        }

        int sz = stack.size();
        int[][] res = new int[sz][2];
        for(int i = 0; i < sz; i++)
            res[i] = trees[stack.pop()];
        return res;
    }
}

• 时间复杂度：$O(n\log n)$，排序时间复杂度为$O(n\log n)$，处理栈中元素，至多每个元素各入栈出栈一次，时间复杂度为$O(2n)$。
• 空间复杂度：$O(n)$，快排所需栈空间为$O(\log n)$，用于存结果的栈至多需要$O(n)$。

C++

class Solution {
public:
    int cross(const vector<int> &a, const vector<int> &b, const vector<int> &c) { // 叉乘
        return (b[0] - a[0]) * (c[1] - b[1]) - (b[1] - a[1]) * (c[0] - b[0]);
    }

    int distance(const vector<int> &a, const vector<int> &b) { // 距离
        return (a[0] - b[0]) * (a[0] - b[0]) + (a[1] - b[1]) * (a[1] - b[1]);
    }

    vector<vector<int>> outerTrees(vector<vector<int>>& trees) {
        int n = trees.size();
        if(n < 4)
            return trees;

        int btm = 0; // 最靠下的点，作为起始点
        for(int i = 0; i < n; i++)
            if(trees[i][1] < trees[btm][1])
                btm = i;
        
        swap(trees[btm], trees[0]);
        sort(trees.begin() + 1, trees.end(), [&](const vector<int> &a, const vector<int> &b) {
            int polar = cross(trees[0], a, b);
            if(polar == 0) // 极角相同则按与起始点的距离由小到大
                return distance(trees[0], a) < distance(trees[0], b);
            else
                return polar > 0;
        }); // 按与起始点的极角由小到大排序
        // 末尾的共线点按距离由大到小排序
        int r = n - 1;
        while (r >= 0 && cross(trees[0], trees[n - 1], trees[r]) == 0)
            r--;
        for(int l = r + 1, h = n - 1; l < h; l++, h--)
            swap(trees[l], trees[h]);

        stack<int> stack;
        stack.emplace(0);
        stack.emplace(1);
        for(int i = 2; i < n; i++) {
            int top = stack.top();
            stack.pop();
            while(!stack.empty() && cross(trees[stack.top()], trees[top], trees[i]) < 0) { // 右拐
                top = stack.top();  // 更新top，也就丢弃了上一个top
                stack.pop();
            }
            stack.emplace(top); // top放回去
            stack.emplace(i);
        }

        vector<vector<int>> res;
        while(!stack.empty()) {
            res.emplace_back(trees[stack.top()]);
            stack.pop();
        }
        return res;
    }
};

• 时间复杂度：$O(n\log n)$，排序时间复杂度为$O(n\log n)$，处理栈中元素，至多每个元素各入栈出栈一次，时间复杂度为$O(2n)$。
• 空间复杂度：$O(n)$，快排所需栈空间为$O(\log n)$，用于存结果的栈至多需要$O(n)$。

思路三：Andrew算法

• 使用单调链算法，从边界开始逆时针遍历，找左拐（向外）的点，判断向左向右还是用cross。但是将最左和最右点相连将凸壳划分为上凸壳和下凸壳分别求出。
• 双关键字排序，x升序后y升序：
  • x升序：保证顺着一个方向可以画出一半边缘；
  • y升序：保证若将当前两点连线，其间所有点都可被围住。
• 用单调栈维护凸壳，思路类似Graham方法，看当前点和栈顶两个点的方向关系，不过二者遍历顺序不同（Graham按极角排序，Andrew按xy双关键字排序）。
• 无需考虑共线问题，因为已隐式地被按正确顺序考虑。
• 此处尝试直接用数组构建栈。

【vis数组仅用于记录前半部分已用过的点，而非处理过的点或凸包上的点，所以求后半部分时无需维护。且最终会转回起始点，所以不对起始点进行标记。】

Java

class Solution {
     public int cross(int[] a, int[] b, int[] c) { // 叉乘
        return (b[0] - a[0]) * (c[1] - b[1]) - (b[1] - a[1]) * (c[0] - b[0]);
    }

    public int[][] outerTrees(int[][] trees) {
        int n = trees.length;
        if(n < 4)
            return trees;
        
        // 双关键字排序
        Arrays.sort(trees, (a, b) -> {
            return a[0] == b[0] ? a[1] - b[1] : a[0] - b[0];
        });
        
        int top = 0;
        int[] stack = new int[n + 10];
        boolean[] vis = new boolean[n + 10];
        stack[++top] = 0; // 不标记起点，最后会转回来
        for(int i = 1; i < n; i++) { // 升序找下凸壳
            while(top >= 2) {
                if(cross(trees[stack[top - 1]], trees[stack[top]], trees[i]) < 0) // 右拐
                    vis[stack[top--]] = false;
                else
                    break;
            }
            stack[++top] = i;
            vis[i] = true;
        }
        int sz = top;
        for(int i = n - 1; i >= 0; i--) { // 降序找上凸壳
            if(vis[i])
                continue;
            while(top > sz) { // 避免删除已处理好的下凸壳
                if(cross(trees[stack[top - 1]], trees[stack[top]], trees[i]) < 0) // 右拐
                    top--;
                else
                    break;
            }
            stack[++top] = i;
        }

        int[][] res = new int[top - 1][2]; // 起点入栈两次
        for(int i = 1; i < top; i++)
            res[i - 1] = trees[stack[i]];
        return res;
    }
}

• 时间复杂度：$O(n\log n)$，排序时间复杂度为$O(n\log n)$，处理栈中元素，至多每个元素各入栈出栈一次，时间复杂度为$O(2n)$。
• 空间复杂度：$O(n)$，快排所需栈空间为$O(\log n)$，用于存结果的栈至多需要$O(n)$。

C++

class Solution {
public:
    int cross(const vector<int> &a, const vector<int> &b, const vector<int> &c) { // 叉乘
        return (b[0] - a[0]) * (c[1] - b[1]) - (b[1] - a[1]) * (c[0] - b[0]);
    }

    vector<vector<int>> outerTrees(vector<vector<int>>& trees) {
        int n = trees.size();
        if(n < 4)
            return trees;
        
        // 双关键字排序
        sort(trees.begin(), trees.end(), [&](const vector<int> &a, const vector<int> &b) {
            return a[0] == b[0] ? a[1] < b[1] : a[0] < b[0];
        });

        int top = 0;
        vector<int> stack(n + 10);
        vector<bool> vis(n + 10);
        stack[++top] = 0; // 不标记起点，最后会转回来
        for(int i = 1; i < n; i++) { // 升序找下凸壳
            while(top >= 2) {
                if(cross(trees[stack[top - 1]], trees[stack[top]], trees[i]) < 0) // 右拐
                    vis[stack[top--]] = false;
                else
                    break;
            }
            stack[++top] = i;
            vis[i] = true;
        }
        int sz = top;
        for(int i = n - 1; i >= 0; i--) { // 降序找上凸壳
            if(vis[i])
                continue;
            while(top > sz) { // 避免删除已处理好的下凸壳
                if(cross(trees[stack[top - 1]], trees[stack[top]], trees[i]) < 0) // 右拐
                    top--;
                else
                    break;
            }
            stack[++top] = i;
        }

        vector<vector<int>> res(top - 1, vector<int>(2));
        for(int i = 1; i < top; i++)
            res[i - 1] = trees[stack[i]];
        return res;
    }
};

• 时间复杂度：$O(n\log n)$，排序时间复杂度为$O(n\log n)$，处理栈中元素，至多每个元素各入栈出栈一次，时间复杂度为$O(2n)$。
• 空间复杂度：$O(n)$，快排所需栈空间为$O(\log n)$，用于存结果的栈至多需要$O(n)$。

总结

有亿点复杂，但能学个新算法 ，今天有点浪光搞了代码思路没整理好，明天搞完！
【最后是又拖了一天才搞好，着实有点复杂，逻辑不算很难，但实现中有很多小细节需要注意，比如排序函数的调用格式】

这几天着实又浪又忙……

欢迎指正与讨论！