HDU 4549 M斐波那契数列 (矩阵快速幂 + 费马小定理)

本文链接：https://blog.csdn.net/sizaif/article/details/77019189

M斐波那契数列

Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 3645 Accepted Submission(s): 1140

Problem Description

M斐波那契数列F[n]是一种整数数列，它的定义如下：

F[0] = a
F[1] = b
F[n] = F[n-1] * F[n-2] ( n > 1 )

现在给出a, b, n，你能求出F[n]的值吗？

Input

输入包含多组测试数据；
每组数据占一行，包含3个整数a, b, n（ 0 <= a, b, n <= 10^9 ）

Output

对每组测试数据请输出一个整数F[n]，由于F[n]可能很大，你只需输出F[n]对1000000007取模后的值即可，每组数据输出一行。

Sample Input

Sample Output

123

题意很明确, 求F(N)

一般求法肯定不行;

推公式写出F(1)=b F(2)=ab F(3)=ab^2 F(4)=a^2b^3 F(5)=a^3b^5 F(6)=a^5b^8 会发现对于 b的^ 而言是一个斐波那契数列而且是第 N 项 a的^是第N-1 项

所以转化成 F(N)= a^fib(n-1) * b^fib(n)

但是对于斐波那契数列而言后面的非常大已经超过long long 了而且效率也不高, 但是矩阵快速幂就可以在log(N) 内解决:

F(0)=0,F(1) =1 ,F(2) =3

这是斐波那契数列矩阵转换形式 F(0)=0,F(1) =1 ,F(2) =3

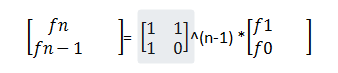
然后在利用快速幂 , 让我头疼不已的是一直WA 问题在于快速幂上, 因为数非常大可能会超;

所以得利用费马小定理:

假如p是质数，且gcd(a,p)=1，那么 a^(p-1)≡1（mod p），即：假如a是整数，p是质数，且a,p互质(即两者只有一个公约数1)，那么a的(p-1)次方除以p的余数恒等于1。

a^(p-1)≡1(mod p)

a^n= a^(n%(p-1)) %p 1000000007又是一个素数;

因此在求矩阵的时候需要 %(p-1) **************** 这里就是问题所在

代码:

#include <iostream>
#include <stdio.h>
#include <cmath>
#include <algorithm>
#include <cstring>

typedef long long ll;
const ll MOD=1000000007;
const int N= 12;
const int MAXN=2;
using namespace std;

struct Matrix{
	ll arr[N][N];
	void init()
	{
		memset(arr,0,sizeof(arr));
		for(int i=0;i<MAXN;i++)
			arr[i][i]=1;//初始化单位矩阵
	}
	void iinit()
	{
	    memset(arr,0,sizeof(arr));
	    arr[0][0]=arr[0][1]=arr[1][0]=1;
	}
}A;
Matrix mul(Matrix X,Matrix Y)// 矩阵乘法
{
	Matrix ans;
	for(int i=0;i<MAXN;i++)
		for(int j=0;j<MAXN;j++){
			ans.arr[i][j]=0;
			for(int k=0;k<MAXN;k++){
                ans.arr[i][j]+=X.arr[i][k]*Y.arr[k][j];
                ans.arr[i][j]%=(MOD-1);// 费马小定理应用
			}
		}
	return ans;
}
Matrix Q_pow(Matrix B,ll n)// ¾ØÕó¿ìËÙÃÝ
{
	Matrix ans;
	ans.init();
	while(n)
	{
		if(n&1)
			ans=mul(ans,B);
		n>>=1;
		B=mul(B,B);
	}
	return ans;
}
Matrix Add(Matrix a,Matrix b)  //(a+b)%mod 矩阵加法
{
    int i,j,k;
    Matrix ans;
    for(i=0;i<MAXN;i++)
        for(j=0;j<MAXN;j++)
        {
            ans.arr[i][j]=a.arr[i][j]+b.arr[i][j];
            ans.arr[i][j]%=MOD;
        }
    return ans;
}
Matrix Sum(Matrix a,int n)// 矩阵和
{
	int m;
	Matrix ans,pre;
	if(n==1) return ans;
	m=n/2;
	pre=Sum(a,m);
	ans=Add(pre,mul(pre,Q_pow(a,m)));
	if(n&1)
		ans=Add(ans,Q_pow(a,n));
	return ans;
}
ll Quick_pow(ll x,ll n)
{
    ll res=1;
    while(n)
    {
        if(n&1)
            res=(res*x)%MOD;
        x=(x*x)%MOD;
        n >>= 1;
    }
    return res;
}

int main()
{
    ll a,b,n;
    while(~scanf("%lld %lld %lld",&a,&b,&n))
    {
        Matrix ans;
        ans.iinit();
        if(n==0)
            printf("%lld\n",a);
//        else if(n==1)
//            printf("%lld\n",b);
        else
        {
            ans=Q_pow(ans,n-1);
            ll bx=ans.arr[0][0]; //fib(n)
            ll ay=ans.arr[1][0];// fib(n-1)
            ll res=0;
            res= ((Quick_pow(b,bx))*(Quick_pow(a,ay)))%MOD;
            printf("%lld\n",res%MOD);
        }
    }
}