信号与系统第二次试验：连续时间 LTI 系统的时域分析

前言

为了帮助同学们完成痛苦的实验课程设计，本作者将其作出的实验结果及代码贴至CSDN中，供同学们学习参考。如有不足或描述不完善之处，敬请各位指出，欢迎各位的斧正！

一、实验目的

1．学会运用 MATLAB 符号求解连续系统的零输入响应和零状态响应
2．学会运用 MATLAB 求解连续系统的冲激响应和阶跃响应

二、实验原理

信号一般是随时间而变化的某些物理量。按照自变量的取值是否连续，信号分为连续时间信号和离散时间信号，一般用f(t)和f(k)来表示。若对信号进行时域分析，就需要绘制其波形，如果信号比较复杂，则手工绘制波形就变得很困难，且难以精确。MATLAB强大的图形处理功能及符号运算功能，为实现信号的可视化及其时域分析提供了强有力的工具。
LTI连续系统可用线性常系数微分方程来描述，即：

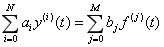
其中，ai(i=0,1,…，N)和bi(i=0,1,…，M)为实常数。该系统的完全响应由零输入响应yzi(t)和零状态响应yzs(t)两部分组成。
MATLAB符号工具箱提供了dsolve函数，可实现常系数微分方程的符号求解，其调用格式为：

dsolve('eq1,eq2,…','cond1,cond2,…','v')

其中，参数eq1,eq2…表示各微分方程，它与MATLAB符号表达式的输入基本相同，微分或导数的输入是用Dy,D2y,D3y,…来分别表示y的一阶导数，y的二阶导数，y的三阶导数…；参数cond1，cond2，…表示个初始条件或起始条件；参数v表示自变量，默认为变量t。可利用dsolve函数来求解系统微分方程的零输入响应和零状态响应，进而求出完全响应。
在连续时间LTI系统中，冲激响应和阶跃响应是系统特性的描述，对它们的分析是线性系统中极为重要的问题。输入为单位冲激函数δ(t)所引起的零状态响应称为单位冲激响应，简称冲激响应，用h(t)表示；输入为单位阶跃函数u(t)所引起的零状态响应称为单位阶跃响应，简称阶跃响应，用g(t)表示。

三、实验环境

硬件：装有Windows 10系统的PC机
软件：MATLAB 2018b

四、实验内容和步骤及实验数据

clear;clc;
eq1='D2y+3*Dy+2*y=Dx+3*x';
eq2='x=exp(-3*t)*heaviside(t)';
cond='y(0)=1,Dy(0)=2';
cond1='y(-0.01)=0,Dy(-0.01)=0';
dsolve(eq1,eq2,cond1);
eq3='D2y+3*Dy+2*y=0';
disp("零输入:");
a=dsolve(eq3,cond);
a=simplify(a)
disp("零状态:");
simplify(ans.y)
disp("全响应:");
simplify(a+ans)

零输入:
a =
exp(-2t)(4exp(t) - 3)
零状态:
ans =
(exp(-2t)(exp(t) - 1)(sign(t) + 1))/2
全响应:
ans =
exp(-2t)(4exp(t) - 3) + (exp(-2t)(exp(t) - 1)(sign(t) + 1))/2

clear;clc;
t=0:0.01:4;
sys=tf([1],[1,3,2]);
h=impulse(sys,t);
g=step(sys,t);
subplot(211)
plot(t,h),grid on
xlabel('Time(sec)'),ylabel('h(t)')
title('冲激响应')
subplot(212)
plot(t,g),grid on
xlabel('Time(sec)'),ylabel('g(t)')
title('阶跃响应')

五、实验结论

六、实验总结

单位阶跃信号：heaviside(t)或 stepfun(t,t0)，其中，t是以向量形式表示的变量，t0表示信号发生突变的时刻。
LTI连续系统可用线性常系数微分方程来描述，即：

其中，ai(i=0,1,…，N)和bi(i=0,1,…，M)为实常数。该系统的完全响应由零输入响应yzi(t)和零状态响应yzs(t)两部分组成。
MATLAB符号工具箱提供了dsolve函数，可实现常系数微分方程的符号求解，其调用格式为：

dsolve('eq1,eq2,…','cond1,cond2,…','v')

在MATLAB中，对于连续LTI系统的冲激响应和阶跃响应的数值解，可分别用控制系统工具箱提供的函数impulse和step来求解。其语句格式分别为：

y=impulse(sys,t);
y=step(sys,t);

在遇到问题时，多使用doc函数进行查询