快速排序
整体思路：
- 划分，找基准点x = nums[(l + r) >> 1]这个最好理解
- 用双指针两端向中间遍历，在右边找到一个比x小的数，在右边找到一个比x大的数，再交换。重复直到i <= j。
这种方法与教材不同的是把基准点也放进去继续递归了 - 分别递归区间(l, j)和(j + 1, r)
归并排序
- 边界条件l < r，二分mid = l + r >> 1，分别递归区间(l, mid)和(mid + 1, r)
- 递归到最底层，自底向上对当前划分的两个数组进行排序合并
第k小元素
如果待排序数组的规模较小则直接采用堆排序，若数组规模较大则采用以下方法
- 将n个元素分为n / 5组取上界，并且将每组的5个元素排序
- 求出n / 5组每一组的中位数得到数组A
- 求数组A的中位数得到mid为划分基准，将数组划为3种情况：A1 = 小于mid；A2 = 等于mid；A3 = 大于mid
if len(A1) >= k：第k小元素在A1中，这时递归查找即可
elif：len(A1) + len(A2) >= k：mid即为第k小元素
else：在A3中递归寻找第k - len(A1) + len(A2)小的元素
最近点对
- 计算得到所有点x坐标的中位数m，以x = m将点划分为左右两部分l和r
- 先递归的求得左右两部分的最小距离d1和d2，也就是先递归到最底层
- d = min(d1, d2)，得到区间(m - d, m + d)，在该区间寻找是否存在一个点p1在左区间一个点p2在右区间使得他们之间的距离d3小于d。如果存在则d3为最终结果，否则d为最终结果。
- 根据鸽笼原理可证明在区间(m - d, m + d)内每个点最多只需要比较6个点就能得到距离最近的点
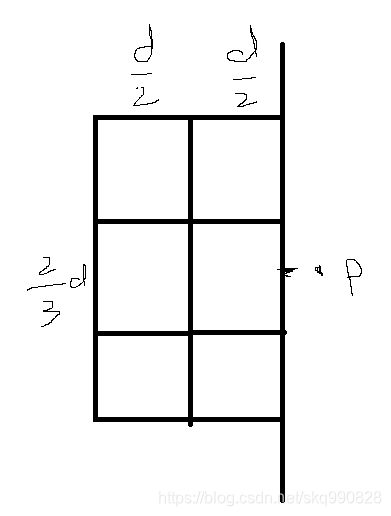
右边的点p只需要和左边d * 2d的矩形中的点比较即可得到与p最近的那个点
又因为左区间所有点的的距离最小为d，根据鸽舍原理每个矩形最多只能有一个点在内，也就是说p最多只需要和6个点比较就能找到左边与其距离最小的那个点。
寻找凸包
- 寻找到最下且最左的点P0，将这个这个点与其他n - 1个点连线，并将这n - 1个点按照其与P0的角度排序
- 将P0,P1,P2压入一个栈中，从P2开始判断接下来的点Pi，如果Pi不能与栈中的点构成凸包，则弹出栈中元素，直至能构成凸包再把Pi加入栈中
矩阵连乘
矩阵连乘问题具有最优子结构和子问题重叠的性质，所以可以用动态规划来解决
令
f
[
i
]
[
j
]
f[i][j]
f[i][j]为矩阵i连乘到矩阵j的代价，
w
[
i
]
w[i]
w[i]保存第一个矩阵的行列以及剩余n - 1个矩阵的行。
由于如果两个矩阵分别为A * B和C * D，它们相乘的代价为A * B * D
所以用k来分割矩阵i到矩阵j，则有
f
[
i
]
[
j
]
=
m
i
n
(
f
[
i
]
[
k
]
+
f
[
k
+
1
]
[
j
]
+
w
[
i
−
1
]
∗
w
[
k
]
∗
w
[
j
]
)
f[i][j] = min(f[i][k] + f[k + 1][j] + w[i - 1] * w[k] * w[j])
f[i][j]=min(f[i][k]+f[k+1][j]+w[i−1]∗w[k]∗w[j])
k的取值为i ~ j - 1
枚举的方法为：
- 先遍历区间长度len
- 遍历区间的左节点i,则右节点为i + len - 1
- 遍历分割点k
问题的初始值为 f [ i ] [ i ] = 0 f[i][i] = 0 f[i][i]=0i取值为1~n，因为单一矩阵不需要相乘，代价为0
问题的返回值为 f [ 1 ] [ n ] f[1][n] f[1][n]，即n个矩阵相乘的最小代价
钢条切割
f
[
i
]
=
m
a
x
(
f
[
i
−
j
]
+
v
[
j
]
)
f[i] = max(f[i - j] + v[j])
f[i]=max(f[i−j]+v[j]),j为价格表中的钢条长度
初始值为：f[0] = 0
实现方法为先令
t
e
m
p
=
f
l
o
a
t
(
′
−
i
n
f
′
)
temp = float('-inf')
temp=float(′−inf′)，再枚举j，每次取较大的值
最后令
f
[
i
]
=
t
e
m
p
f[i] = temp
f[i]=temp
最长公共子序列
f [ i ] [ j ] = 0 ; i = 0 , j = 0 f [ i ] [ j ] = f [ i − 1 ] [ j − 1 ] + 1 ; i , j > 0 且 x i = y j f [ i ] [ j ] = m a x ( f [ i ] [ j − 1 ] , f [ i − 1 ] [ j ] ) ; i , j > 0 且 x i ! = y j f[i][j] = 0; i = 0, j = 0 f[i][j] = f[i - 1][j - 1] + 1; i, j > 0且xi = yj f[i][j] = max(f[i][j - 1], f[i - 1][j]); i, j > 0且xi != yj f[i][j]=0;i=0,j=0f[i][j]=f[i−1][j−1]+1;i,j>0且xi=yjf[i][j]=max(f[i][j−1],f[i−1][j]);i,j>0且xi!=yj
最优二叉搜索树
f [ i ] [ j ] = f [ i ] [ k − 1 ] + f [ k + 1 ] [ j ] + w [ i ] [ j ] w [ i ] [ j ] = w [ i ] [ j − 1 ] + p [ j ] + q [ j ] f o r i i n r a n g e ( 1 , n + 1 ) : f [ i ] [ i − 1 ] = q [ i − 1 ] w [ i ] [ i − 1 ] = q [ i − 1 ] f[i][j] = f[i][k - 1] + f[k + 1][j] + w[i][j] w[i][j] = w[i][j - 1] + p[j] + q[j] for i in range(1, n + 1): f[i][i - 1] = q[i - 1] w[i][i - 1] = q[i - 1] f[i][j]=f[i][k−1]+f[k+1][j]+w[i][j]w[i][j]=w[i][j−1]+p[j]+q[j]foriinrange(1,n+1):f[i][i−1]=q[i−1]w[i][i−1]=q[i−1]
流水作业调度问题
- 先把所有作业的ai和bi放在一起，从这之中选个最小的
- 如果是bi的话这个作业i就放最后，如果是ai的话这个作业就放最前，把这个已经安排好的作业从作业集中删除。3. 重复上述步骤即可。
活动选择问题
为了使活动安排尽可能的多，每次选择结束时间最早的活动
满足最优子结构和贪心选择性
最短路径问题
- 令S = {v0}，T = {其他顶点}，dist[i]为v0带vi的距离
- 从T选择一个距离v0最小的点加入S中，修改dist使得每一个vi到v0的距离都是最短路径
- 重复2，使得点全部加入S为止
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
