MATLAB 匿名函数详解（超级全面）

匿名函数与之相对的即为需要.m文件存储的命名函数，匿名函数可以在任意地方定义(包含命令行窗口)，且由于没有固定的名称，函数是可以像变量一样被传递的。以下详细讲解一下MATLAB中不可或缺的一部分具体能够怎么用：

先给个目录，千万不要被吓到：

---

1 匿名函数的生成

1.1基础生成

(例)

f=@(x)x^2;

注：匿名函数所输入的参数可以是向量形式，只需将其中部分运算更改为点运算即可：

f=@(x)x.^2;
f(1:5)

ans =
1 4 9 16 25

也可以这么写，但除了3.3所示情况外不推荐：

f=@(x)arrayfun(@(x)x^2,x)
f(1:5)

当然eval函数cellfun,structfun等一系列常用函数也是可以在匿名函数中用到的。

同时逻辑运算对于匿名函数也成立，如下：

f=@(x)x>3&x<5

分段函数：

f=@(x)(x>3)*5+(x<=3)*4

1.2 多参数匿名函数

(例)

f=@(x,y)x^2+y;

1.3 含定参匿名函数

详见2.4部分
(例)

a=5;
f=@(x)a*x^2;

注意，即使在后来改变a的值函数f内的a也不会改变,例：

a=5;
f=@(x)a*x^2;
a=1;
f(2)

ans=20，注意此处求得数值为20 而不是4
此时若是存储该匿名函数，例：

a=5;
f=@(x)a*x^2;
save func1.mat f;

此时存储的匿名函数仍旧是包含参数的，可以通过以下两种方式使用：

load('func1.mat')
f(2)

func=load('func1.mat');
func.f(2)

1.4 sym转匿名函数

sym格式的公式可通过如下方式生成匿名函数(第一种较慢)

syms x
a=x^2+x;
f=matlabFunction(a)

或

a=sym(x^2+x);
f=matlabFunction(a)

1.5 字符串转匿名函数

方式如下：

a='@(x) x^2+2*x';
b=str2sym(a);
f=matlabFunction(b)

注：MATHWORK近期又出了str与句柄的转换函数，
比较新的版本可用下面的方式：

str='@(x)7*x-13';
fh=str2func(str)

1.6 函数工厂（匿名函数的自动生成）

1.6.1 已知参数个数

在一些项目中，需要根据不同参数生成不同匿名函数，
例如下面为a,b,c三个参数不同时能够自动生成不同匿名函数的生成函数：

方式一(借助sym):

function func=funcFactory(a,b,c)
    syms x
    func=matlabFunction(a*x^2+b*x+c);
end

方式二(借助字符串):

function func=funcFactory(a,b,c)
    str=['@(x)',num2str(a),'*x^2+',num2str(b),'*x+',num2str(c )];
    func=matlabFunction(str2sym(str));
end

使用方式：

funcFactory(1,2,3)

ans =
包含以下值的 function_handle:
@(x)x.*2.0+x.^2+3.0

1.6.2 未知参数个数

未知参数个数其变量可以设置为
x1,x2,x3…xn或者
v1,v2,v3…vn这样的形式

如下为一不固定长度的函数生成其，其中v为不定长度的参数

function func=funcFactory(v)
f=0;
for i=1:length(v)
    xn=str2sym(['x',num2str(i)]);
    f=f+v(i)*xn;
end
func=matlabFunction(f);
end

使用方式：

funcFactory([1 2 3 4 3])

ans =
包含以下值的 function_handle:
@(x1,x2,x3,x4,x5)x1+x2.*2.0+x3.*3.0+x4.*4.0+x5.*3.0

当然由于syms变量可以向量化生成，该例子显然也可以向量化：

function func=funcFactory(v)
f=sym('x',[1,length(v)]);
f=f*v';
func=matlabFunction(f);
end

1.7 拟合结果转匿名函数

(例)

x=[2 2.5 3 3.5 4 4.5 5 5.5 6];
y=[41 38 34 32 29 28 25 22 20];
p=polyfit(x,y,3);
f=matlabFunction(poly2sym(p ))

f =
包含以下值的 function_handle:
@(x)x.(-8.57e+2./5.4e+1)+x.^{2.*(2.56e+2./9.9e+1)-x.}3.(5.8e+1./2.97e+2)+7.05e+2./1.1e+1

1.8 匿名函数的引用

如下所示f2为f1的倒函数

f1=@(x)x^2;
f2=@(x)1/f1(x)
f2(2)

与前面定参匿名函数相似，此处f1也可被看作固定参数，即使之后改变也不会对f2造成影响

1.9 匿名函数的传递

可以将匿名函数像是变量一样传递：

f1=@(x)x.*2+x.^3;

f2=f1;
f2(2)

ans = 12

1.10 无参数匿名函数

(例)

e=@()exp(1);
e()
t=@()datestr(now);
t()

ans =
2.7183
  \,
ans =
‘04-Mar-2021 20:18:30’

1.11 可变长度输入参数列表

想不到叭varargin这玩意也能用

f1=@(varargin)length([varargin{:}]);
f1({'slandarer',[1,2;3,4],5})

ans = 3

1.12 多返回值匿名函数

使用deal函数分发输出即可：

f=@(x)deal(x^2,x^3)
[a,b]=f(3)

f =
包含以下值的 function_handle:
@(x)deal(x^2,x3)
  \,
a =
9
  \,
b =
27

1.13 命名函数转化为匿名函数

其实这么名称不够严谨，应该叫函数句柄对命名函数的复制

fsum=@ mysum
fsum(1,2)
function c=mysum(a,b)
	c=a+b;
end

fsum =
包含以下值的 function_handle:
@mysum
  \,
ans =
3

---

2 匿名函数的结构

2.1 匿名函数数组

f={@(x)x^2;@(x)3*x;@(x)x^x}
f{1}(2)

f =
3×1 cell 数组
{@(x)x^2}
{@(x)3*x}
{@(x)x^x}
  \,
ans =
4

2.2 匿名函数结构体

func.f1=@(x)x^2;
func.f2=@(x)3*x;
func.f3=@(x)x^x

调用方式：

func.f1(2)
func.('f1')(2)

func =
包含以下字段的 struct:
f1: @(x)x^2
f2: @(x)3*x
f3: @(x)x^x
  \,
ans =
4

2.3 匿名函数的非标量结构体数组

func(1).f=@(x)x^2;
func(2).f=@(x)3*x;
func(3).f=@(x)x^x;

func(1).f(2)

ans =
6

2.4 functions函数使用

functions函数可以获取匿名函数信息，对于1.3中的例子来说

a=5;
f=@(x)a*x^2;

coe=functions(f)
coe.workspace{1}

coe =
包含以下字段的 struct:
function: ‘@(x)a*x^2’
type: ‘anonymous’
file: ‘E:\bin\匿名函数\Untitled.m’
workspace: {[1×1 struct]}
within_file_path: ‘’

ans =
包含以下字段的 struct:
a: 5

可以发现a是被存在函数信息中的
同样对于1.8的例子来说：

f1=@(x)x^2;
f2=@(x)1/f1(x);
coe=functions(f2)
coe.workspace{1}

coe =
包含以下字段的 struct:
function: ‘@(x)1/f1(x)’
type: ‘anonymous’
file: ‘E:\bin\匿名函数\Untitled2.m’
workspace: {[1×1 struct]}
within_file_path: ‘’

ans =
包含以下字段的 struct:
f1: @(x)x^2

2.5 局部命名函数的匿名函数列表

localfunctions函数能够获取该m文件文件所有function创建函数，并构建匿名函数列表：

fh=localfunctions

function y=f1(x)
y=sqrt(x)+x^2;
end

function y=f2(x)
y=sqrt(x)+cos(x);
end

function y=f3(x)
y=sqrt(x)+sin(x);
end

fh =
3×1 cell 数组
{@f1}
{@f2}
{@f3}

2.6 特殊结构匿名函数

将各种结构组合起来能够得到一些很有意思的写法：
注：此2.6节源自知乎大佬Falccm

https://www.zhihu.com/question/45621009/answer/99714353

递归匿名函数(斐波那契数列):
通过定义一个匿名函数数组，再用另一个匿名函数在不同条件下调用该数组的不同部分，就能实现在不陷入无限递归的情况下进行递归调用：

f={@(f,n)1 @(f,n)f{(n>3)+1}(f,n-1)+f{(n>4)+1}(f,n-2)};
fib=@(n)f{(n>2)+1}(f,n);
fib(20)

ans =
6765

匿名if函数:
巧用varargin函数

iff = @(varargin)varargin{find([varargin{1:2:end}],1)*2};

x = 3;

iff(x<1,1,x<2,2,x<3,3,x<4,4,x<5,5)

ans =
4

---

3 匿名函数的使用

3.1 以匿名函数为参数

f1=@(x,y)max(x);
opt(f1,1,2)
function c=opt(f,a,b)
c=f(a,b);
end

注下面的写法不适用于匿名函数，仅适用于function建立的函数

f1=@(x,y)max(x);
opt('f1',1,2)
function c=opt(f,a,b)
c=f(a,b);
end

3.2 调用其它文件匿名函数

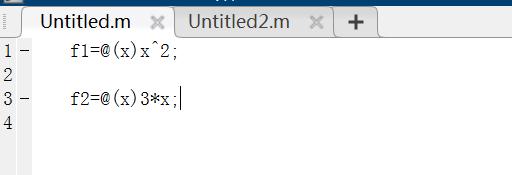
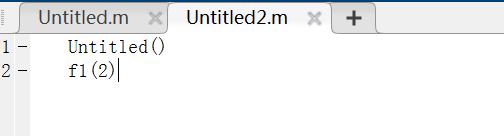
3.3 使用匿名函数表示隐函数

例如有一隐函数：
$$(e^y+x^y{)}^{\frac{1}{y}}-x^{2}y=0$$
可将其用匿名函数表示为：

y=@(x)fzero(@(y)(exp(y)+x^y)^(1/y)-x^2*y,1);

y(1)

ans =
2.7779

这种写法每次只能输入一组变量，要进行向量运算，需要使用arrayfun辅助，写作如下格式：

Y=@(x)arrayfun(@(xx)fzero(@(y)(exp(y)+xx^y)^(1/y)-xx^2*y,1),x);

Y(1:5)

ans =
2.7779 1.1055 0.7759 0.6284 0.5425

3.4 绘图匿名函数

还有一些奇奇怪怪的用法，例如。。。。绘图

x=-2:0.1:2;y=-2:0.1:2;
f=@(x,y)plot(x,y.^2);
f(x,y)

多个绘图命令用中括号括起来并用分号隔开：

x=-2:0.1:2;y=-2:0.1:2;
f=@(x,y)[plot(x,y.^2,'-o','LineWidth',1.8);title('x^2','FontSize',14);xlabel('x','FontSize',13)];
f(x,y)