Leetcode1105.填充书架（理解动态规划思路）_假设一共要选出 n 本书放在书架上,并且书的种类有 m 种,包括天文的、计算机的、-CSDN博客

本文链接：https://blog.csdn.net/snailbuster/article/details/98311032

博客详细解释了如何使用动态规划解决LeetCode上的填充书架问题，重点在于理解动态规划的状态转移和优化思路。作者指出，动态规划的关键是找到最优解并尝试将新书与已有的最优排列组合，以求得最小的书架总高度。通过迭代和双重循环，逐步更新状态并寻找最佳解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

原题：
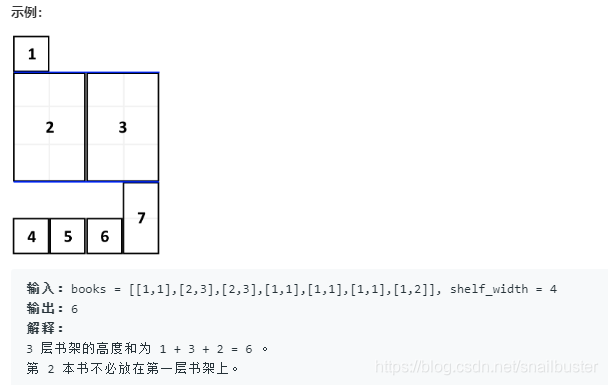
附近的家居城促销，你买回了一直心仪的可调节书架，打算把自己的书都整理到新的书架上。你把要摆放的书 books 都整理好，叠成一摞：从上往下，第 i 本书的厚度为 books[i][0]，高度为 books[i][1]。按顺序将这些书摆放到总宽度为 shelf_width 的书架上。先选几本书放在书架上（它们的厚度之和小于等于书架的宽度 shelf_width），然后再建一层书架。重复这个过程，直到把所有的书都放在书架上。需要注意的是，在上述过程的每个步骤中，摆放书的顺序与你整理好的顺序相同。例如，如果这里有 5 本书，那么可能的一种摆放情况是：第一和第二本书放在第一层书架上，第三本书放在第二层书架上，第四和第五本书放在最后一层书架上。每一层所摆放的书的最大高度就是这一层书架的层高，书架整体的高度为各层高之和。以这种方式布置书架，返回书架整体可能的最小高度。
在这里插入图片描述