向量组极大无关组和向量组的秩

向量组的极大无关组定义

极大无关组包含两层含义：1 极大性，2无关性。

1 线性无关向量组的极大无关组就是其本身；

2 向量组与其极大无关组等价；

3 同一个向量组的极大无关组不唯一，但它们之间是等价的。

 向量组的秩定义

 

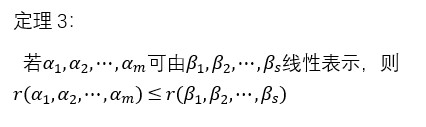
 推论：等价的向量组有相同的秩。

但是：有相同秩的两个向量组不一定等价。

向量组的秩的求法

行秩：矩阵行向量组的秩；列秩：矩阵列向量组的秩。

定理4：矩阵的行秩与列秩相等，为矩阵的秩。

推论：向量组的秩与该向量组所构成的矩阵的秩相等。

求向量组秩的方法：先将向量组构成一个矩阵，然后求矩阵的秩，这个秩就是向量组的秩。

极大无关组的求法

列摆行变换法：将向量按照列摆放，组成一个矩阵，然后对矩阵做初等行变换，化为梯形阵，然后从列中挑出与秩相同数量的列向量，得到极大无关组。

也可以使用行摆列变换。