概率论基础回顾
概率的认识
存在随机变量
X
,假设
问题来了,假设
X
是连续型随机变量,这里概率怎么来理解?
累计分布函数
- ϕ(x) 一定是单增函数
- min(ϕ(x))=0,max(ϕ(x))=1
- 将值域为 [0,1] 的某函数 y=f(x) 看成 y 事件的累积概率
- 若
y=f(x) 可导,则 p(x) 为某概率密度函数
思考一下,累积分布函数有啥用?
古典概率
古典概率通常又叫事前概率,是指当随机事件中各种可能发生的结果及其出现的次数都可以由演绎或外推法得知,而无需经过任何统计试验即可计算各种可能发生结果的概率。
实际问题:
某班上有50位同学,至少有2人生日相同的概率是多少?
条件概率
全概率公式
贝叶斯公式
实际问题:
8支步枪中有5支已校准过,3支未校准。一名射手用校准过的枪射击,中靶概率为0.8;用未校准的枪射击,中靶概率为0.3;现从8支枪中随机取一支射击,结果中靶。求该枪是已校准过的概率。
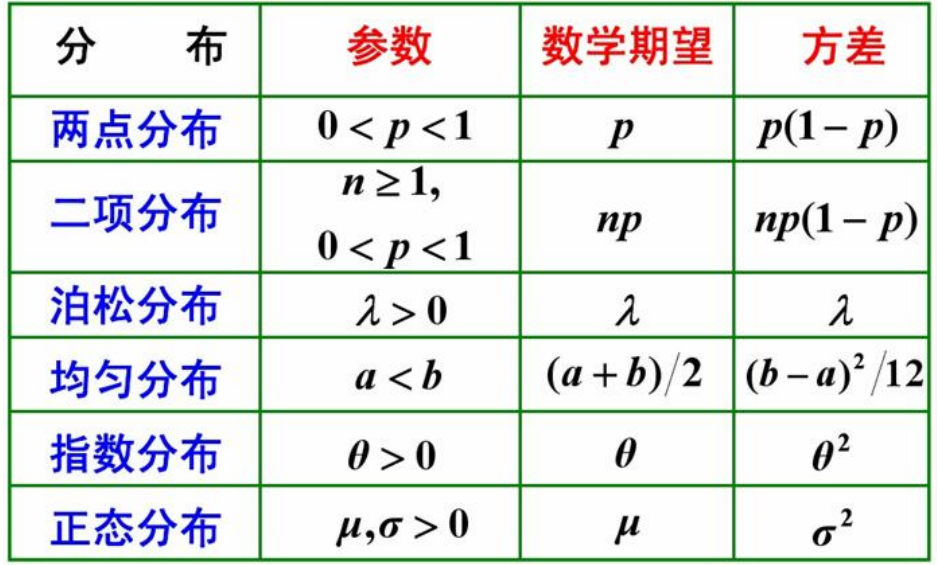
分布
离散型分布
伯努利分布、二项分布、几何分布和负二项分布、泊松分布
http://blog.csdn.net/zlbflying/article/details/47777943
连续型分布
均匀分布、指数分布、正态分布、
Beta
分布
思考:
二项分布->泊松分布?
n很大,p很小的二项分布,可近似为泊松分布
泊松分布与指数分布的联系?
泊松分布是单位时间内独立事件发生次数的概率分布,指数分布是独立事件的时间间隔的概率分布。
这么多分布,意义在哪?
极限定理
切比雪夫不等式
设随机变量X的期望为
μ
,方差为
σ2
,对于任意正数
ϵ
,有:
切比雪夫不等式说明, X 的方差越小, 事件
大数定理
令
X1
,
X2
,
X3
,……,
Xi
……是独立随机变量序列,
E(Xi)
=
μ
,
Var(Xi)=σ2
,令
X¯¯¯n=n−1∑ni=1Xi
,那么对任意的
ϵ
>0,当n->
∞
时,
证明过程可参考切比雪夫不等式
思考:
大数定理有啥用?
Eg:计算积分
I(f)=∫10f(x)dx
,假设
f(x)
异常复杂,怎么计算呢?
采用蒙特卡洛方法进行近似计算,生成[0,1]上独立的均匀随机变量,即
X1,X2,…,Xn
,然后计算
根据大数定理,上述结果接近于 E[f(x)]
中心极限定理
设随机变量
X1
,
X2
,
X3
……互相独立,服从同一分布,并且具有相同的期望
μ
和方差
σ2
,则随机变量
的分布收敛到标准正态分布。
中心极限定理的表述有很多种,这种我认为是比较好理解的,在实际问题处理中,很多随机变量分布都被认为是服从正态分布的,比如说线性回归中误差的分布。
实例:
大量存在的两点分布Bi(1,p),其中,Bi发生的概率为0.01,即p=0.01。取其中的n个,使得发生的个数除以总数的比例落在区间(0.0099,0.0101),则n至少是多少?
关于估计
样本的矩
k
阶原点矩:
k 阶中心距
矩估计的原理
样本的
k
阶矩等于总体的
实例:
在正态分布的总体中采样得到
n
个样本:
极大似然估计
http://blog.csdn.net/zlbflying/article/details/48474837
实例:
若给定一组样本 X1,X2,X3 …… Xn ,已知它们来自于高斯分布 N(μ,σ) ,试估计参数 μ , σ 。
假设检验
假设检验不再分享,原因在于在论文中使用到的概率较小,且假设检验主要用在对总体估计结果是否可信的判断上,大家参考概率论书籍即可。
卡方检验
这里单拿出卡方检验,卡方检验是在试验中用途非常广泛的一种检验方法,主要是比较两个及两个以上样本率( 构成比)以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。
实例:
假设你是一家赌场的老板,你怀疑有个赌客对骰子做了手脚。你已经将赌客抓了起来并没收了骰子。现在你必须证明他的骰子是有问题的。然后你掷了60次,记录如下:
点数 1 2 3 4 5 6
频数 8 9 19 6 8 10
用上述结果计算一下卡方统计量的值等于多少?






















 9711
9711

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








