离散型概率分布之一——二项分布

学习机器学习的过程中，不可避免会遇到很多概率统计知识，大多都是记得自己以前学过，但是具体知识点怎么都想不起来的。所以打算做一个系列的整理，首先从最简单的二项分布开始。

由于知识点呈递进关系，就不强行列一个目录出来了。

出于从最基础的知识点开始学起的想法，首先要了解的知识点是，什么是分布？具体来说，应该是什么是概率分布？

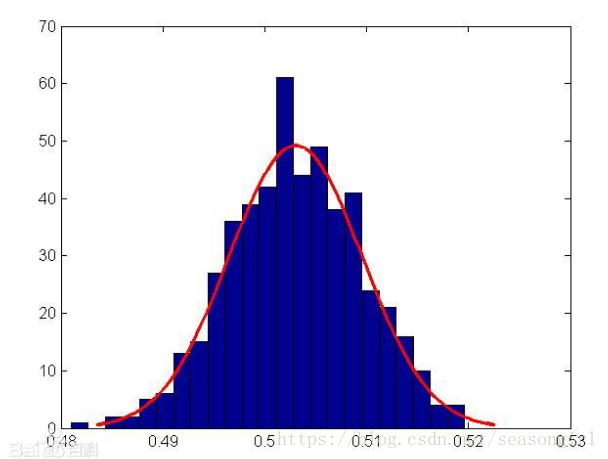
简单来说，就如上面的柱状图，图中每一个小柱子的高度，即为一个对应变量的概率分布，而整个统计图将所有随机变量对应的概率呈现出来，即为事件所有可能发生结果的概率分布。

了解完了什么是概率分布，接下来就可以开始了解概率分布分哪几种了。简单来说，按照随机变量的数据类型，可以分为两种，一种是离散型随机变量对应的概率分布，称为离散型概率分布，今天要讲的二项分布，以及后面要讲的泊松分布和几何分布，就都是离散型概率分布。 另一种，就是连续型概率分布，也即连续型随机变量对应的概率分布，典型的连续型概率分布，就是大名鼎鼎的正态分布，后面的博客中也将做出相应整理。

二项分布是什么？

对于这个问题，我想转化成——什么样的分布才是二项分布？

满足以下三个条件的分布，就是二项分布：

（1）做某件事情的次数（也叫试验次数）是固定的，用n表示。例如，抛硬币3次，求婚101次等。

（2）每一次事件都有两个可能的结果（成功，或者失败）。例如每次求婚都有两种可能结果，被接受（成功），被拒绝（失败）。

（3）每一次成功的概率都是相等的，成功的概率用p表示。

你感兴趣的是成功x次的概率是多少。那么就可以用二项分布的公式快速计算出来了。

知道了二项分布是什么，那么如何计算符合二项分布事件的概率呢？

很简单，用如下公式就可以计算出来。

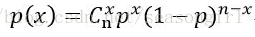
其中，p表示成功的概率，x表示成功的次数。

由于前面一篇博客讲了一下如何计算数学期望，所以这里也提一下如何计算二项分布的数学期望。

二项分布的数学期望E(x)=np

同样也提一下二项分布的标准差 

参考资料

[1]https://baike.baidu.com/item/%E4%BA%8C%E9%A1%B9%E5%88%86%E5%B8%83/1442377?fr=aladdin

[2]https://www.zhihu.com/question/36214010/answer/208718886

[3]https://baike.baidu.com/item/%E6%A6%82%E7%8E%87%E5%88%86%E5%B8%83/828907?fr=aladdin