先验概率、最大释然估计(MLE)与最大后验估计(MAP)

前言

在数据分析和机器学习中，估计是一个很重要的内容，这里着重介绍下极大似然估计与极大后验估计。

最大似然估计(MLE)

    最大似然估计是模型已定，参数未定时的一种估计方法。比如说对于抛硬币而言，模型已定，可以看做是多个伯努利实验，我们所不知道的是这个硬币正面朝上的概率$p$，所以我们的任务就是估计$p$的值。极大似然估计的思想是，对于已经给定的一些观测数据，参数$p$的取值应使得取得这些观测数据的概率最大。
    再以上面抛硬币为例，假设10次实验，7次正面朝上，此时根据极大似然估计$p$的取值应该为$7 \over 10$，具体计算过程一会给出。
    OK，这里总结出极大似然估计的一般过程。首先极大似然估计的前提是样本的采样是独立同分布的，假设现在得到的采样结果是$x_1$,$x_2$,$x_3$,$x_4$,$x_5$……，给定参数$\theta$，则取得该采样结果的联合概率为：

$$f(x_1,x_2,x_3,…，x_n;\theta)=f(x_1;\theta)\times f(x_2;\theta)\times …\times f(x_n;\theta)$$
$$L(\theta | x_1,x_2,…,x_n)=\prod_{i=1}^n f(x_i | \theta)$$
为了求得 $\theta$的值使得 $L(\theta | x_1,x_2,…,x_n)$取得极大值，而连乘形式通常很难求值，因此一般情况下会把连乘转化成连加，即会求 $L$的对数，如下所示：
$$lnL(\theta | x_1,x_2,…,x_n)=\sum_{i=1}^n lnf(x_i|\theta)$$
此时 $x_i$是已知量，只有参数 $\theta$是未知量，因此对 $\theta$求导。
$${dlnL(\theta) \over d\theta} = 0$$
求出 $\theta$的值即可。

特殊情况下，$L(\theta)$是一个递增函数或者其它比较简单的形式，我们无需进行求对数，只需直接判断即可。

现在对开头的抛硬币例子进行解释，我们可以判定每次抛硬币正面朝上的概率为$f(x = 1|p) = p^x \times (1-p)^{(1-x)}$，则10次实验做完联合概率为
$L(x_1,x_2,…，x_{10} | p) = p^{x_1}*p^{x_2}*…p^{x_{10}} *(1-p)^{(1-x_1)}*…(1-p)^{(1-x_{10})} = \prod_{i=1}^{10} p^{x_i} \times (1-p)^{(1-x_i)}$
对其进行求对数

$$lnL(x_1,x_2,…，x_{10} | p)= 7 * lnp +３*ln(1-p)$$
再对 $p$进行求导：
$${dlnL(\theta) \over d p} = {7 \over p} - {3 \over (1-p)}=0$$
求解得到 $p={7 \over 10}$

最大后验估计(MAP)

    最大后验估计与最大似然估计是类似的，只是这里加入了先验概率，我们在计算上述的抛硬币的试验时，并没有考虑硬币本身的因素，即$p$可能也是符合一个分布的。根据贝叶斯理论：

$$p(\theta | X) = {p(X | \theta) \times p(\theta) \over \sum_{\theta_i} p(X| \theta_i) \times p(\theta_i)}$$
这里的$p(\theta)$是参数$\theta$的先验概率，$p(\theta | X)$是后验概率，而$p(X|\theta)$就是我们上面提到的似然函数。在最大似然估计中，我们并没有考虑$p(\theta)$，即我们假设$p$是一个固定值，但实际上，参数$p$可能并不是固定的，它只是取某些值可能性比较大。因此我们只要将似然函数乘以先验概率然后取最大即可。
    仍以上面抛硬币来举例，这里以$Beta$分布来估计参数$p$的值，$Beta$分布是一个使用率非常高的分布，它根据$\alpha$和$\beta$的值可以使$Beta(\alpha, \beta)$取不同的值，如下图所示。

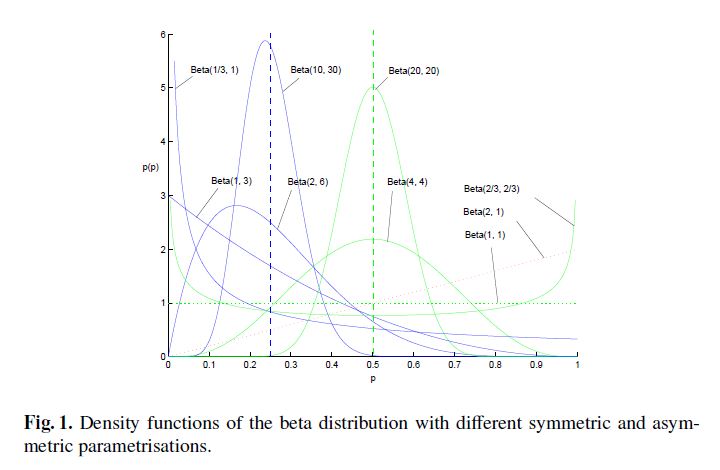
所以根据先验概率的要求，我们要求$p(p|\alpha, \beta)$,即：

$$p(p|\alpha,\beta) = {1 \over B(\alpha,\beta)}p^{\alpha-1}(1-p)^{\beta-1}$$
$$B(\alpha,\beta) = {{\Gamma(\alpha)\Gamma(\beta)}\over \Gamma(\alpha+\beta)}$$
根据图中的概率分布，我们假设这个硬币是均匀的，这里取 ${\alpha=\beta=4}$,通过这个假设来给我们最大似然估计求出的结果进行修正。
$$\hat \theta_{map} =ln((\prod_{i=1}^{10} p^{x_i}(1-p)^{(1-x_i)})\times {1 \over B(4,4)}p^{3}(1-p)^{3})$$
$${d\hat \theta_{map} \over dp} = {7 \over p}-{3 \over 1-p} + {3 \over p}-{3 \over 1-p} =0$$
$$p=0.5$$
这里比较凑巧， $p=0.5$，与我们的假设是比较相似的，准确度相比较最大似然估计似乎有一定提高。

参考

http://blog.csdn.net/yangliuy/article/details/8296481
http://www.cnblogs.com/liliu/archive/2010/11/24/1886110.html