250
Problem Statement | |||||||||||||
| The idols Ami and Mami like playing games. Today they bought a new game. At the beginning of the game a single slime appears on the screen. You are given an intS: the size of the slime. The game consists of K turns. In each turn of the game the player must choose a single slime and cut it into two smaller parts. More precisely, suppose that the player chose a slime of size z. When cutting this slime, the player must choose two positive integers x and y such that x+y = z. The player will then cut the slime into two smaller slimes. The sizes of those smaller slimes will be x and y, respectively. Note that the player must always choose a slime of size 2 or more, as it is not possible to cut a slime of size 1. The player gets a reward for making each cut: whenever you cut a slime of size x+y into slimes of sizes x and y, the player is awarded x*y mascots. Ami and Mami have just started a new game. You are given two ints S andM. Calculate and return the smallest possible K (the number of turns in the game) such that Ami and Mami can get at leastM mascots in the game. If there exists no such K, return -1 instead. | |||||||||||||
Definition | |||||||||||||
| |||||||||||||
Limits | |||||||||||||
| |||||||||||||
Constraints | |||||||||||||
| - | S will be between 2 and 1000, inclusive. | ||||||||||||
| - | M will be between 1 and 10^9, inclusive. | ||||||||||||
Examples | |||||||||||||
| 0) | |||||||||||||
| |||||||||||||
| 1) | |||||||||||||
| |||||||||||||
| 2) | |||||||||||||
| |||||||||||||
| 3) | |||||||||||||
| |||||||||||||
貌似是非常恶心的一题,记忆中做过类似的,但还是坑了题意:
两个人做游戏,一开始在屏幕上有一段长度为S的粘液,每一回合必须选择一段粘液并将其分割为长度为整数的两段(X+Y=Z)且得到分数X*Y。如果粘液的长度为1则无法继续分割。问:给出一个K,求出最少需要多少回合可以使总分大于等于K分析:
其实绝大多数人的第一反应都是对各段不断中分,也就是用贪心的策略不断求当前最优解
然而这样并没有什么卵用,貌似正确的方法是枚举所需的回合数R,将S尽可能地均分成R份,至于怎么证明,呵呵了
#include <cstdio> #include <iostream> #include <string> #include<assert.h> #include <algorithm> #include <vector> #include <cstring> #include <queue> #include <set> typedef long long int ll; #define rp(i,b) for(int i=(0),__tzg_##i=(b);i<__tzg_##i;++i) #define rep(i,a,b) for(int i=(a),__tzg_##i=(b);i<__tzg_##i;++i) #define repd(i,a,b) for(int i=(a),__tzg_##i=(b);i<=__tzg_##i;++i) #define mst(a,b) memset(a,b,sizeof(a)) using namespace std; struct SubdividedSlimes { int needCut(int S, int M) { rep(i,2,S+1) { int a = S/(i), b = S%(i), s = S; int r = 0; rep(j, 0, i) { int d = a; if (j+b >= i) ++d; r += d*(s-d); s -= d; } if (r >= M) return i-1; } return -1; } };
500
Problem Statement | |||||||||||||
| Given are ints N and L. A complete graph is a graph in which each pair of vertices is connected by exactly one undirected edge. A graph is called beautiful if:
The minimum spanning tree (MST) of a beautiful graph is its subgraph with the following properties:
An MST is called a line if the degree of each of its vertices is at most 2. Hibiki likes MSTs. She also likes lines. For each beautiful graph G, let f(G) be the number of its MSTs that are lines. (Note that for some beautiful graphs it may be the case that f(G)=0.) Let X be the sum of the values f(G) over all beautiful graphs G. Please calculate X for her. As X can be very large, compute and return the value (X modulo 1,000,000,007). | |||||||||||||
Definition | |||||||||||||
| |||||||||||||
Limits | |||||||||||||
| |||||||||||||
Constraints | |||||||||||||
| - | N will be between 2 and 200, inclusive. | ||||||||||||
| - | L will be between 1 and 200, inclusive. | ||||||||||||
Examples | |||||||||||||
| 0) | |||||||||||||
| |||||||||||||
| 1) | |||||||||||||
| |||||||||||||
| 2) | |||||||||||||
| |||||||||||||
| 3) | |||||||||||||
| |||||||||||||
| 4) | |||||||||||||
| |||||||||||||
题意:
在一个完全图中存在N个顶点,和N*(N-1)/2条无向边。给定L,每条边上可赋值X(1<=X<=L)。如此,可构造L^(N*(N-1)/2)个完全图。已知N、L,求出在这些图中最小生成树(每个节点的度最多为2,即一条线)的个数。
分析:
求最小生成树一般有两种贪心算法Prim和Kruskal,我们借用Kruskal的思想得出最小生成树上边的最大值一定不大于其他边最小值。设该最小生成树为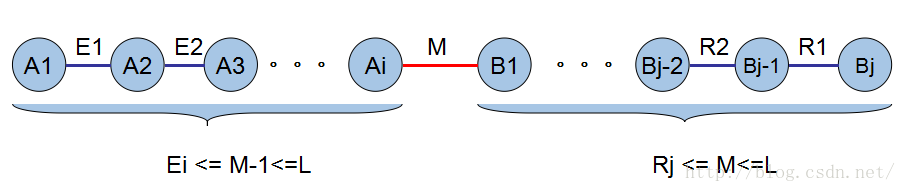
那么问题的关键在于如何计数,不考虑节点标号的情况下,设最小生成树有n个节点,边值最大为M的种数为dp(n,M)。那么最终的结果就是dp(N,L)*N!/2。为何要除以2?因为对于dp(n,M)中分为几类图:
第一类是自身具有轴对称性,例如边权完全相同第二类中,对于每种图均存在与之成轴对称关系的图,例如

在计算dp(n,M)的过程中,将点分成左右两部分,连接两部分的边(红色)表示从左开始第一次出现权为M的边,那么
dp(n,M) = dp(n, M-1) + sum(dp(i,M-1)*dp(n-i, M)*(i*(n-i)-1)^(L-M+1)) {1<=i<n}
#include <cstdio> #include <iostream> #include <string> #include <algorithm> #include <vector> #include <cstring> #include <queue> #include <set> #include <cmath> #include <map> #include <queue> #include <stack> #include <sstream> using namespace std; typedef long long ll; #define urp(i,a,b) for(int i=(a),__tzg_##i=(b); i>=__tzg_##i; --i) #define rp(i,b) for(int i=(0), __tzg_##i=(b);i<__tzg_##i;++i) #define rep(i,a,b) for(int i=(a), __tzg_##i=(b);i<__tzg_##i;++i) #define repd(i,a,b) for(int i=(a), __tzg_##i=(b);i<=__tzg_##i;++i) #define mst(a,b) memset(a,b,sizeof(a)) typedef pair<int,int> pii; #define px first #define py second const ll mod = 1000000007; const int MAXN = 220; const int MAXM = 15; const double eps = 1e-6; #define mp(a,b) make_pair(a,b) typedef vector<int> VI; typedef vector<double> VDB; typedef vector<ll> VL; typedef vector<pii> VPII; typedef vector<string> VS; typedef vector<VI> VVI; typedef vector<VL> VVL; struct LineMST { int count(int N, int L) { VVL dp(N+1, VL(L+1, 0)); VVL pow(L+1, VL(N*N+1, 1)); rep(i, 1, L+1) rep(j, 1, N*N+1) { pow[i][j] = pow[i][j-1] * i % mod; } dp[1] = VL(L+1, 1); rep(i, 2, N+1) { rep(j, 1, L+1) { dp[i][j] = dp[i][j-1]; rep(k, 1, i) { dp[i][j] = (dp[i][j] + dp[k][j-1]*dp[i-k][j]%mod*pow[L+1-j][k*(i-k)-1]) % mod; } } } ll res = dp[N][L]; rep(i, 3, N+1) res = res*i%mod; return res; } };
























 1442
1442











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








