一、题目得分:
T1下棋(chess) 70
T2汪洋(BigWater) 15
T3删数(delnum) 0
T4平分糖果(candy) 30
二、赛中情况:
因为电脑坏了,所以我晚了10分钟才开始做题。第一题用了10分钟就做完了,本来只是一个简简单单的结构体排序,能得满分,但因为longlong得了70分。不开longlong见祖宗;第二题用了dfs,本应该用前缀和+模拟(关键是我没学前缀和啊!!!),应该在求和时用前缀和优化,前缀和O(1),求和O(n);第三题是一道思维题(没有算法,只能想出来,换个思维想,一般CSP-J第二题是思维题,跟脑筋急转弯类似),想不出来只能暴力,所以先写暴力在想;
三、题目解析:
下棋(chess)
1 问题描述
Meowowco 最近沉迷下棋。
众所周知,棋盘上一局有 nn 个玩家一起游戏。
我们的棋子称为”英雄”,英雄分为1、2、3星。1 个 3 星英雄可以由 3 个 2 星英雄合成,1 个 2 星英雄可以由 3 个 1 星英雄合成。
现在给出每名玩家的英雄阵容,我们定义阵容强度为18x+3y+z,其中 x 为 3 星英雄个数,y 为两星英雄个数,zz 为一星英雄个数,其中可以用低星英雄合成高星英雄后再计算阵容强度。
根据玩家的阵容强度,将玩家序号进行排序,并按阵容强度从大到小的顺序输出玩家的序号(若阵容强度相同,则把玩家序号(第ii个输入的玩家序号为ii)小的排在前面)。
2 输入格式
第一行输入一个整数 nn (1≤n≤100000),表示有n名玩家参加游戏。
接下来nn行,每行包含三个整数,代表玩家 i 的一星、二星、三星英雄的数量。
3 输出格式
将玩家序号进行排序,并按阵容强度顺序输出玩家的序号(若阵容强度相同,则按玩家序号排序)。
4 输入样例1
9 2 3 1 1 3 3 0 0 4 1 4 3 4 1 4 1 4 1 0 1 4 0 1 4 2 3 25 输出样例1
5 4 7 8 2 3 9 6 16 输入样例2
2 1 2 0 1 2 27 输出样例2
2 18 数据描述
保证所有数据点均满足 1≤n≤105,0≤x,y,z≤109。
#include<bits/stdc++.h>
using namespace std;
struct A{
long long d,b,c,id,sum;//long long!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
}a[100010];
long long n;
bool cmp(A x,A y){
if(x1!=y1)return x1>y1;
else return x.i1<y.i1;
}
int main(){
scanf("%lld",&n);
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld",&a[i].d,&a[i].b,&a[i].c);
a[i].id=i;
a[i].b+=a[i].d/3;
a[i].d%=3;
a[i].c+=a[i].b/3;
a[i].b%=3;
a[i].sum = x.d+x.b*3+x.c*18;
}
sort(a+1,a+n+1,cmp);
for(int i=1;i<=n;i++)printf("%lld ",a[i].id);
return 0;
}汪洋(BigWater)
1 问题描述
Meowowco 连夜坐飞机去参加上海国家会展中心的 BilibiliWorld 2023,可是到现场时,已经是一片汪洋。
就算是这样,Meowowco 也不算白来一趟,因为场馆里还有许多可爱的 coser,她可以和这些 coser 一起合影,然后发说说羡慕她那可怜的队友。
场馆可以看成一张由 n×nn×n 个格子构成的矩阵。场馆内的格子可能被水淹没,Meowowco 趟水走过去可能会影响心情,因此这些格子上的值为 负数。但是另外的一些格子上站着可爱的 coser,如果 Meowowco 可以与那些 coser 合影,那么她就会变得开心,因此这些格子的值为 正数。
Meowowco 最开始的心情为 100 点,她在逛 BW 的过程中:
如果走到值为正数的格子,说明可以和可爱的 coser 拍照,因此会增加心情。
如果走到值为负数的格子,说明 Meowowco 需要趟水,因此心情值会下降。
Meowowco 从 (1,1) 点向右出发,即朝 (1,2) 点出发,她每次移动只能移动到 一个相邻的格子,并且她需要按照下面的路线逛一圈:
沿着上一步的方向继续移动
进行顺时针 90 度转向,(注意不可以在同一个格子内连续转向)
不再逛那些逛过的格子(除了起点)
其中转向指的是:如果上一步向右走,那么转向之后则为向下走;如果上一步向左走,那么转向之后则为向上走……
那么逛完 BW 之后,肯定是要从 (1,1) 点离开然后回家的,那么问题来了,Meowowco 离开时心情值最大是多少。
2 输入格式
从文件
BigWater.in中读取数据。第一行输入一个整数 n,表示地图的大小。
第二到 N+1 行,每行包含 n 个整数 a[i][j],表示每个格子的值。
保证 (1,1) 点为 0。
3 输出格式
输出到文件
BigWater.out中。输出一个整数,表示 Meowowco 最大的心情值。
4 输入样例1
5 0 -3 8 -2 3 3 -1 -3 -10 -6 9 -9 -6 10 -7 -2 -4 -9 6 -10 -1 8 -7 10 -55 输出样例1
1296 数据描述
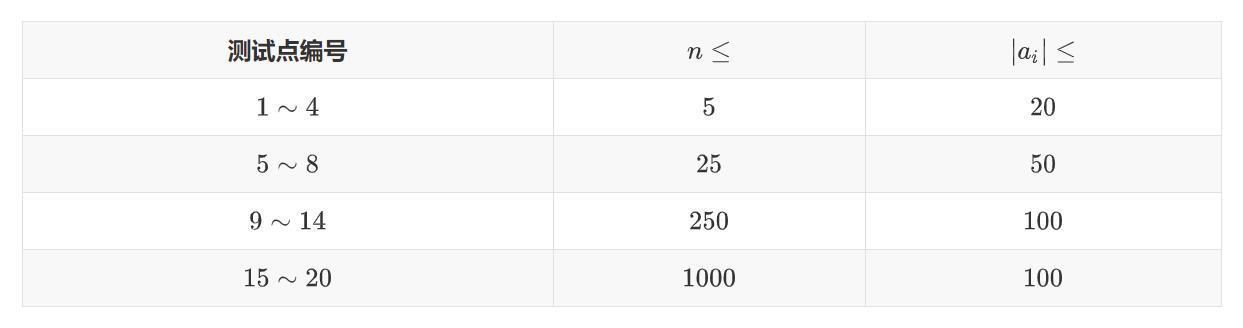
保证所有数据点均满足 1≤n≤1031≤n≤103,∣ai∣≤100∣ai∣≤100。
我们可以发现 Meowowco走的路程是一个矩阵,所以我们遍历右下角的数字将它上、下、左、右的边相加,所以公式是:b[i][j]-b[i-1][j-1]+b[i-1][1]+b[1][j-1]
#include<bits/stdc++.h>
using namespace std;
long long n,a[1010][1010],b[1010][1010]={0},ma=-2147483648;
int main(){
scanf("%lld",&n);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
scanf("%lld",&a[i][j]);
b[i][j]=b[i-1][j]+b[i][j-1]-b[i-1][j-1]+a[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
ma=max(ma,b[i][j]-b[i-1][j-1]+b[i-1][1]+b[1][j-1]);//减是因为四个角会重复
}
}
printf("%lld",ma+100);//100为一开始小Meowowco的心情
return 0;
}前两题简单,就不细讲了。
删数(delnum)
上一题下一题
题目描述
我的提交
题解
时间限制:1秒 内存限制:256M
3.1 问题描述
有一个集合,初始状态里面有数字 1、2、3、4、5、……、1145141919810,你可以理解为很多正整数。
现在给你一个长度为 nn 数组 a(1≤ai≤109)a(1≤ai≤109),每次操作将当前集合中第 a1a1 小、第 a2a2 小、……、第 anan 小的数同时移除。
现在有 qq 次询问,每次询问包含一个整数 xx,查询从初始状态到删除 xx 需要操作多少次。若无法删除,输出
0。3.2 输入格式
第一行包含两个正整数 n(1≤n≤105),表示数组大小。
接下来一行包含 n 个正整数 a1,a2,……,an,含义如题目描述所述。
接下来一行包含一个正整数 qq,表示查询次数。
接下来 qq 行,每行包含一个正整数 xx。
数据保证 a1<a2<.....<an≤109
3.3 输出格式
对于每次询问,输出占一行,包含一个整数,表示删除 xx 需要操作多少次。若无法删除,输出
0。3.4 输入样例
51 2 3 4 511003.5 输出样例
203.6 输入样例
51 3 9 14 20511451419198102333.7 输出样例
27107388159453.8 数据描述
保证所有数据点均满足 1≤n≤1051≤n≤105,1≤ai≤1091≤ai≤109,1≤q≤501≤q≤50,1≤x≤1091≤x≤109。
假设样例为:
2
1 101
1
100
那么受到这个删数影响的100只有1一个数,可以多试几个样例,发现都是这样,所以x = x-i,从而推导出
for(int i = n;i >= 1;i--){//要倒序
if(x > arr[i]){
ans += (x - arr[i]) / i;//求答案
x = arr[i] + (x - arr[i]) % i;//求x-i
if(x > arr[i]){
ans ++;
x -= i;
}
}
}代码如下:
#include<iostream>
using namespace std;
int arr[1000010];
int main(){
int n,q;
cin >> n;
for(int i = 1;i <= n;i++){
cin >> arr[i];
}
cin >> q;
while(q--){
int x;
cin >> x;
int ans = 0,f = 0;
for(int i = n;i >= 1;i--){
if(x > arr[i]){
ans += (x - arr[i]) / i;
x = arr[i] + (x - arr[i]) % i;
if(x > arr[i]){
ans ++;
x -= i;
}
}
if(x == arr[i]){
cout << ans + 1 << endl;
f = 1;
break;
}
}
if(f == 0){
cout << "0\n";
}
}
return 0;
}
分糖果(candy)
1 问题描述
小可的妈妈给了小可很多的糖果,已经糖果都有美味程度,美味程度用1~6的整数表示。
有一天达达来小可家做客,小可要把糖果分给达达,现在已知了美味程度为 i 的糖果有 a[i] 个,请问小可能不能把糖果平分成美味程度之和相同的两部分。
2 输入格式
多组输入,每行输入6个数字,表示美味程度为 i 的糖果有 a[i] 个。
以输入一行6个0作为终止条件。
3 输出格式
对于每组输入,第一行输出为:
Collection #k:,k为第几组输入。第二行输出为:如果可以平均分,则输出
Can be divided.,否则输出Can't be divided.。4 输入样例
1 0 1 2 0 01 0 0 0 1 10 0 0 0 0 05 输出样例
Collection #1:Can't be divided.Collection #2:Can be divided.6 数据描述
20%的数据:糖果总数不超过100
100%的数据:糖果总数不超过 20000
“正确”代码:(被hack家族hack掉了)
#include<iostream>
using namespace std;
int arr[10];
int main(){
int cnt = 0,e,l,r;
while(1){
cnt ++;
e = l = r = 0;
int sum = 0;
for(int i = 1;i <= 6;i++){
cin >> arr[i];
sum = arr[i] * i;
if(arr[i] == 0) e++;
}
if(e == 6) return 0;
for(int i = 6; i >= 1;i--){//l少加在l上,l多加在r上
while(arr[i] > 0){
if(l > r){
r += i;
}else{
l += i;
}
arr[i] --;
}
}
printf("Collection #%d:\n",cnt);
if(l == r){
printf("Can be divided.\n\n");
}else{
printf("Can't be divided.\n\n");
}
}
return 0;
} 正确代码:(被hack3hack掉了)
DP 多重背包
#include<iostream>
using namespace std;
int dp[10][200010];
int a[10];
int main(){
int cnt = 0,e,l,r;
while(1){
int m = 0;
for(int i = 1;i <= 6;i++){
cin >> a[i];
m += a[i] * i;
}
if(!m) break;
dp[0][0] = 1;
for(int i = 1;i <= 6;i++){//第i件物品
for(int k = 0;k <= a[i];k++){//可用次数
for(int j = k * i;j <= m / 2 + 1;j++){//和为j
dp[i][j] = dp[i][j] | dp[i-1][j - k * i];
}
}
}
printf("Collection #%d:\n",++cnt);
if(m % 2 == 0 && dp[6][m / 2 + 1] == 1){
printf("Can be divided.\n\n");
}else{
printf("Can't be divided.\n\n");
}
}
return 0;
} hack : 0 0 5 1 5 0























 5605
5605

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








