本文地址:http://blog.csdn.net/spch2008/article/details/38942175
描述
之前写过一篇最长公共子序列, 今天来补上最长公共子串. 子序列: 不要求字符串联系,只要顺序一致即可. 子串: 要求字符串必须连续.
A:acaccbabb
B:acbac
最长子序列: acac (要求顺序不变即可)
最长子串:cba (要求必须连续)
其实,最长子串问题完全可以由最长子序列问题演变而来。下面分析一下最长公共子序列的递推公式:
当xi 与 yj 不相等的时候,我们要继承前一个最长公共子序列的长度。而对于子串来说,不相等,意味着这次比较结束,
直接赋0即可c[i][j] = 0。
int LCS_IMP(char *X, char *Y, int lenX, int lenY, int **c)
{
//初始化
for(int i = 0; i < lenX + 1; i++)
{
c[i][0] = 0;
}
for(int j = 0; j < lenY + 1; j++)
{
c[0][j] = 0;
}
int maxlen = 0;
for(int i = 1; i < lenX + 1; i++)
{
for(int j = 1; j < lenY + 1; j++)
{
if(X[i-1] == Y[j-1])
{
c[i][j] = c[i-1][j-1] + 1;
}
else
{
c[i][j] = 0;
if ( c[i-1][j-1] > maxlen)
maxlen = c[i-1][j-1];
}
}
}
return maxlen;
}
int LCS(char *X, char *Y, int lenX, int lenY)
{
//开辟数组空间
int **c = new int*[lenX + 1];
for(int i = 0; i < lenX + 1; i++)
c[i] = new int[lenY + 1];
int max_len = LCS_IMP(X, Y, lenX, lenY, c);
//释放数组空间
for(int i = 0; i < lenX + 1; i++)
{
delete [] c[i];
}
delete [] c;
return max_len;
}优化
注意到最长子串与子序列的不同,即子串不需要记录c[i][j-1], c[i-1][j]的值,这就有了优化的空间。在最长子串中,
唯一的推导公式为 c[i][j] = c[i-1][j-1] + 1, 也就是说,下一行,仅仅依赖上一行的记录值。
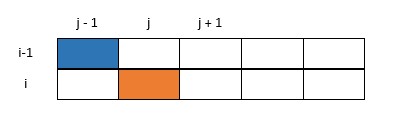
c[i][j] = c[i-1][j-1] + 1; 如下图所示。当第二行值计算出来后,第一行值不再需要,可以丢弃。
此时,将第一行,即i-1当做第j+1 行使用,依赖第i行获取依赖值。c[i+1][j+1] = c[i][j] + 1;
问题:
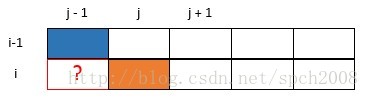
1. 按照这个推导规则,仅仅使用两行即可,不停的在这两行间做变换,来模拟第i行,第i+1行等。
2. 下一行的第一个元素无法通过推导的出来。即下图中 ? 处, 这个需要单独处理。
int LCS(char *X, char *Y, int lenX, int lenY)
{
//开辟数组空间
int **c = new int*[2];
for(int i = 0; i < 2; i++)
c[i] = new int[lenY];
//初始化
for(int i = 0; i < 2; i++)
for (int j = 0; j < lenY; j++)
c[i][j] = 0;
int maxlen = 0;
int begin = -1;
for(int i = 0; i < lenX; i++)
{
// 上下两行进行切换, 解决问题1
int curr = ((i & 1) == 0);
int prev = ((i & 1) == 1);
// 首位赋值, 解决问题2
if(X[i] == Y[0])
c[curr][0] = 1;
else
c[curr][0] = 0;
for(int j = 0; j < lenY; j++)
{
if(X[i] == Y[j])
{
c[curr][j] = c[prev][j-1] + 1;
}
else
{
c[curr][j] = 0;
if (c[prev][j-1] > maxlen)
{
maxlen = c[prev][j-1];
begin = j - maxlen;
}
}
}
}
//释放数组空间
for(int i = 0; i < 2; i++)
{
delete [] c[i];
}
delete [] c;
//打印子串
if (begin != -1)
{
for (int j = begin; j <= maxlen; j++)
cout << Y[j];
cout << endl;
}
return maxlen;
}









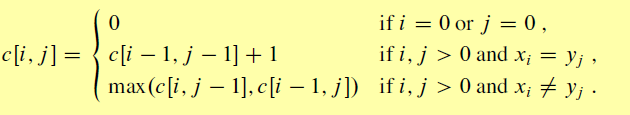















 328
328

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








