【排序算法】03：堆与堆排序

本文为王争《数据结构与算法之美》笔记。

一、堆

1.定义

堆是一个完全二叉树，且堆中每一个节点的值都满足：大于等于/小于等于其左右节点的值。“大于等于”：大顶堆。“小于等于”：小顶堆。

2.实现

堆是一个完全二叉树，故通常用数组来存储。
我在这篇文章中，自己实现了一个优先级队列MinPQ来解决LeetCode 23.合并K个升序链表。而优先级队列的底层就是小顶堆。
MinPQ的实现模仿了JDK的PriorityQueue，使用了Java的泛型机制。MinPQ的通用性就体现在，它的构造器参数中有一个Comparator<K> comparator，而Comparator<T>是一个典型的函数式接口（见这篇文章）。所以，在构造一个MinPQ时，你可以传入一个Lambda表达式来代替参数列表中的Comparator<K> comparator。你可以随意定制Lambda表达式，来改变more()函数的比较机制。比如，在本题的代码中，Lambda表达式是这样的：(node1, node2)->(node1.val - node2.val)。
另外，MinPQ没有写grow()方法，不能扩容。
swim、sink、insert、delMin这四个方法是核心，代码实现来自公众号labuladong的文章《图文详解二叉堆，实现优先级队列》。
另外，如果堆从queue[0]就开始存储，那么left、right、parent方法需要改成：

private int parent(int k){
    return (k-1) / 2;
}
private int left(int k){
    return 2*k + 1;
}
private int right(int k){
    return 2*k + 2;
}

下面是MinPQ的完整代码：

//小顶堆：完全二叉树，且每个节点的值都小于等于它左右子节点的值
class MinPQ<K> {
    //存储元素的数组
    private K[] queue;
    //当前堆中的元素个数
    private int n;
    //堆的最大容量
    private int capacity;
    //Comparator:典型函数式接口
    private Comparator<K> comparator;
    //构造器
    public MinPQ(int cap, Comparator<K> comparator){
        //索引0不用，所以是cap+1
        this.queue = (K[]) new Object[cap + 1];
        this.n = 0;
        this.capacity = cap;
        this.comparator = comparator;
    }
    //返回堆中最小的元素
    public K min(){
        return queue[1];
    }
    public boolean isEmpty(){
        return n == 0;
    }
    public void insert(K e){
        //如果堆满了，则添加不进去
        if(n >= capacity) return;
        n++;
        queue[n] = e;
        swim(n);
    }
    public K delMin(){
        //如果堆空了，则删除不了，返回null
        if(n == 0) return null;
        //把最小元素换到最后
        exch(1,n);
        //存下原最小元素的值，然后删除
        K min = queue[n];
        queue[n] = null;
        n--;
        sink(1);
        return min;
    }
    private void swim(int k){
        while(k > 1 && more(parent(k),k)){
            exch(k, parent(k));
            k = parent(k);
        }
    }
    private void sink(int k){
        while(left(k) <= n){
            int smaller = left(k);
            if(right(k) <= n && more(left(k),right(k)))
                smaller = right(k);
            if(more(smaller,k))
                break;
            exch(k, smaller);
            k = smaller;
        }
    }
    //交换pq数组中的两个元素
    private void exch(int i, int j){
        K temp = queue[i];
        queue[i] = queue[j];
        queue[j] = temp;
    }
    //判断pq[i]是否大于pq[j]
    private boolean more(int i, int j){
        //不能直接用">"
        return comparator.compare(queue[i],queue[j]) > 0;
    }
    //计算父节点和左右子节点的索引值
    private int parent(int k){
        return k / 2;
    }
    private int left(int k){
        return 2*k;
    }
    private int right(int k){
        return 2*k + 1;
    }
}

二、堆排序

为方便解题，堆排序部分的堆一律从数组的0索引开始存储。

1.思路

（1）先堆化

对于一个数组，先要将其“堆化”，让这个数组成为一个大顶堆（默认：升序为有序）。
如何将数组原地堆化呢？

堆化思路一：插入法

假设最开始堆中只有一个数据，就是nums[0]，我们将nums[1]插入这个大小为1的堆中。然后，我们再将nums[2]插入到这个大小为2的堆中……以此类推，最后我们将nums[n-1]插入到这个大小为n-1的堆中。这样，一个堆就原地建成了。
根据堆的实现，插入操作的底层是：与父结点比较然后上浮。二叉树第i层有2^(i-1)个节点，每个节点最多上浮i-1层。我们对第2层到第[logn]+1层的所有结点都进行了插入操作。
所以，插入法在最坏的情况下，其比较与交换的次数是：
【图片来自这篇知乎文章，作者：乔胤博】

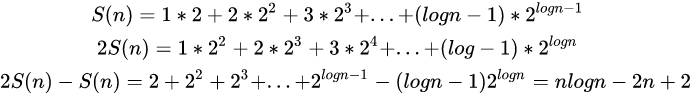
可见插入法建堆的最坏时间复杂度为O(n*logn)级别。
那么，有没有更好的方法呢？

堆化思路二：下沉法

插入法的实际操作，就是对每个非根节点进行上浮。而第二个思路，就是对每个非叶子节点进行下沉。由于nums[n/2]到nums[n-1]都是叶子节点，没有下沉的必要，所以我们把节点nums[n-2]~nums[0]都下沉就好，这里就体现了下沉法比插入法更好的地方：需要处理的节点更少。
【PS：根据从0索引开始存储的完全二叉树的性质，节点nums[k]的父节点是nums[(k-1)/2]。代入n-1可得，最后一个节点nums[n-1]的父节点是nums[n/2 -1]。也就是说父节点nums[n/2 -1]是最后一个拥有子节点的节点，因此nums[n/2]到nums[n-1]都是叶子节点】
最坏情况下，每个非叶子节点都要下沉到底部。设堆的高度为h，h≈logn。下沉h-1层的节点，最多下沉一层，以此类推。
非叶子节点在1~h-1层分布。在二叉树不是满二叉树时，h-1层也有叶子节点，这里我们认为h-1层都是非叶子节点，叶子节点都在h层。
我们对每个非叶子节点的最大下沉高度求和，就得到：
（下面几张图都来自王争《数据结构与算法之美》）


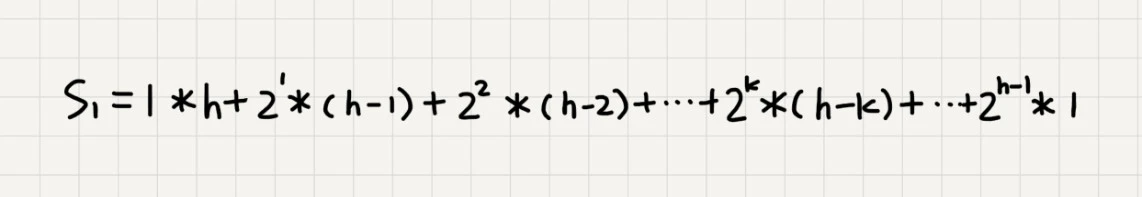
所以交换次数最多为：

又因为h≈log2n，代入可得下沉法建堆的最坏时间复杂度为O(n)。
下沉法比起插入法，需要处理的节点更少，由此我们可以粗略地认为下沉法效率更高。而经过了时间复杂度的计算，我们得知下沉法的耗时确实更少。因此，我们通常使用下沉法来进行堆化。
下沉法代码实现：

void heapify(int[] nums){
    int n = nums.length;
    for(int i = n/2-1; i>=0; i--){
        sink(nums,i,n);
    }
}
void sink(int[] nums, int k, int r){
    while(left(k) < r){
        int bigger = left(k);
        if( right(k) < r && nums[left(k)] < nums[right(k)] )
            bigger = right(k);
        if( nums[bigger] <= nums[k] )
            break;
        exch(nums, k, bigger);
        k = bigger;
    }
}

（2）再调整

堆化之后，数组就成了大顶堆，nums[0]是最大的，将它和第n个值（最后一个）交换，最大值就到了该到的位置。
然后将前n-1个元素看作一个堆，将交换后的nums[0]进行下沉，就得到了新的堆。此时的nums[0]是第二大的，和第n-1个值交换，第二大的值就到了该到的位置。
一直重复这个过程，直到堆中只剩下一个元素，说明已经调整完成。
下沉操作决定了调整的耗时数量级。
【图片还是来自这篇知乎文章，作者：乔胤博】

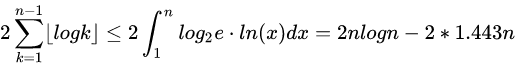
可知调整过程的时间复杂度为O(n*logn)。

2.代码

class Solution {
    public int[] sortArray(int[] nums) {
        heapify(nums);
        adjust(nums);
        return nums;
    }
    void heapify(int[] nums){
        int n = nums.length;
        for(int i = n/2-1; i>=0; i--){
            sink(nums,i,n);
        }
    }
    void adjust(int[] nums){
        int n = nums.length;
        for(int i = n-1; i>=1; i--){
            exch(nums,0,i);
            sink(nums,0,i);
        }
    }
    //r是现在堆的大小，将它添加到形参是为了堆化后的调整
    void sink(int[] nums, int k, int r){
        while(left(k) < r){
            int bigger = left(k);
            if( right(k) < r && nums[left(k)] < nums[right(k)] )
                bigger = right(k);
            if( nums[bigger] <= nums[k] )
                break;
            exch(nums, k, bigger);
            k = bigger;
        }
    }
    void exch(int[] nums, int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
    int parent(int k){
        return (k-1) / 2;
    }
    int left(int k){
        return 2*k + 1;
    }
    int right(int k){
        return 2*k + 2;
    }
}

3.性能分析

时间复杂度： 先用下沉法原地建堆，时间复杂度为O(n)；再排序，时间复杂度为O(nlogn)，于是总体时间复杂度为O(nlogn)。
空间复杂度： 整个过程只用了个别存储空间，所以空间复杂度为O(1)，是原地排序算法。
稳定性： 堆排序不稳定。因为在堆顶元素与最后元素交换的过程中，很可能会改变原有相同值元素的顺序。

4.在实际开发中，为什么快速排序要比堆排序性能好？

（1）堆排序数据访问方式没有快排友好

堆排序的两大操作，堆化和调整，都大量使用了下沉sink()方法，而sink()方法又大量使用left()、right()、parent()方法进行数组的跳跃式访问。而快速排序中，大量使用的是分区partition()方法，对数组进行的是局部顺序访问。
访问数组方式的不同对效率有什么影响呢？
我们知道，数组使用连续内存空间。因此在读取数组数据时，可以利用CPU 的缓存，预读一小块局部的数组数据，提高访问效率。而如果进行的是跳跃式访问，CPU 缓存的命中率就会降低，只能频繁访问内存，使得效率降低。

（2）堆排序的数据交换次数可能会多于快排

基于比较的排序算法有两个原子操作：比较和交换（或移动）。快排的数据交换次数不会超过逆序度（这一点还解释不清）。然而堆排序在一开始的堆化过程中就会打乱原有顺序，导致最后的数据交换次数可能会超过原始逆序度。举一个极端情况：数组一开始是有序的，经过堆化之后变得无序，逆序度反而变高。