计算机自称原理——基本运算

计算机系统的运行靠的是CPU中计算单元高效的运算，这篇文章旨在讲述ALU（算术逻辑单元）的各种运算方法与运算部件

一.C语言中涉及的运算

C中涉及的运算一共有这三种：按位运算，逻辑运算，移位运算，以及扩展与截断。

按位运算：按位运算是直接对二进制位（bit）进行操作的计算方式

逻辑运算：逻辑运算用于布尔值（true/false）的条件判断，控制程序流程。

这两个基本上就是与或非，考的不多

移位运算：移位运算分算术移位以及逻辑移位

算数移位：关注有符号数值处理，移位过程中符号位保持不变。左移时，最高位的符号位被复制到移出位置；右移时，正数右侧填充0，负数右侧填充符号位的值。

逻辑移位：用于无符号数值处理，移位过程中不考虑符号位。左移和右移时，空出的位置均填充0。

接下来我们看一道例题

例 已知32位寄存器R1中存放的变量x的机器数为80 00 00 04H，请回答下列问题。

(1) 当x是unsigned int类型时，x的值是多少？x/2的值是多少？x/2存放在R1中的机器数是什么？2x的值是多少？2x存放在R1中的机器数是什么？

(2) 当x是signed int类型时，x的值是多少？x/2的值是多少？x/2存放在R1中的机器数是什么？2x的值是多少？2x存放在R1中的机器数是什么？

解：(1)当x是unsigned int类型时，x是无符号数，机器数80 00 00 04H的真值是 +100000000000000000000100B=231+22

对于x/2的情况：

一方面，根据x的真值得x/2的值为 (231+22)/2=230+2 ；另一方面，x/2的机器数通过对x逻辑右移一位得到，因此，x/2存放在R1中的机器数是

0100 0000 0000 0000 0000 0010=40 00 02H

由上述机器数得x/2的真值为2^30+2。因此，根据x的真值求出的x/2的值与对x的机器数逻辑右移得到的x/2的值是一样的。

对于2x的情况：

一方面，根据x的真值得2x的值为 (231+22)×2=232+23 ；另一方面，2x的机器数通过对x逻辑左移一位得到，因此，2x存放在R1中的机器数是

0000 0000 0000 0000 0000 1000=00 00 08H

由上述机器数得2x的真值为2^3=8。显然，2^32+2^3不等于8，说明结果溢出。

以下是MIPS指令中所有涉及的运算（共有21 个算术指令 （+， -， *， /， %）8 个逻辑指令 （&， |， ~））

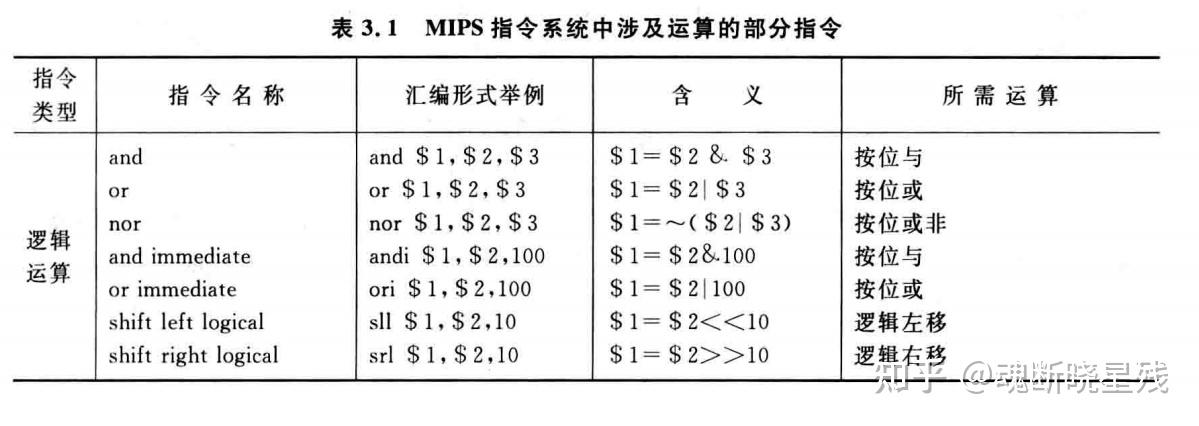
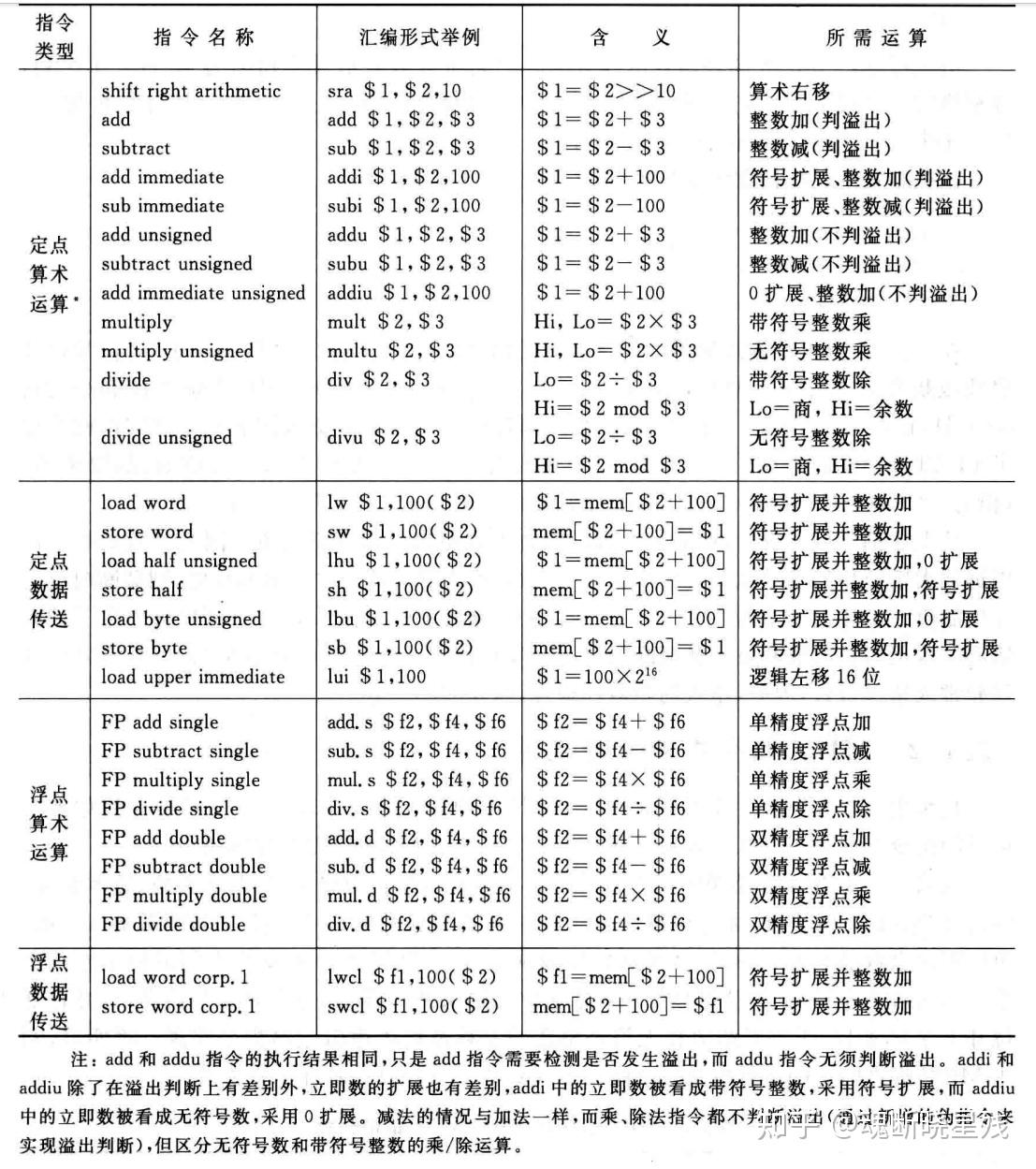
二：基本运算部件

2.1.加法器

2.1.1 串行进位加法器

实现原理是两个加数与进位相加，表达式如下

Fi=Xi⊕Yi⊕Ci−1Ci=XiCi−1+YiCi−1+XiYi

逻辑电路如下

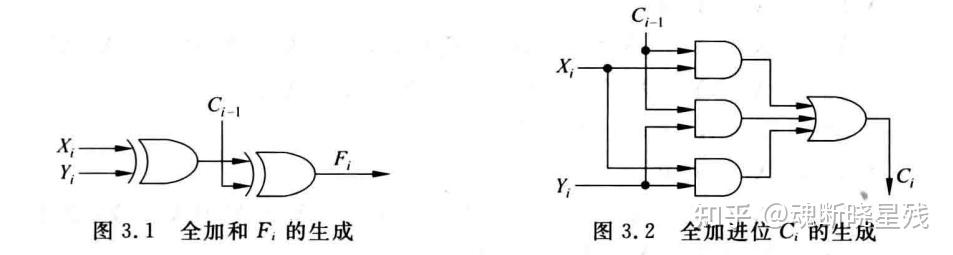
直观理解就是加数相加，进位传送，就像波纹一样推到尽头，以下是加法器的表现形式

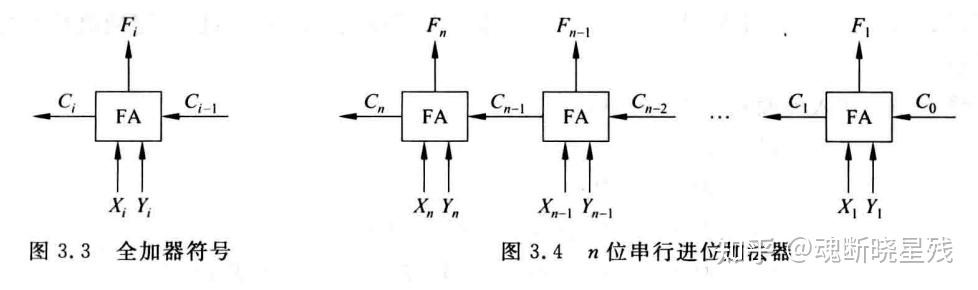
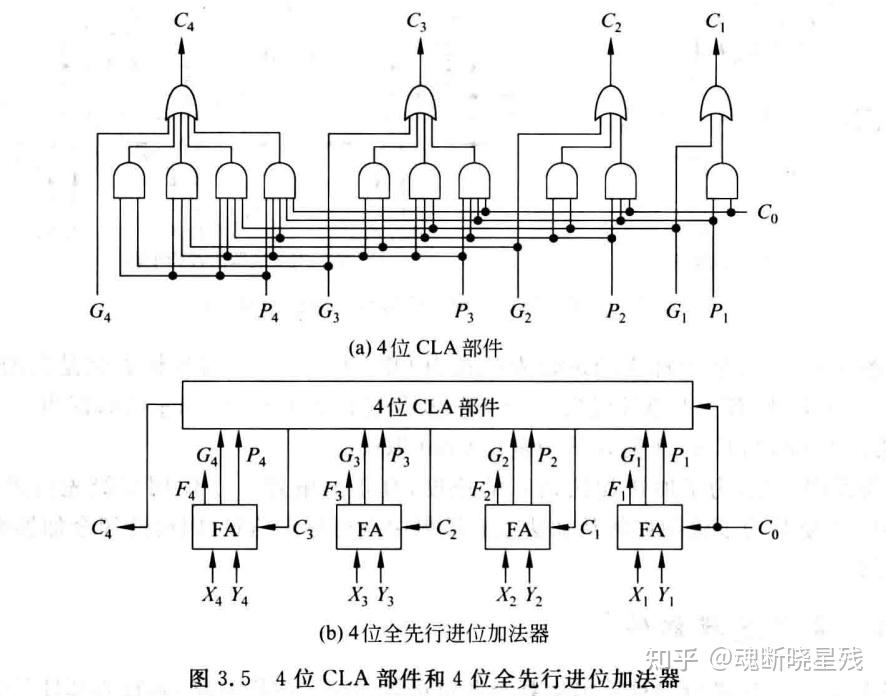
2.1.2并行进位加法器

计算机中加法运算是频繁的，同时进位运算又是低效的，为了效率推出了并行进位加法器

C=X1Y1+(X1+Y1)C0C2=X2Y2+(X2+Y2)C1=X2Y2+(X2+Y2)X1Y1+(X2+Y2)(X1+Y1)C0C3=X3Y3+(X3+Y3)C2=X3Y3+(X3+Y3)[=X3Y3+(X3+Y3)X2Y2+(X3+Y3)(X2+Y2)X1Y1+(X3+Y3)(X2+Y2)(X1+Y1)C0C4=X4Y4+(X4+Y4)C3=X4Y4+(X4+Y4)[X+(X3+Y3)(X2+Y2)(X1+Y1)C0]=X4Y4+(X4+Y4)X3Y3+(X4+Y4)(X3+Y3)X2Y2+(X4+Y4)(X3+Y3)(X2+Y2)X1Y1+(X4+Y4)(X3+Y3)(X2+Y2)(X1+Y1)C0

换元后经过整理得

C1=G1+P1C0C2=G2+P2G1+P2P1C0C3=G3+P3G2+P3P2G1+P3P2P1C0C4=G4+P4G3+P4P3G2+P4P3P2G1+P4P3P2P1C0

其中 ，Pi=Xi+Yi，Gi=XiYi

以下是逻辑电路与示意图

2.1.3 带标志加法器

以下是带标志加法器的结构

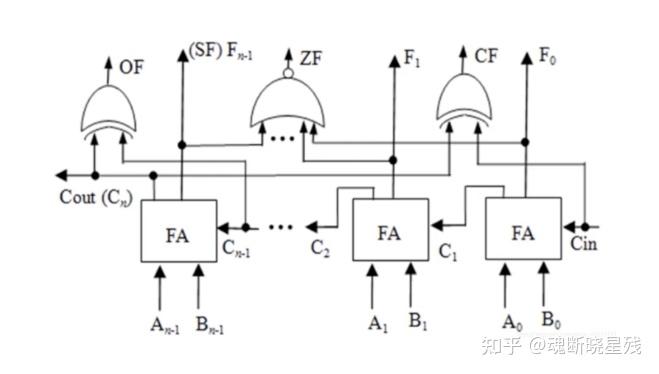
OF(溢出标志):指示带符号数运算是否溢出，计算公式为 OF=Cn⊕Cn−1 (最高位进位与次高位进位异或)。

SF (符号标志):取运算结果的最高位， SF=Fn−1 ,表示带符号数的正负。

ZF(零标志):当结果所有位为0时置1，ZF=¬(F0∨F1∨...vFn-1)。

CF (进位/借位标志):用于无符号数溢出判断， CF=Cout⊕Cin (加法时 Cin=0,减法时 Cin=1)。

例：

OF (溢出标志): 带符号数加减时，若两个正数相加结果为负(或两个负数相加结果为正),则 OF=1 。例

如，4位补码中 0111(7) + 01111(7) =11110(-2)会触发溢出。

CF (进位/借位标志): 无符号数运算时，若最高位产生进位(加法)或借位(减法),则 CF=1 。例如，

11111(15)+0001(1)=0000(0)且CF=1。

2.1.4算术逻辑部件

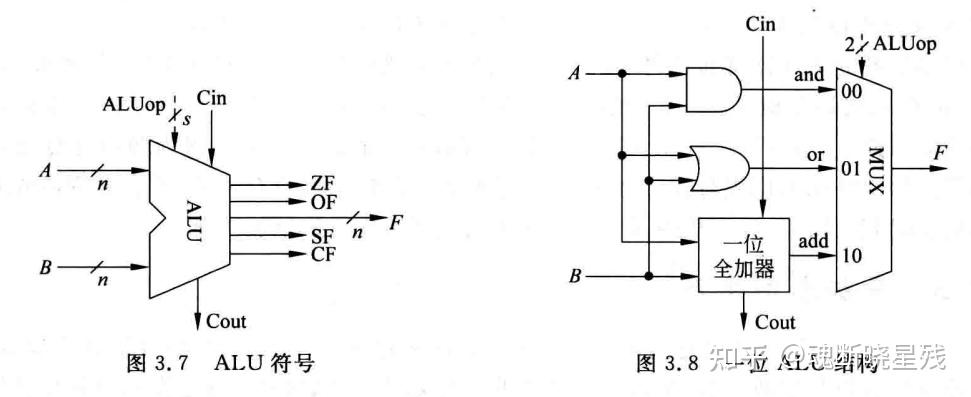
运算的操作基本上都集成在算术逻辑单元上

然后我们解决几道真题

【2009统考真题】一个C语言程序在一台32位机器上运行。程序中定义了三个变量x,y,z，其中x和z为int型，y为short型。当x=127,y=-9时，执行赋值语句z=x+y后，x,y,z的值分别是( )。

A. x = 0000007FH, y = FFF9H, z = 00000076H

B. x = 0000007FH, y = FFF9H, z = FFFF0076H

C. x = 0000007FH, y = FFF7H, z = FFFF0076H

D. x = 0000007FH, y = FFF7H, z = 00000076H

【2010统考真题】假定有四个整数用8位补码分别表示：r1=FEH,r2=F2H,r3=90H,r4=F8H，若将运算结果存放在一个8位寄存器中，则下列运算会发生溢出的是( )。

A. r1×r2

B. r2×r3

C. r1×r4

D. r2×r4

B显然超了

【2013统考真题】某字长为8位的计算机中，已知整型变量x,y的机器数分别为[x]₍₁₎=1 1110100，[y]₍₁₎=10110000。若整型变量z=2x+y/2，则z的机器数为( )。

A. 1 100000

B. 0 0100100

C. 1 0101010

D. 溢出

算数移位：关注有符号数值处理，移位过程中符号位保持不变。左移时，最高位的符号位被复制到移出位置；右移时，正数填充0，负数填充符号位的值。

逻辑移位：用于无符号数值处理，移位过程中不考虑符号位。左移和右移时，空出的位置均填充0。

移位之后进行计算没有发生溢出，选A

【2014统考真题】若x=103,y=-25，则下列表达式采用8位定点补码运算实现时，会发生溢出的是( )。

A. x+y

B. -x+y

C. x-y

D. -x-y

C为128，于是溢出

【2018统考真题】假定有符号整数采用补码表示，若int型变量x和y的机器数分别是FFFF FFDH和0000 041H，则x，y的值及x-y的机器数分别是( )。

A. x=-65,y=41,x-y的机器数溢出

B. x=-33,y=65,x-y的机器数为FFFF FF9DH

C. x=-33,y=65,x-y的机器数为FFFF FF9EH

D. x=-65,y=41,x-y的机器数为FFFF FF96H

-98，各位取反末尾加一结果为C

【2018统考真题】整数x的机器数为1101 1000，分别对x进行逻辑右移1位和算术右移1位操作，得到的机器数各是( )。

A. 1110 1100、1110 1100

B. 0110 1100、1110 1100

C. 1110 1100、0110 1100

D. 0110 1100、0110 1100

算数移位：关注有符号数值处理，移位过程中符号位保持不变。左移时，最高位的符号位被复制到移出位置；右移时，正数填充0，负数填充符号位的值。

逻辑移位：用于无符号数值处理，移位过程中不考虑符号位。左移和右移时，空出的位置均填充0。

于是选B

[2018统考真题]减法指令“sub R1, R2, R3”的功能为“(R1)-(R2)→R3”，该指令执行后将生成进位/借位标志CF和溢出标志OF。若(R1)= FFFF FFFFH，(R2)= FFFF FFOOH，则该减法指令执行后，CF与OF分别为（）。

A. CF=0, OF=0 B. CF=1, OF=0 C. CF=0, OF=1 D. CF=1, OF=1

无借位，无溢出，所以选A

【2023 统考真题】已知 x,y 为 int 类型，当 x = 100, y = 200 时，执行“x 减 y”指令得到的溢出标志 OF 和借位标志 CF 分别为 0,1，那么当 x = 10, y = -20 时，执行该指令得到的 OF 和 CF 分别为（）。

A.OF=0, CF=0 B.OF=0, CF=1 C.OF=1, CF=0 D.OF=1, CF=1

有借位，无溢出，所以选B

【2024 统考真题】C 语言代码段如下，执行该代码段后，j 的值是（）。

int i=32777;

short si=i;

int j=si;

A.-32777 B.-32759 C.32759 D.32777

【2024 统考真题】下列关于整数乘法运算的叙述中，错误的是（）。

A.用阵列乘法器实现的乘运算可以在一个时钟周期内完成

B.用 ALU 和移位器实现的乘运算无法在一个时钟周期内完成

C.变量与常数的乘运算可编译优化为若干移位及加/减运算指令

D.两个变量的乘运算无法编译转换为移位及加法等指令的循环实现

乘法可以通过加法实现，选D

[2020统考真题]有实现x*y的两个C语言函数如下：

unsigned umul(unsigned x,unsigned y) { return x*y; }
int imul(int x,int y) {return x * y; }

假定某计算机M中的ALU只能进行加法运算和逻辑运算。请回答下列问题。

1) 若M的指令系统中没有乘法指令，但有加减法和位移等指令，则在M上也能实现上述两个函数中的乘法运算，为什么？

多次加or减法可以模拟乘除

位移可以模拟乘除 2n

2) 若M的指令系统中有乘法指令，则基于ALU、位移器寄存器及相应控制逻辑实现乘法指令时，控制逻辑的作用是什么？

主要是编排指令运行的方式，就像是运算的次数以及种类

3) 针对以下三种情况：a) 没有乘法指令；b) 有使用ALU和位移器实现的乘法指令；c) 有使用阵列乘法器实现的乘法指令，函数umul()在哪种情况下执行的时间最长？在哪种情况下执行的时间最短？说明理由。

阵列最短，没有乘法指令最长

因为a占n个时钟周期，b少于a，而c只需要一个时钟周期

4) n位整数乘法指令可保持2n位乘积，当只取低n位作为乘积时，其结果可能发生溢出。当 n=32,x=231−1,y=2 时，有符号整数乘法指令和无符号整数乘法指令得到的 x×y 的2n位乘积分别是什么(用十六进制数表示)？此时函数umul()和imul()的返回结果是否溢出？对于无符号整数乘法运算，当仅取乘积的低n位作为乘法结果时，如何用2n位乘积进行溢出判断？

有符号位会溢出，无符号位不会，判断：最后的站位高于2n则会溢出

三.四则运算

3.1.补码运算

表达式如下：

补补补补补补[x+y]补=[x]补+[y]补(mod 2n)[x−y]补=[x]补+[−y]补(mod 2n)

这是补码加减运算的部件

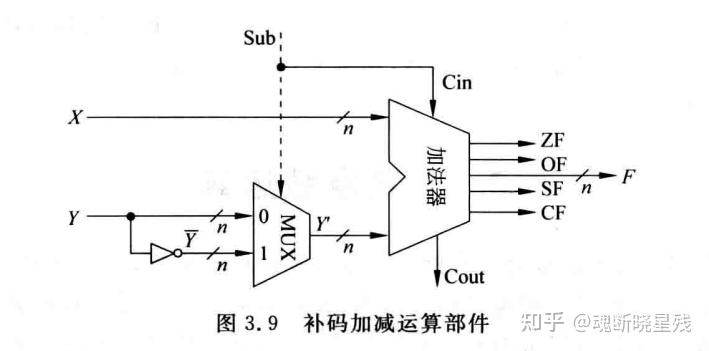
接下来我们看一道例题

例3.2 用4位补码计算“-7-6”和“-3-5”的值。

解：

补，补[−7]补=1001，[−6]补=1010

补，补[−3]补=1101，[−5]补=1011

补补补[−7−6]补=[−7]补+[−6]补=1001+1010=0011(+3)

补补补[−3−5]补=[−3]补+[−5]补=1101+1011=1000(−8)

所以严格判断溢出的方式：

(1)若符号位产生的进位 $C_n$ 与最高数值位向符号位的进位$C_n-1$不同，则产生溢出，即：

Overflow=Cn−1⊕Cn

(2)若两个加数的符号位相同，且与和的符号位不同，则产生溢出。即：

，Overflow=Xn−1，Yn−1F¯n−1+X¯n−1Y¯n−1Fn−1

我们做一道相关的真题

【2011统考真题】假定在一个8位字长的计算机中运行如下C程序段：

unsigned int x=134;
unsigned int y=246;
int m=x;
int n=y;
unsigned int z1=x-y;
unsigned int z2=x+y;
int k1=m-n;
int k2=m+n;

若编译器编译时将8个8位寄存器R1~R8分别分配给变量x,y,m,n,z1,z2,k1和k2.请回答下列问题(提示:有符号整数用补码表示)。

首先我们分析代码中所有的计算

134 = 128 + 6 = 1000 0110B，所以x的机器数为1000 0110B，因此R1的内容为86H。

246 = 255 - 9 = 1111 0110B，所以y的机器数为1111 0110B，

x-y=1000 0110 + 0000 1010=(0)1001 0000，

括号中为加法器的进位，因此R5的内容为90H。x+y=1000 0110+1111 0110=(1)0111 1100，括号中为加法器的进位，因此R6的内容为7CH。

m的机器数与x的机器数相同，皆为86H=1000 0110B，其值为-122.

m-n的机器数与x-y的机器数相同，皆为90H=1001 0000B，其值为-112

1)执行上述程序段后，寄存器R1、R5和R6的内容分别是什么(用十六进制表示)?

86H

90H

7CH

2)执行上述程序段后，变量m和k1的值分别是多少(用十进制表示)?

-122

-112

3)上述程序段涉及有符号整数加减、无符号整数加减运算，这四种运算能否利用同一个加法器辅助电路实现?简述理由。

由于加法器表达式如下：

补补补补补补[x+y]补=[x]补+[y]补(mod 2n)[x−y]补=[x]补+[−y]补(mod 2n)

所以可以判断加减

4)计算机内部如何判断有符号整数加减运算的结果是否发生溢出?上述程序段中，哪些有符号整数运算语句的执行结果会发生溢出?

判断溢出的方式：

(1)若符号位产生的进位 $C_n$ 与最高数值位向符号位的进位$C_n-1$不同，则产生溢出，即：

Overflow=Cn−1⊕Cn

(2)若两个加数的符号位相同，且与和的符号位不同，则产生溢出。即：

，Overflow=Xn−1，Yn−1F¯n−1+X¯n−1Y¯n−1Fn−1

然后呢

3.2补码乘除

补码乘法： 补补[x×y]补=[x×∑i=0n−1(Yi−1−Yi)2i]补

或者 补[x×∑i=0n−1(Yi−1−Yi)2−(n−i)]补

乘法器的逻辑结构

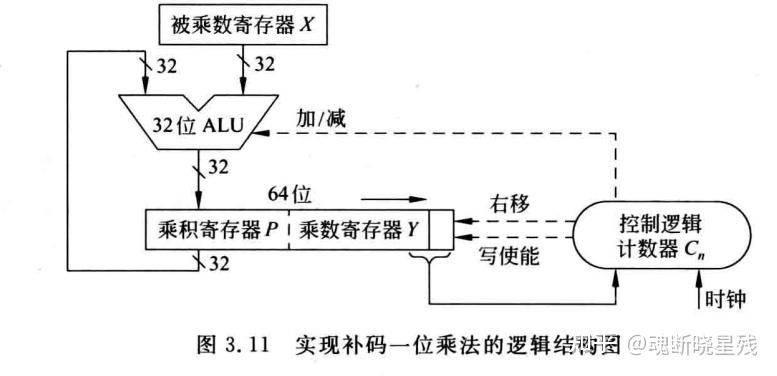
已知 补补[x]补=1101,[y]补=0110 ,要求用布斯乘法计算 补[x×y]补

于是答案为11101110