排序之——冒泡排序

冒泡排序

冒泡排序时比较简单并且容易理解的一种排序算法。

1. 冒泡排序的实现

冒泡排序时是一种交换排序，比较相邻的两个关键字，如果它们的顺序是错误的，则将它们交换过来，如此的重复，知道整个序列有序。当然冒泡排序有多种的实现。
这是最简单的一种实现。

void BubbleSort(int a[], int n) {
    int i, j, temp;
    for (i = 0; i < n - 1; i++) {
        for (j = 0; j < n - i - 1; j++) {
            if (a[j] > a[j + 1]) {
                temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
            }
        }
    }
}

这是冒泡排序的一种实现，其过程为：
1. 比较相同的元素，如果第一个比第二个大，那么久交换它们两个。
1. 对每一对相邻的元素都做同样的工作，从开始到结束，这样最后一个数字就是最大的那个数字了。
1. 重复上述步骤，倒数第二位数字就是次大的数字…

2. 冒泡排序的另一种实现

上面的冒泡排序中每一趟都会找到一个“最大值”，那么也可以每趟找一个“最小值”。

void BubbleSort(int a[], int n) {
    int i, j, temp;
    for (i = 0; i < n - 1; i++) {
        for (j = n - 2; j >= i; j--) {
            if (a[j] > a[j + 1]) {
                temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
            }
        }
    }
}

上面的这个算法是正宗的冒泡排序。它的过程符合冒泡的过程。加入，要排序的数组为{5,4,3,2,1}。则它的第一趟过程如下：

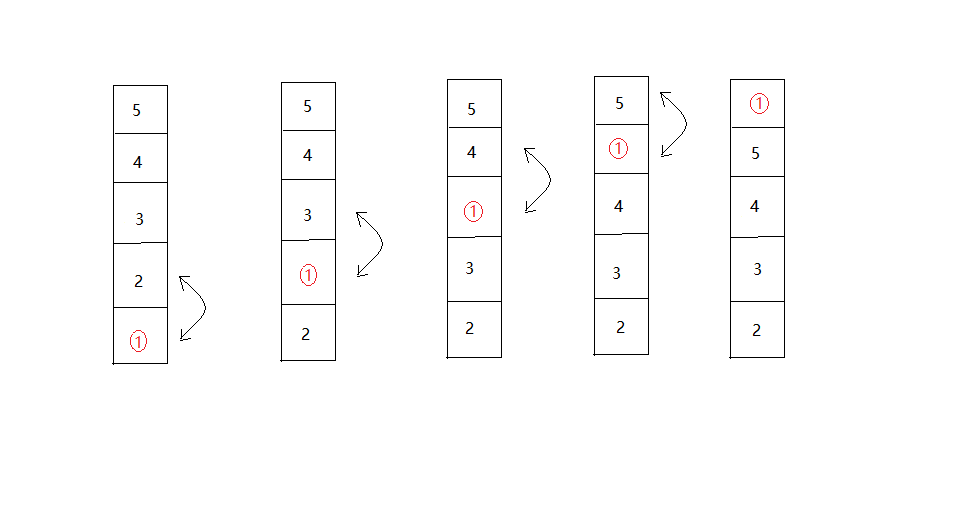
从上图中可以看出冒泡排序的名字的由来。

3. 冒泡排序的优化

想想一种情况，加入带排序的数组是{4,1,2,3,5}，不难发现是需要一趟排序，这个数组就已经有序了，不需要在进行排序了，但是按照之前的代码，需要进行n-1趟排序，显然，这里可以进行优化。优化也很简单，如果排序中有一趟排序没有元素的交换，那么显然就已经是有序的了。算法的实现如下：

void BubbleSort(int a[], int n) {
    int i, j, temp, flag = 1;
    for (i = 0; i < n - 1 && flag; i++) {
        flag = 0;
        for (j = n - 2; j >= i; j--) {
            if (a[j] > a[j + 1]) {
                temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
            }
            flag = 1; 
        }
    }
}

4. 冒泡排序的时间复杂度

最好的情况是需要排序的数组本身就是有序的，不需要进行交换，它的时间复杂度是：O(n)。
最坏的情况是，需要排序的数组是一个逆序的，那么每趟排序都需要进行关键字的交换，它的时间复杂度是$O(n^2)$。
在这里不得不提的是排序的稳定性。那么什么是排序的稳定性呢？

5. 排序的稳定性

假设现在要对一个班级的学生成绩排序，最后按照这个成绩定名次。一般来说，如果两个人的成绩相同，那么肯定是学号小的排在前面，学号大的排在后面。那么对于排序来说，如果两个出现两个关键字相同的情况，那么排好序之后如果下标小的在前，下标大的在后，那么就说这个排序是稳定的。也就是说，假设$a_i=a_j$,且$a_i$在排序前的序列中领先于$a_j$(i>j)，如果在排序后的序列中$a_i$仍领先于$a_j$，那么成这个序列是有序的。
原文链接