4.1基本流程
今天学习一种常见的机器学习方法——决策树。什么东西呢,我觉得看一下下面这个图就知道什么回事了(图是用别的博主的)
决策树包含一个根结点,若干内部结点和叶节点。叶节点表示决策结果(见还是不见),其他结点对应一个属性测试。可以看到,除了根结点包含所有的样本外,每经过一个属性测试,下面的节点就会只包含满足测试的样本,样本数越来越少。从根结点到叶节点就对应了一个测试序列。
看一下决策树的基本算法:
这个算法可以从头到尾自己跟着它走一遍,大概知道什么意思,然后后面会有实际的构造决策树,对照着成型的决策树,自己再走一遍算法,如果能完美的和对照的决策树生成过程吻合,那我觉得就是理解了。
注意看一下算法的第8步,从属性集里面选择最优划分属性a*。什么意思呢?就是比如上面那个小姑娘相亲决策树,第一个测试属性是什么?年龄。那为什么不能使先测试身高呢?其实就是小姑娘无形中做了第8步算法——选了最优划分属性,人家认为年龄是最好的划分男生的属性。我们的算法第8步也是这个工作,那么我们这么选择呢?
4.2 划分选择
这一节就来解决怎么选择最优划分属性的问题。
摆几个定义:
Ent(D)是数据集D的信息熵。D里面有|y|个类别,每一类占比pk。我们都学过熵,表示的是一个系统的混乱程度。所以我们可以这么说,D越纯,信息熵越小。
Gain(D,a)是用属性a来划分D获得的信息增益。V是属性a的可能取值个数,如{a1,a2,…,aV}。Dv是D的子集,包含在a上取值为av的样本。一般说,这个信息增益越大,意味着用属性a划分获得的“纯度提升”越大。
所以我们有办法解决怎么选择最优划分属性的问题了:
这就是我们的选择标准,每个属性我都给你算一个信息增益,谁大我要谁。(这个准则的算法我们叫"ID3决策树算法")
下面给一个数据集和一个基于该数据集用ID3算法生成的决策树。具体过程不写了,自己可以尝试着算一算,看能不能捣鼓出来,也顺便复习一下上面的基本算法。
西瓜数据集:
生成的决策树:
补充一点,我个人觉得书上这个决策树第二层中间的节点“触感=?”,下面的叶子节点反了。
上面的信息增益其实不错,但还不是太好。什么意思?我们的原则是要挑信息增益最大的属性出来,现在假设把上面西瓜数据集最左一列编号也当属性计算信息增益,会发现这个“编号”竟然是信息增益最大的。这意味着我要拿这么个莫名其妙的玩意儿当第一个属性结点。这是没有意义的。为什么会这样呢?因为简单想一下,这个编号属性可取的属性值有17个,也就是有17个分支,每个分支结点只有一个样本,简直比特仑苏还纯,有木有。
我们发现信息增益是对类似“编号”这样属性值可取数较多的属性有偏好。而这种偏好我们也看到有不好的影响。
怎么办呢,推出一个新的标准——增益率。
不解释了,也是越大越好。
补充一下,增益率也有缺点,对属性值比较少的属性偏爱。所以我们的策略是:先挑出所有信息增益高于平均水准的属性,再从挑出的里面选出增益率最大的属性。可以理解成把信息增益和增益率结合一下嘛。
对了,用增益率当准则的是C4.5决策树算法。
说了ID3和C4.5算法,再讲一个CART决策树算法吧:
这个CART用的选择标准是基尼指数。
首先是基尼值:
Gini(D)越小,数据集D纯度越高。
属性a的基尼指数:
属性集里谁的基尼指数越小,我们选哪个。
4.3 剪枝处理。
这一步是干嘛的呢——防止过拟合。我们有提过过拟合不好。体现在这各决策树里面就是分支太多啦,好多诡异的性质都被你学到了,这个学习器没有普遍性了。
既然分支太多了,我们就剪吧,这就是“剪枝处理”。怎么剪呢?面对一个结点,你拿什么理由剪掉它?凭什么?前面有说留出法对吧,我们就用这个留出法,选一部分样本做测试样本,面对一个结点,考虑它在和不在泛化性能有没有变化,做出剪与不剪的决定。
“预剪枝”:决策树生成过程中,每个结点划分前,我要算一下,划分和不划分泛化性能的差别。划分后性能提升了就果断划分,反之不化了。
“后剪枝”:先按以前的办法正常生成决策树,再自底向上考察非叶子结点:把它换成叶子结点,看有没有提升性能……
详细的例子就不写了,分析一波“预剪枝”和“后剪枝”的区别吧:
预剪枝就是你可以看到,生成过程中发挥作用,结果往往是很多结点都没展开,分支很少。优点当然是减少计算量啦。降低过拟合风险;缺点是这种方法本质是“贪心的”,只考虑眼前的利益,导致决策树可能会欠拟合。
后剪枝是等人家决策树正常生成完了再去发挥作用的啊,那就显然运算开销大;优点是欠拟合风险小,保留的分支多一点嘛。泛化性能一般优于预剪枝。
所以我理解的是在训练时间开销不是那么吃紧的情况下,后剪枝似乎是个更好的选择。
4.4连续值和缺失值
前面讨论的都是离散属性,如果属性值是连续的怎么办?比如说西瓜的密度范围是(0,1)。在这区间内任意值都可能出现,总不可能那么多分支。怎么办呢?
我们先假设数据集的样本属性密度有这么几个{0.1,0.3,0.5,0.9}。4个值,我们计算3个划分候选点,即每相邻两个数中点,这里就得到候选划分点{0.2,0.4,0.7}。
这个划分点就是小于它的扔进反例集合,大于它的扔进正例集合。形成两个分支。
当然候选划分点你要计算出各自的信息增益,最大的就是正式划分点。
还有一点注意的是,前面离散属性,用过一次后就不能在用了,连续属性不必遵守这个约束。
现实中,种种原因,你拿到的数据集里面往往属性值是不完整的。比如这样:
如果只要有缺失你就舍弃,那么原来17个样本你只能使用4个来训练,肯定不好。
解决方法:
4.5 多变量决策树
前面介绍的决策树有个特点,就是你把它画到属性空间里(前面说过d个属性的样本对应d维空间一个点,每个坐标轴是一个属性),决策树的分类边界均与坐标轴平行。
对西瓜的两个属性——含糖量和密度生成决策树,像这样:
分类边界是这样的:
这里还只有两个属性,如果10个,20个呢?可想而知,分类边界会有很多段,决策树时间开销极大。
解决方法,直接看这个决策树:
有木有很聪明,管你有多少个属性,我全用一个式子给你捏一块。专业点就是
人家这种方法生成的分类边界长这样:
可以看到,它是斜的,很有灵气啊。比一段一段平行于坐标轴的边界简洁多了啊有木有。
哎,我本来是不想直接从书上截图的,觉得不好(一方面觉得侵权侵的太明显……,一方面就很啰嗦)。但是CSDN编辑器太low了啊,用word公式编辑又好麻烦,而且更气的是编辑的公式还不能直接连同文本粘贴过来,得存为图片插进来……坑爹啊,有木有。
反正写这个东西只是想锻炼一下自己的性子,也想学的更细致一些。仅做学习之用。而且我发现我有的东西讲的很啰嗦,以后可能就不假想别人阅读了,我会按照自己的思路和节奏来写,这样也能提高效率。











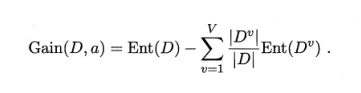




























 1875
1875

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








