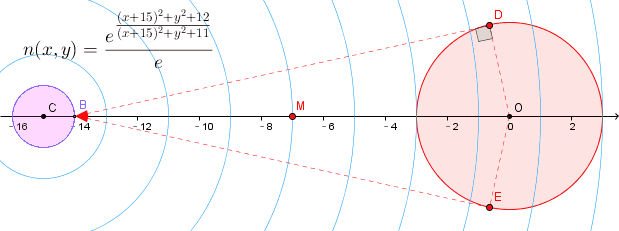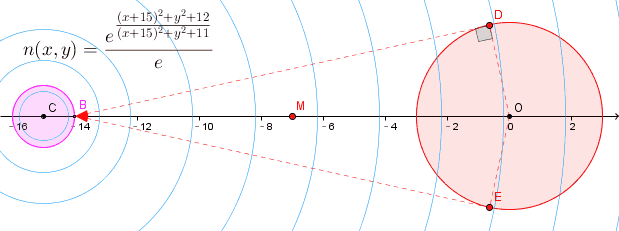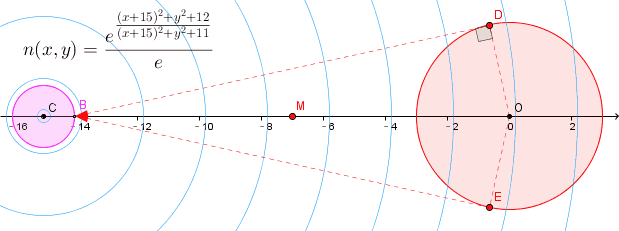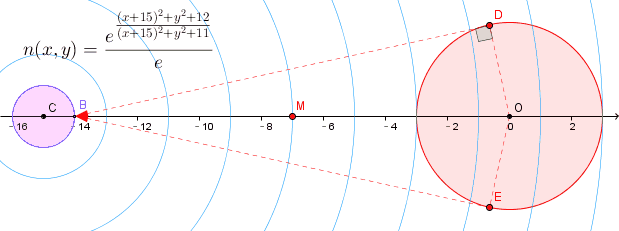
问题是这样的,如图,圆O的半径为3, 圆C半径为1;
O的坐标(0,0), C坐标(-15,0), B的坐标(-14,0)
圆盘O是一个发光源,那么,如果透明介质处处的折光率都是常数,
则从B点观察圆盘O时,可以看到上边界对应于BD,下边界对应BE,都是圆O的切线;
现在假设介质的折光指数是二元函数 n(x,y)
求在这种折光指数连续变化的透明光学介质中,从B点观察发光圆盘O,对应的上边界点和下边界点到B点的光线的路径曲线.
或者, 只求上下边界光线到达B点时它们各自对应的光线曲线的斜率.
从Fermat原理, 可以很容易把问题转化成变分问题, 并利用Euler-Lagrange方程把它写成一个二阶非线性常微分方程:
已经知道 y(-14)=0, 只须再知道 y(x)在 x=-14的一阶导数 y'(-14) 即可以容易得到数值解, 问题在于,这个不容易得到;
如果用近似的y'(-14)计算一系列的数值曲线出来,取跟圆O相切的一个也可以,但是太复杂了点;








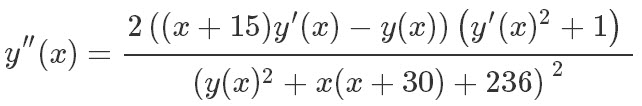















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








