拉宾（Rabin）公钥

拉宾公钥的原理是基于拉宾加密系统，它使用了两个大素数的乘积作为公钥，而私钥则是这两个大素数的因子。具体原理如下：

1. 选择两个大素数p和q，并计算它们的乘积n=p*q。
2. 计算φ(n)=(p-1)*(q-1)，其中φ(n)是欧拉函数。
3. 选择一个整数e，使得1<e<φ(n)，且e与φ(n)互质。
4. 计算e的模逆d，使得e*d ≡ 1 (mod φ(n))。
5. 公钥是(n, e)，私钥是(d)。

使用公钥加密信息时，将信息m的e次方对n取模得到密文c，即c ≡ m^e (mod n)。 使用私钥解密密文时，将密文c的d次方对n取模得到原始信息m，即m ≡ c^d (mod n)。

拉宾公钥的安全性基于大整数分解的难度，即使知道公钥(n, e)，也很难通过分解n来得到私钥d。因此，拉宾公钥系统被广泛应用于加密通信和数字签名等领域。

核心的算法如下（字有点丑：

 

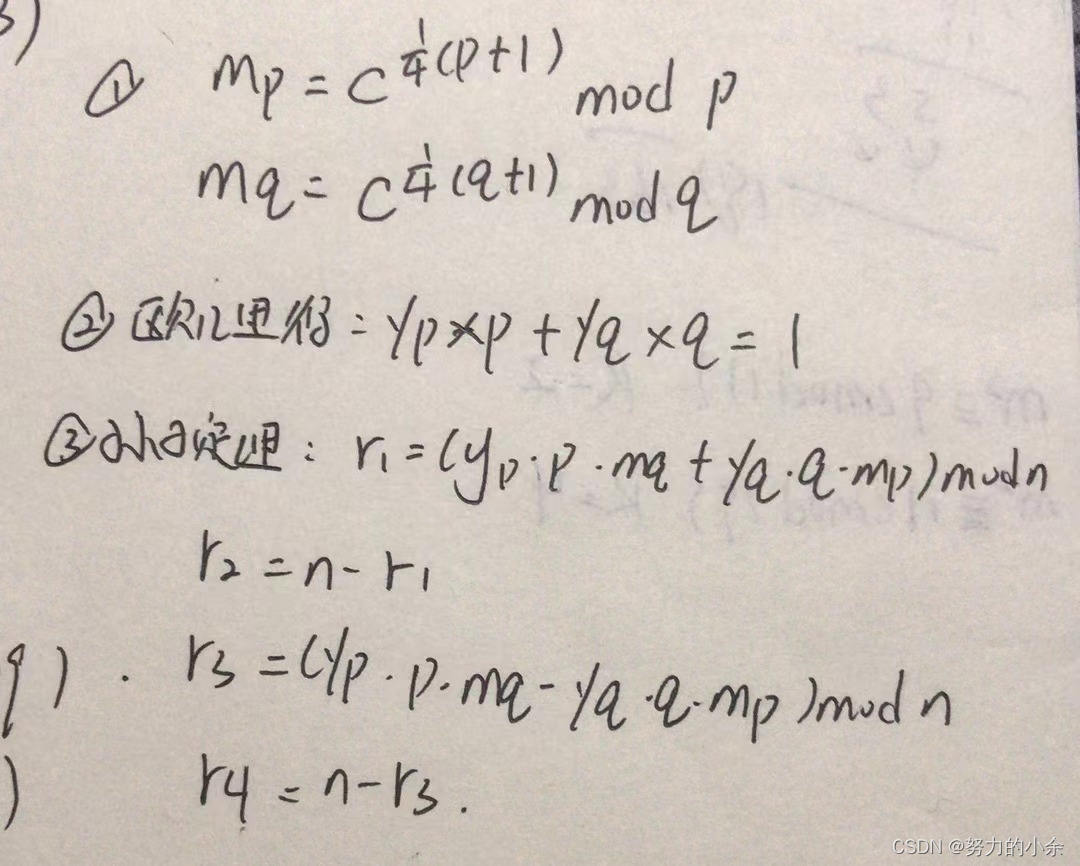
import random
#求大素数p，q
def random_primes() -> int:
    while(True):
        flag = False
        x = random.randint(0,100)
        if ((x - 3) % 4 == 0):
            for i in range(2,x - 1):
                n = True
                if x % i == 0:
                    n = False
                    break
            if n != False:
                flag = True
        if flag == True:
            return x

#加密
def encrypt(n) -> [int,int]:
    m = random.randint(1,n-1)
    # m = 102
    C = pow(m,2,n)
    return m,C

def ex_gcd(a,b) -> [int,int,int]: #欧几里得算法求最大公约数
    if b == 0:
        return 1,0,a
    else:
        s,t,r = ex_gcd(b, a % b)
        s,t = t,(s - (a // b) * t)
        return s,t,r

def decrypt(p,q,C) -> [int,int,int,int]: #解密
    Mp = pow(C,(p + 1) // 4) % p
    Mq = pow(C,(q + 1) // 4) % q

    #使用拓展欧几里得算法求得最大公约数
    Yp,Yq,gcd = ex_gcd(p,q)
    print(Yp,Yq)
    print("最大公约数为{}".format(gcd))
    #孙子定理,求四个解
    r1 = ((Yp * p * Mq) + (Yq * q * Mp)) % n
    r2 = n - r1
    r3 = ((Yp * p * Mq) - (Yq * q * Mp)) % n
    r4 = n - r3

    return r1,r2,r3,r4

def finf_crypt(r1,r2,r3,r4,m):
    thislist = []

    thislist.append(r1)
    thislist.append(r2)
    thislist.append(r3)
    thislist.append(r4)

    if m in thislist:
        print("---------------------------------------------")
        print("已从四个解中找到明文m = {}".format(m))
    else:
        print("为从中找到明文，解密失败!!!")

if __name__ == '__main__':
    p = random_primes()
    q = random_primes()
    # p = 11
    # q = 19
    n = p * q

    m,C = encrypt(n)
    r1,r2,r3,r4 = decrypt(p,q,C)

    print("密钥生成: 找到大素数p = {},q = {},将n = {}作为公钥".format(p,q,n))
    print("加密: 将明文m = {},密文C = {}发送出".format(m,C))
    print("解密后所有的解为r1 = {},r2 = {},r3 = {},r4 = {}".format(r1,r2,r3,r4))

    finf_crypt(r1,r2,r3,r4,m)

运行随机案例：