kkksc03考前临时抱佛脚详解｜01背包与双脑并行优化（洛谷P2392 ）-CSDN博客

本文链接：https://blog.csdn.net/stillwatersss/article/details/153686036

一、问题引入（痛点场景）

真题溯源：洛谷P2392 kkksc03考前临时抱佛脚
用户痛点：

"如何将题目合理分配给左右大脑？如何最小化完成时间？s≤20时如何避免指数级复杂度？"

这是典型的任务分配优化问题，在CSP-J/S竞赛中考查选手的动态规划思维和问题建模能力。题目核心是将每科的题目分配给左右大脑，使得完成时间最短。

竞赛价值：此类任务分配问题在近年竞赛中出现频率较高，占分约10-15分，是必须掌握的优化算法题型。

二、核心算法分析

2.1 问题本质：最小化最大负载

关键洞察：

左右大脑可以同时处理同一科目的题目
完成时间由较慢的大脑决定（最大负载）
目标是最小化每科的最大负载之和

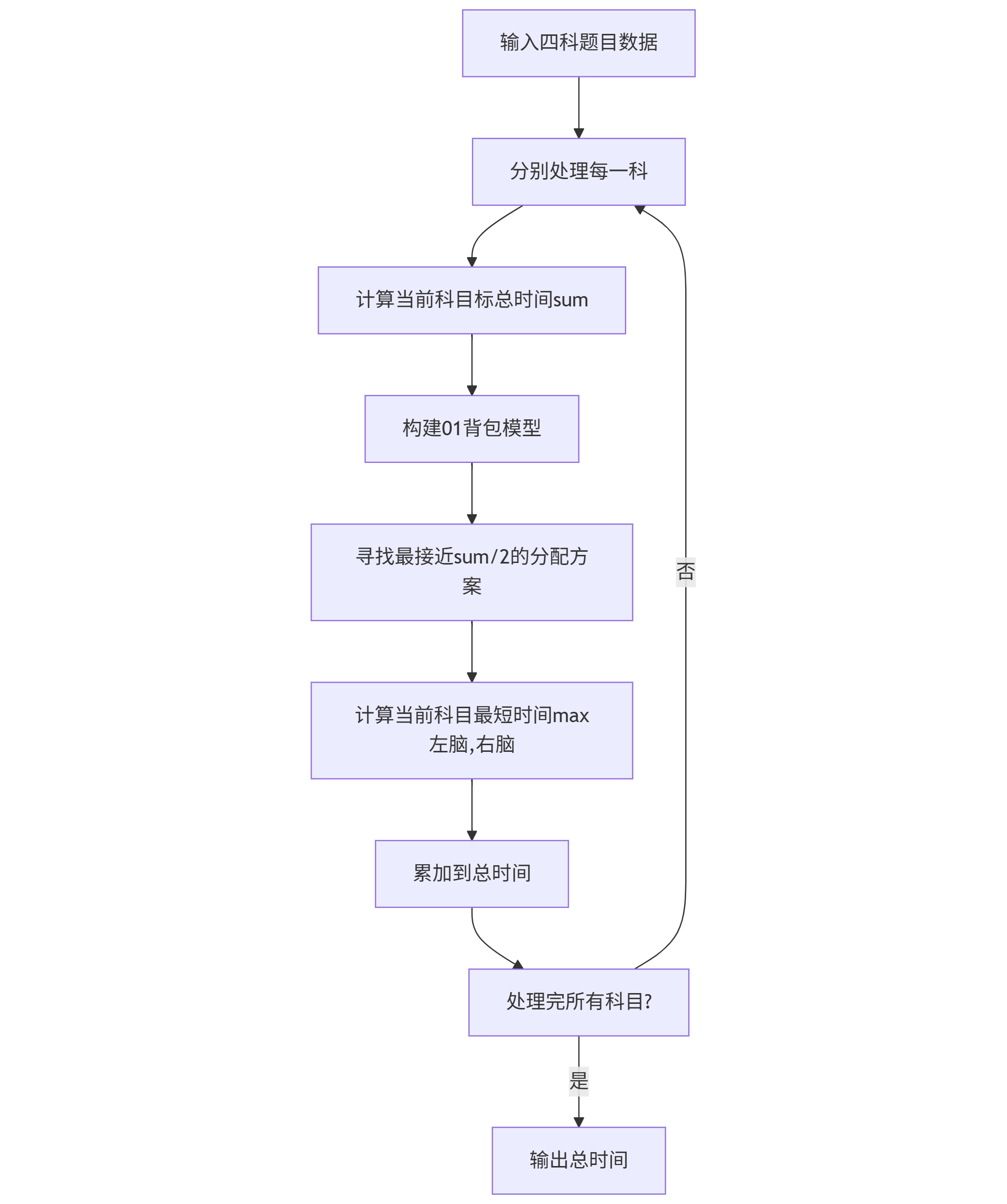
2.2 算法思路详解

01背包建模：

背包容量：总时间的一半（sum/2）
物品价值：每道题的耗时
目标：找到最接近sum/2的分配方案
最短时间 = max(左脑时间, 右脑时间) = max(dp[sum/2], sum - dp[sum/2])

三、代码实现详解

3.1 标准解法（01背包优化）

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;

int main() {
    int s1, s2, s3, s4;
    cin >> s1 >> s2 >> s3 >> s4;
    
    int total_time = 0;
    
    // 处理每一科
    for (int subject = 0; subject < 4; subject++) {
        int n;
        if (subject == 0) n = s1;
        else if (subject == 1) n = s2;
        else if (subject == 2) n = s3;
        else n = s4;
        
        vector<int> times(n);
        int sum = 0;
        
        // 读取当前科目的题目耗时
        for (int i = 0; i < n; i++) {
            cin >> times[i];
            sum += times[i];
        }
        
        // 01背包：寻找最接近sum/2的分配
        vector<bool> dp(sum / 2 + 1, false);
        dp[0] = true;
        
        for (int i = 0; i < n; i++) {
            for (int j = sum / 2; j >= times[i]; j--) {
                if (dp[j - times[i]]) {
                    dp[j] = true;
                }
            }
        }
        
        // 找到最接近sum/2的可达时间
        int left_time = 0;
        for (int j = sum / 2; j >= 0; j--) {
            if (dp[j]) {
                left_time = j;
                break;
            }
        }
        
        int right_time = sum - left_time;
        total_time += max(left_time, right_time);
    }
    
    cout << total_time << endl;
    return 0;
}

3.2 优化解法（bitset优化）

#include <iostream>
#include <vector>
#include <bitset>
#include <algorithm>
using namespace std;

const int MAX_SUM = 1200; // 20×60=1200

int main() {
    int s[4];
    cin >> s[0] >> s[1] >> s[2] >> s[3];
    
    int total = 0;
    
    for (int subject = 0; subject < 4; subject++) {
        vector<int> times(s[subject]);
        int sum = 0;
        
        for (int i = 0; i < s[subject]; i++) {
            cin >> times[i];
            sum += times[i];
        }
        
        // 使用bitset优化空间和时间
        bitset<MAX_SUM + 1> dp;
        dp[0] = 1;
        
        for (int time : times) {
            dp |= dp << time;
        }
        
        // 寻找最接近sum/2的可行解
        int best = 0;
        for (int j = sum / 2; j >= 0; j--) {
            if (dp[j]) {
                best = j;
                break;
            }
        }
        
        total += max(best, sum - best);
    }
    
    cout << total << endl;
    return 0;
}

四、算法原理深度解析

4.1 01背包问题转化

问题等价性：

左脑时间：背包中物品的重量和
右脑时间：总重量 - 背包重量
目标：min(max(背包重量, 总重量-背包重量))

数学证明：

设总重量为S，背包重量为x
完成时间 = max(x, S-x)
当x接近S/2时，max(x, S-x)最小

4.2 复杂度分析

时间复杂度：O(n×sum)

每科：n次循环，sum次操作
最坏情况：20×1200=24000次操作
四科总计：4×24000=96000次操作

空间复杂度：O(sum)

使用一维dp数组或bitset优化

五、避坑指南与调试技巧

5.1 常见错误分析

错误1：dp数组初始化错误

// 错误：忘记初始化dp[0]=true
vector<bool> dp(sum/2+1, false);
// 缺少dp[0]=true;

// 正确：确保0重量是可达的
dp[0] = true;

错误2：背包循环顺序错误

// 错误：正序循环导致物品重复使用
for (int j = times[i]; j <= sum/2; j++) {  // 错误！

// 正确：逆序循环保证01背包性质
for (int j = sum/2; j >= times[i]; j--) {
    if (dp[j - times[i]]) {
        dp[j] = true;
    }
}

5.2 测试用例验证

void testCases() {
    // 用例1：题目样例
    // 科目1：[5] → 时间5
    // 科目2：[4,3] → 最佳分配：4 vs 3 → 时间4
    // 科目3：[6] → 时间6  
    // 科目4：[2,4,3] → 最佳分配：2+3=5 vs 4 → 时间5
    // 总计：5+4+6+5=20 ✓
    
    // 用例2：单题目科目
    // 用例3：全相同耗时题目
    // 用例4：边界值测试s=20, time=60
}

六、性能优化建议

6.1 bitset优化技巧

位运算加速：

bitset<MAX_SUM> dp;
dp[0] = 1;
for (int time : times) {
    dp |= dp << time;  // 位运算并行处理
}

6.2 内存访问优化

局部变量缓存：

for (int subject = 0; subject < 4; subject++) {
    int n = s[subject];  // 缓存当前科目题目数
    vector<int> local_times = times[subject];  // 局部拷贝
    // ... 处理逻辑
}

七、竞赛应用与扩展

7.1 同类题型推荐

洛谷P1048：采药（01背包基础）
洛谷P1060：开心的金明（01背包应用）
洛谷P1510：精卫填海（背包变形）

7.2 算法思维拓展

从双脑分配到更复杂问题：

掌握01背包的问题建模技巧
理解最小化最大值的优化思想
学会使用bitset进行状态压缩

竞赛技巧提升：

熟练识别背包问题变种
掌握空间优化技巧
注意边界条件和初始化

🔥 关注我，解锁CSP-J/S竞赛全攻略 🔥

（每日更新高频考点 + 精选真题解析，助你轻松备赛！）
👇 点击关注 → 立即提升竞赛战力 👇
[https://blog.csdn.net/stillwatersss]

📚 专栏亮点抢先看

高频考点突破
- 每日一题：精选洛谷/LeetCode CSP-J/S经典真题，附详细题解与时间复杂度优化技巧
- 考点拆解：动态规划、图论、字符串算法等核心专题深度剖析，直击竞赛命题规律
- 实战模板：限时领取《C++竞赛模板大全》👉 关注后私信回复“模板”获取
备赛效率翻倍技巧
- 从O(n²)到O(n)：独家算法优化套路，解决TLE超时问题
- 考场避坑指南：常见失分点分析 + 数据边界处理技巧
- 互动答疑：评论区留言题目编号，优先解析你的个性化难题
独家福利🌟
- 粉丝专享：高价值文章设为 “仅粉丝可见”（如《CSP-J/S近5年考点分布与预测》）
- 资料包：关注后私信 “资料” 领取 竞赛真题库+调试代码工具包