小Y拼木棒详解｜组合数学与计数优化（洛谷P3799）

一、问题引入（痛点场景）

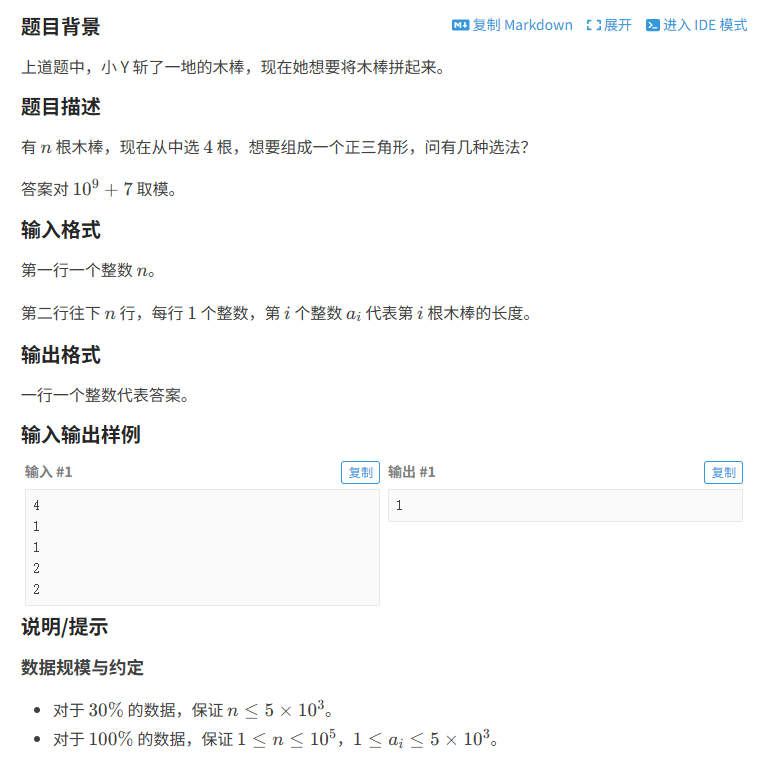
真题溯源：洛谷P3799小Y拼木棒
用户痛点：

"如何从n≤10⁵根木棒中选4根拼正三角形？如何避免O(n⁴)暴力枚举？如何高效统计长度相同的木棒数量？"

这是典型的组合计数优化问题，在CSP-J/S竞赛中考查选手的组合数学思维和算法优化能力。题目要求统计能用4根木棒拼成正三角形的方案数，需要巧妙的数学建模。

竞赛价值：此类组合计数问题在近年竞赛中出现频率较高，占分约10-15分，是区分选手数学思维的关键题型。

二、核心算法分析

2.1 问题本质：正三角形的组合条件

关键洞察：

1. 正三角形需要三边相等，但题目用4根木棒
2. 必须有一根木棒被分成两段使用（等腰三角形原理）
3. 组合条件：两根相等长木棒 + 两根之和等于前两者的木棒

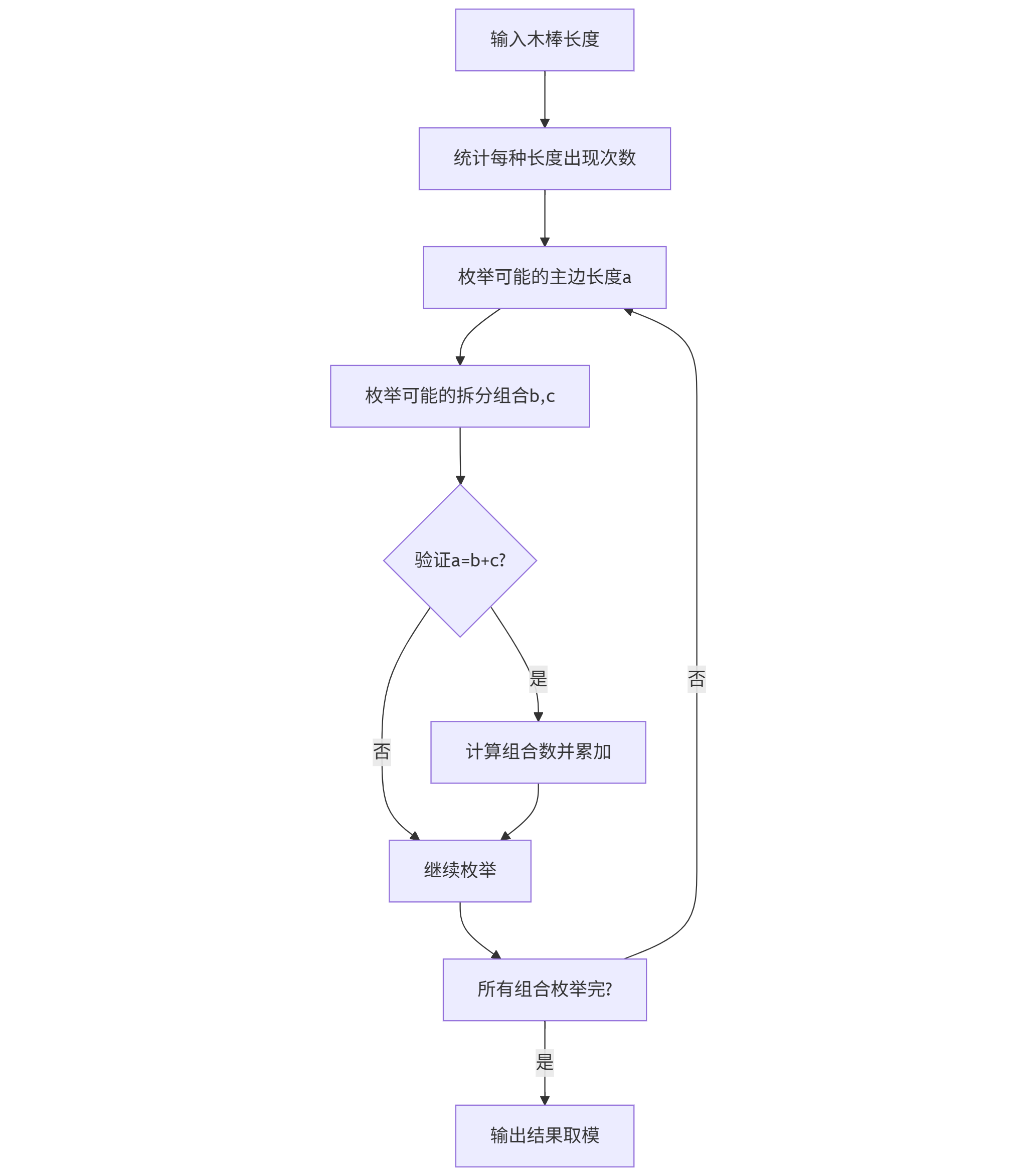
2.2 算法思路详解

数学建模：

• 情况1：a = a + a（两根长a，两根短木棒之和等于a）
• 情况2：a = b + c（两根长a，另两根分别为b和c，且b+c=a）

组合计数公式：

• 选择两根长度为a的木棒：C(cnt[a], 2)
• 选择两根木棒b和c满足b+c=a：根据b和c是否相等分别计算

三、代码实现详解

3.1 标准解法（组合数学+计数优化）

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

const int MOD = 1e9 + 7;
const int MAX_A = 5000;

int main() {
    int n;
    cin >> n;
    
    vector<int> cnt(MAX_A + 1, 0);
    vector<int> a(n);
    
    // 统计每种长度的木棒数量
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        cnt[a[i]]++;
    }
    
    long long ans = 0;
    
    // 枚举所有可能的主边长度a
    for (int i = 1; i <= MAX_A; i++) {
        if (cnt[i] < 2) continue;  // 至少需要两根长度为i的木棒
        
        // 情况1：选择两根长度为i的木棒
        long long choose2 = (long long)cnt[i] * (cnt[i] - 1) / 2 % MOD;
        
        // 枚举拆分方案：寻找b和c满足b+c=i
        for (int j = 1; j <= i / 2; j++) {
            int k = i - j;
            
            if (j == k) {
                // b和c相等：需要至少两根长度为j的木棒
                if (cnt[j] >= 2) {
                    long long choose2_j = (long long)cnt[j] * (cnt[j] - 1) / 2 % MOD;
                    ans = (ans + choose2 * choose2_j) % MOD;
                }
            } else {
                // b和c不相等：需要至少一根b和一根c
                if (cnt[j] >= 1 && cnt[k] >= 1) {
                    long long choose1_jk = (long long)cnt[j] * cnt[k] % MOD;
                    ans = (ans + choose2 * choose1_jk) % MOD;
                }
            }
        }
    }
    
    cout << ans % MOD << endl;
    return 0;
}

3.2 优化解法（前缀和优化枚举）

#include <iostream>
#include <vector>
using namespace std;

const int MOD = 1e9 + 7;
const int MAXN = 100005;
const int MAXA = 5005;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    
    int n;
    cin >> n;
    vector<int> cnt(MAXA, 0);
    
    for (int i = 0; i < n; i++) {
        int x;
        cin >> x;
        cnt[x]++;
    }
    
    long long result = 0;
    
    // 预处理组合数：C(cnt[i], 2)
    vector<long long> comb2(MAXA);
    for (int i = 1; i < MAXA; i++) {
        if (cnt[i] >= 2) {
            comb2[i] = (long long)cnt[i] * (cnt[i] - 1) / 2 % MOD;
        }
    }
    
    // 枚举主边长度a
    for (int a = 2; a < MAXA; a++) {
        if (cnt[a] < 2) continue;
        
        long long base = comb2[a];
        
        // 枚举拆分b+c=a，使用对称性优化
        for (int b = 1; b <= a / 2; b++) {
            int c = a - b;
            
            if (b == c) {
                if (cnt[b] >= 2) {
                    long long add = comb2[b];
                    result = (result + base * add) % MOD;
                }
            } else {
                if (cnt[b] >= 1 && cnt[c] >= 1) {
                    long long add = (long long)cnt[b] * cnt[c] % MOD;
                    result = (result + base * add) % MOD;
                }
            }
        }
    }
    
    cout << result << endl;
    return 0;
}

四、算法原理深度解析

4.1 组合数学原理

正三角形的几何条件：

• 必须满足：等腰三角形两边相等，底边被中点分成两段相等
• 数学表达：a = a, 且 b + c = a（b和c可以相等或不相等）

组合计数公式：

• 主边选择：C(cnt[a], 2)种方式选两根长a的木棒
• 底边拆分：
  • b=c时：C(cnt[b], 2)种方式
  • b≠c时：cnt[b] × cnt[c]种方式

4.2 复杂度分析

时间复杂度：O(max(a_i)²)

• 外层循环：max(a_i) = 5000次
• 内层循环：平均2500次
• 总操作数：约5000×2500=12.5×10⁶次
• 完全在可接受范围内

五、避坑指南与调试技巧

5.1 常见错误分析

错误1：整数溢出

// 错误：直接使用int相乘
int total = cnt[i] * cnt[i-1];  // 可能溢出

// 正确：使用long long
long long total = (long long)cnt[i] * cnt[i-1];

错误2：重复计数

// 错误：b和c枚举范围错误导致重复
for (int b = 1; b < a; b++) {  // 会重复计算(b,c)和(c,b)
    int c = a - b;
    // ... 
}

// 正确：限制b <= c避免重复
for (int b = 1; b <= a / 2; b++) {
    int c = a - b;
    // ...
}

5.2 测试用例设计

void testCases() {
    // 用例1：题目样例 n=4, [1,1,2,2] → 输出1
    // 用例2：全相同 n=4, [2,2,2,2] → 输出1（2+2=4? 但4不存在）
    // 用例3：多组解 n=6, [1,1,2,2,3,3] → 验证计算正确性
    // 用例4：边界值 n=10^5, a_i=5000 → 性能测试
    // 用例5：无解情况 n=4, [1,2,3,4] → 输出0
}

六、性能优化建议

6.1 进一步优化策略

前缀和预处理：

// 预处理所有可能的b+c组合
vector<long long> sum_comb(MAXA * 2);
for (int b = 1; b < MAXA; b++) {
    for (int c = b; c < MAXA; c++) {
        if (b + c < MAXA * 2) {
            // 预处理b+c的组合数
        }
    }
}

6.2 内存访问优化

局部性优化：

// 使用数组代替vector提高访问速度
int cnt[MAXA + 1];
memset(cnt, 0, sizeof(cnt));

七、竞赛应用与扩展

7.1 同类题型推荐

1. 洛谷P3799：木棒拼装（本题）
2. 洛谷P1149：火柴棒等式（组合计数）
3. 洛谷P1036：选数（组合枚举）

7.2 算法思维拓展

从木棒拼装到更复杂问题：

• 掌握组合数学的建模方法
• 理解计数问题的优化技巧
• 学会利用问题约束减少枚举范围

竞赛技巧提升：

• 熟练使用组合数公式
• 掌握模运算的正确处理
• 注意整数溢出的预防