手机整机测试

前言

做了一段时间的手机整机测试工作，虽然没有全面的去做，毕竟手机整机测试涉及的方方面面非常的广泛，我只负责其中的一小部分，比如功耗和Appium Automation部分，当然也设计Monkey相关工具的使用。

现简单汇总一下手机整机测试的一些信息点，比较粗略的记录一下主要测试点/方向。

概述

手机的整机测试（也称为手机全面测试或手机集成测试）是确保手机在各个方面都符合预期性能和质量标准的过程。这通常包括硬件、软件和用户界面的测试。

XMind思维导图

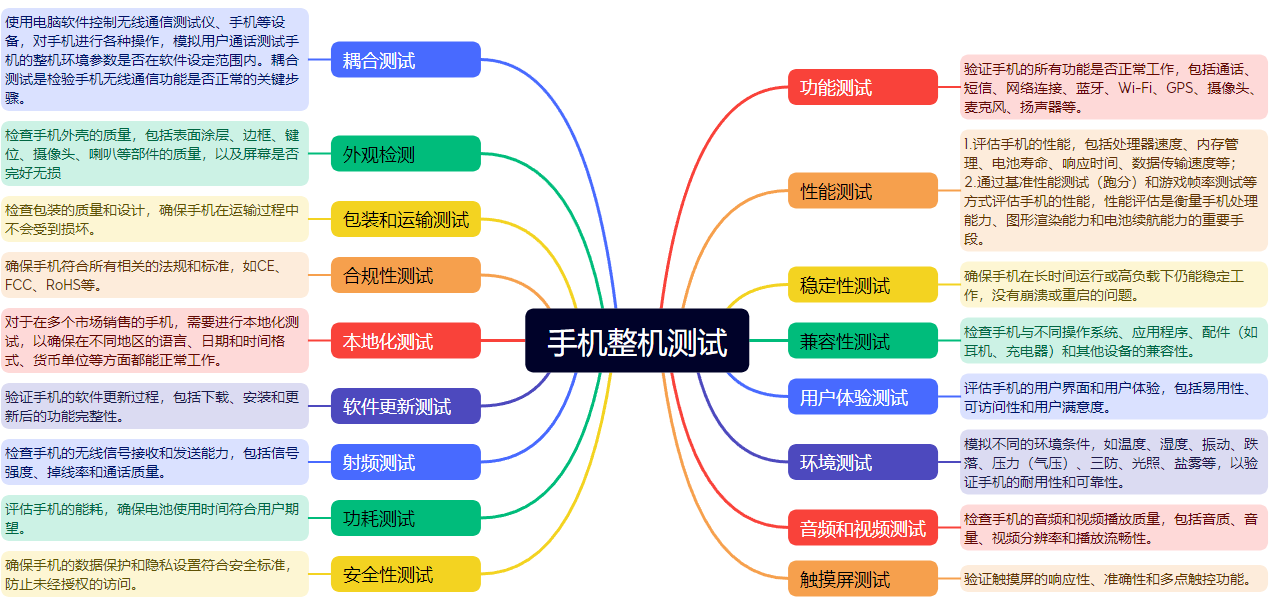
来源: Transcendent
文章作者: Gavin Wang
文章链接: 手机整机测试 | Transcendent
本文章著作权归作者所有，任何形式的转载都请注明出处。