常见损失函数

机器学习中的所有算法都依赖于最小化或最大化一个函数，称之为目标函数，最小化的这组函数被称为损失函数。损失函数是衡量预测模型预测期望结果表现的指标。寻找函数最小值的最常用方法是梯度下降。

机器学习中的监督学习本质上是给定一系列训练样本$(x_i,y_i)$，尝试学习$x\to y$的映射关系，使得给定一个$x$，即使$x$不在训练样本中，也能够得到尽量接近真$y$的输出$\hat{y}$。而损失函数（Loss Function）是这个过程中关键的一个组成部分，用来衡量模型的输出$\hat{y}$与真实的$y$之间的差距，给模型的优化指明方向。

损失函数（Loss Function）、代价函数（Cost Function）和目标函数（Object Function）的区别联系。

• 损失函数（Loss Function） 通常是针对单个训练样本而言，给定一个模型输出$\hat{y}$与真实的$y$，损失函数输出一个实值损失$l=f(y_i,{\hat{y}}_i)$
• 代价函数（Cost Function） 通常是针对整个训练集（或者在使用mini-batch gradient descent时一个mini-batch）的总损失$J={\sum }_{i=1}^{N}f(y_i,{\hat{y}}_i)$
• 目标函数（Object Function） 是一个更通用的术语，表示任意希望被优化的函数。

说明：因为损失函数和代价函数只是在针对样本集上的区别，因此称呼时用损失函数，公式中实际上采用的是代价函数。

损失函数可以大致分为两类：分类损失（Classification Loss）和回归损失（Regression Loss）。

回归函数预测实数值，分类函数预测标签。

回归损失

均方差损失（Mean Squared Error Loss，MSE Loss/L2 Loss）

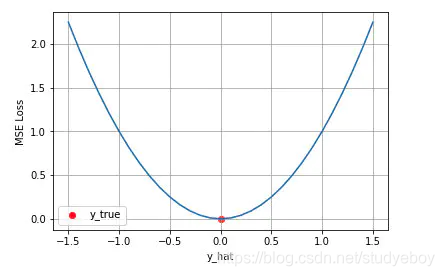
均方差 Mean Squared Error (MSE) 损失是机器学习、深度学习回归任务中最常用的一种损失函数，也称为 L2 Loss。其基本形式如下

随着预测与真实值的绝对误差的增加，均方差损失成二次方增加。

在一定的假设条件下，可以使用最大似然得到均方误差损失的形式。假设模型预测与真实值之间的误差服从标准高斯分布（$\mu =0,\sigma =1$），则给定一个$x_i$模型输出真实值$y_i$的概率为：

进一步假设数据集中N个样本点之间相互独立，则给定所有$x$输出所有真实值$y$的概率，即似然Likehood，为所有$p(y_i|x_i)$的累乘。

通常为了计算方便，使用最大化对数似然Log-Likehood。

去掉与${\hat{y}}_i$无关的第一项，然后转换为最小化负对数似然Negative Log-Likehood。

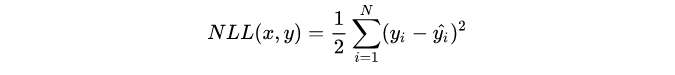
这个实际上就是均方误差损失的形式。即在模型输出与真实值的误差服从高斯分布的假设下，最小化均方差损失函数与极大似然估计本质上是一致的，因此在这个假设能被满足的场景中（比如回归），均方差损失是一个很好的损失函数选择；当这个假设没能被满足的场景中（比如分类），均方差损失不是一个好的选择。

平均绝对误差损失（Mean Absolute Error Loss，MAE Loss/L1 Loss）

平均绝对误差 Mean Absolute Error (MAE) 是另一类常用的损失函数，也称为 L1 Loss。其基本形式如下

随着预测与真实值绝对误差 $|y-\hat{y}|$ 的增加，MAE 损失呈线性增长

在一定的假设下通过最大似然得到MAE损失的形式，假设模型预测与真实值之间的误差服从拉普拉斯分布Laplace distribution（$\mu =0,b=1$），则给定一个$x_i$模型输出真实值$y_i$的概率为：

可以得到的负对数似然实际上就是MAE损失的形式：

MAE和MSE作为损失函数的主要区别是：

• MSE通常比MAE可以更快的收敛 当使用梯度下降算法时，MSE损失的梯度为$-{\hat{y}}_i$，而MAE损失的梯度为$\pm 1$，即MSE的梯度的scale会随着误差大小变化，而MAE的梯度的scale则一直保持为1，即便在绝对误差$|y_i-{\hat{y}}_i|$很小的时候MAE的梯度scale也同样为1，这实际上非常不利于模型的训练的。当然可以通过在训练过程中动态调整学习率缓解这个问题，但是总的来说，损失函数梯度之间的差异导致了MSE在大部分时候比MAE收敛的更快。这也是MSE更流行的原因。
  

• MAE对于outlier更加robust ，即不受outlier影响。

  • 从直观角度，MAE和MSE损失在同一图中，由于MAE损失与绝对误差之间是线性关系，MSE损失与误差是平方关系，当误差非常大的时候，MSE损失会远远大于MAE损失。因此当数据中出现一个误差非常大的outlier时，MSE会产生一个非常大的损失，对模型的训练会产生较大的影响。
    
  • 从两个损失函数的假设出发，MSE假设了误差服从高斯分布，MAE假设了误差服从拉普拉斯分布。拉普拉斯分布本身对于outlier更加robust。当右图右侧出现了outlier时，拉普拉斯分布相比高斯分布受到的影响要小很多。因此拉普拉斯分布为假设的MAE对outlier比高斯分布为假设的MSE更加robust。
    

平滑的平均绝对误差（Huber Loss/Smooth Mean Absolute Error Loss）

MSE 损失收敛快但容易受 outlier 影响，MAE 对 outlier 更加健壮但是收敛慢，Huber Loss 则是一种将 MSE 与 MAE 结合起来，取两者优点的损失函数，也被称作 Smooth Mean Absolute Error Loss 。其原理很简单，就是在误差接近 0 时使用 MSE，使损失函数可导并且梯度更加稳定；误差较大时使用 MAE，可以降低outlier的影响，使训练对outlier更加健壮。缺点是需要额外的设置一个$\delta$超参数。公式为

上式中$\delta$是 Huber Loss 的一个超参数，$\delta$的值是 MSE 和 MAE 两个损失连接的位置。上式等号右边第一项是 MSE 的部分，第二项是 MAE 部分，在 MAE 的部分公式为 $\delta |y_i-{\hat{y}}_i|-\frac{1}{2}{\delta }^2$是为了保证误差 $|y-\hat{y}|=\pm \delta$ 时 MAE 和 MSE 的取值一致，进而保证 Huber Loss 损失连续可导。

下图是$\delta =1.0$时的 Huber Loss，可以看到在 $[-\delta ,\delta ]$ 的区间内实际上就是 MSE 损失，在 $(-\infty ,\delta )$ 和 $(\delta ,\infty )$区间内为 MAE损失。

分位损失（Quantile Loss）

分位数回归 Quantile Regression 是一类在实际应用中非常有用的回归算法，通常的回归算法是拟合目标值的期望或者中位数，而分位数回归可以通过给定不同的分位点，拟合目标值的不同分位数。例如我们可以分别拟合出多个分位点，得到一个置信区间，如下图所示

分位数回归是通过使用分位数损失 Quantile Loss 来实现这一点的，分位数损失形式如下，式中的 r 分位数系数。

这个损失函数是一个分段的函数 ，将 ${\hat{y}}_i\ge y_i$（高估） 和 ${\hat{y}}_i<y_i$ （低估） 两种情况分开来，并分别给予不同的系数。当 $r>0.5$ 时，低估的损失要比高估的损失更大，反过来当 $r<0.5$时，高估的损失比低估的损失大；分位数损失实现了分别用不同的系数控制高估和低估的损失，进而实现分位数回归。特别地，当 $r=0.5$ 时，分位数损失退化为 MAE 损失，从这里可以看出 MAE 损失实际上是分位数损失的一个特例 — 中位数回归（这也可以解释为什么 MAE 损失对 outlier 更鲁棒：MSE 回归期望值，MAE 回归中位数，通常 outlier 对中位数的影响比对期望值的影响小）。

下图是取不同的分位点 0.2、0.5、0.6 得到的三个不同的分位损失函数的可视化，可以看到 0.2 和 0.6 在高估和低估两种情况下损失是不同的，而 0.5 实际上就是 MAE。

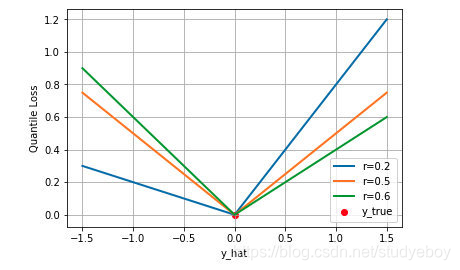
分类损失

MSE、MAE、Huber Loss和分位损失等损失函数都是适用于回归问题损失函数，对于分类问题，最常用的损失函数是交叉熵损失函数 Cross Entropy Loss。

交叉熵损失函数

二分类

考虑二分类，在二分类中我们通常使用 Sigmoid 函数将模型的输出压缩到 (0, 1) 区间内 ${\hat{y}}_i\in (0,1)$，用来代表给定输入$x_i$ ，模型判断为正类的概率。由于只有正负两类，因此同时也得到了负类的概率。

将两式子合并

假设数据点之间独立同分布，则似然可以表示为

对似然取对数，然后加负号变成最小化负对数似然，即为交叉熵损失函数的形式

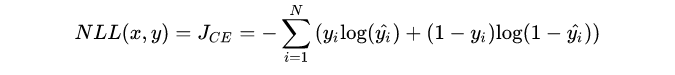
下图是对二分类的交叉熵损失函数的可视化，蓝线是目标值为 0 时输出不同输出的损失，黄线是目标值为 1 时的损失。可以看到越接近目标值损失越小，随着误差变差，损失呈指数增长。

多分类

在多分类的任务中，交叉熵损失函数的推导思路和二分类是一样的，变化的地方是真实值$y_i$现在是一个 One-hot 向量，同时模型输出的压缩由原来的 Sigmoid 函数换成 Softmax 函数。Softmax 函数将每个维度的输出范围都限定在 (0,1) 之间，同时所有维度的输出和为 1，用于表示一个概率分布。

其中 $k\in K$ 表示 K 个类别中的一类，同样的假设数据点之间独立同分布，可得到负对数似然为

由于 $y_i$ 是一个 one-hot 向量，除了目标类为 1 之外其他类别上的输出都为 0，因此上式也可以写为

其中 $c_i$ 是样本$x_i$的目标类。通常这个应用于多分类的交叉熵损失函数也被称为 Softmax Loss 或者 Categorical Cross Entropy Loss。

均方差损失假设了误差服从高斯分布，在分类任务下这个假设没办法被满足，因此效果会很差。为什么分类中用交叉熵损失，从最大似然的角度就是上面的推导，还可以用信息论来解释交叉熵损失。

假设对于样本 $x_i$ 存在一个最优分布 $y_i^{\star }$真实地表明了这个样本属于各个类别的概率，那么我们希望模型的输出 ${\hat{y}}_i$尽可能地逼近这个最优分布，在信息论中，我们可以使用 KL 散度 Kullback–Leibler Divergence 来衡量两个分布的相似性。给定分布 $p$和分布 $q$ ， 两者的 KL 散度公式如下

其中第一项为分布 $p$的信息熵，第二项为分布$p$和 $q$ 的交叉熵。将最优分布$y_i^{\star }$和输出分布 ${\hat{y}}_i$ 带入 $p$和 $q$ 得到

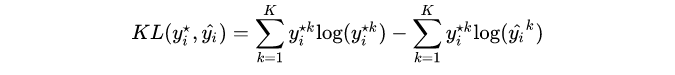
由于我们希望两个分布尽量相近，因此我们最小化 KL 散度。同时由于上式第一项信息熵仅与最优分布本身相关，因此我们在最小化的过程中可以忽略掉，变成最小化

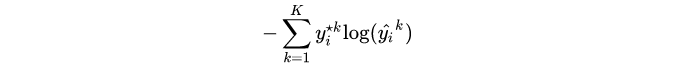
我们并不知道最优分布$y_i^{\star }$ ，但训练数据里面的目标值 $y_i$ 可以看做是$y_i^{\star }$的一个近似分布

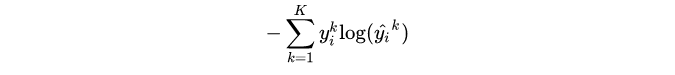
这个是针对单个训练样本的损失函数，如果考虑整个数据集，则

可以看到通过最小化交叉熵的角度推导出来的结果和使用最大 化似然得到的结果是一致的。

合页损失（Hinge Loss）

合页损失 Hinge Loss 是另外一种二分类损失函数，适用于 maximum-margin 的分类，支持向量机 Support Vector Machine (SVM) 模型的损失函数本质上就是 Hinge Loss + L2 正则化。合页损失的公式如下

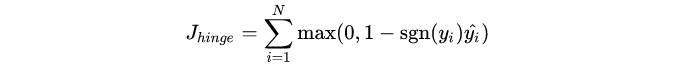
下图是 $y$ 为正类， 即 $sgn(y)=1$ 时，不同输出的合页损失示意图

可以看到当 $y$ 为正类时，模型输出负值会有较大的惩罚，当模型输出为正值且在 (0,1)区间时还会有一个较小的惩罚。即合页损失不仅惩罚预测错的，并且对于预测对了但是置信度不高的也会给一个惩罚，只有置信度高的才会有零损失。使用合页损失直觉上理解是要找到一个决策边界，使得所有数据点被这个边界正确地、高置信地被分类。

参考资料
机器学习常用损失函数小结
常见的损失函数
如何选择合适的损失函数，请看…