本文目录:
一、损失函数概念
在深度学习中, 损失函数是用来衡量模型参数质量的函数, 衡量的方式是比较网络输出(预测值)和真实输出(真实值)的差异。
模型通过最小化损失函数的值来调整参数,使其输出更接近真实值。
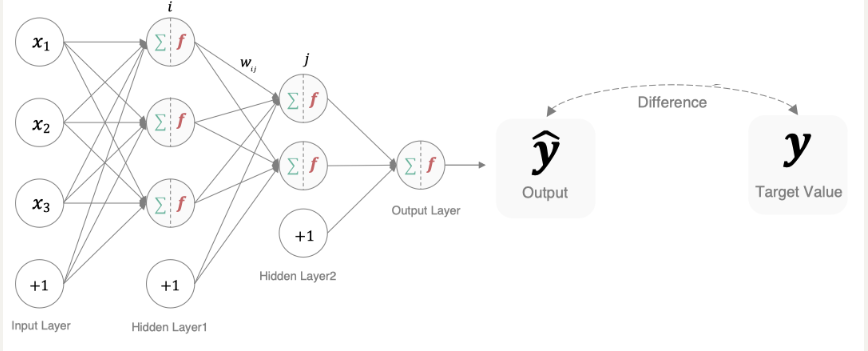
损失函数作用:**
- 评估性能:反映模型预测结果与目标值的匹配程度。
- 指导优化:通过梯度下降等算法最小化损失函数,优化模型参数。
二、分类任务损失函数
在深度学习的分类任务中使用最多的是交叉熵损失函数,所以在这里我们着重介绍这种损失函数。
(一)二分类任务损失函数
在处理二分类任务(如判断图像是否为猫、垃圾邮件检测等)时,我们使用sigmoid激活函数和二分类的交叉熵损失函数,计算公示如下(类似伯努利概率计算):
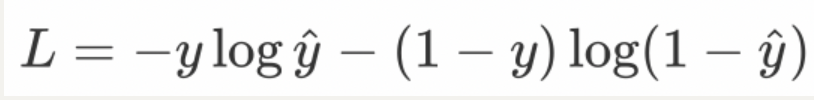
其中:
-
y:真实标签(0 或 1);
-
^y: 模型的预测概率(通常由 Sigmoid 函数输出,范围 ∈(0,1));
-
L:单个样本的损失值(所有样本的损失通常取平均)。
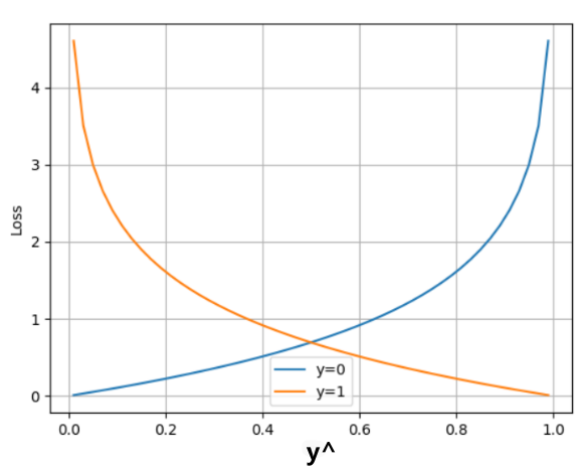
如上图所示:

在PyTorch中实现时使用nn.BCELoss() 实现,如下所示:
import torch
from torch import nn
def test02():
# 1 设置真实值和预测值
y_true = torch.tensor([0, 1, 0], dtype=torch.float32)
# 预测值是sigmoid输出的结果
y_pred = torch.tensor([0.6901, 0.5459, 0.2469], requires_grad=True)
# 2 实例化二分类交叉熵损失
loss = nn.BCELoss()
# 3 计算损失
my_loss = loss(y_pred, y_true).detach().numpy()
print('loss:', my_loss)
(二)多分类任务损失函数
在多分类任务通常使用softmax将logits(输出值)转换为概率的形式,所以多分类的交叉熵损失也叫做softmax损失(重要),它的计算方法是:
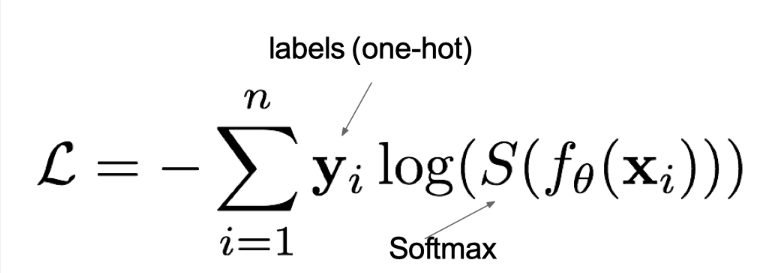
其中:
- yi:样本的真实标签(one-hot编码,如 [0, 0, 1, 0]);
- 神经网络的原始输出(未归一化的 logits);
- S是softmax激活函数,将 logits 转换为概率分布;
- L用来衡量真实值y和预测值f(x)之间差异性的损失结果(越小表示预测越准确)。

关于多分类交叉熵损失计算:
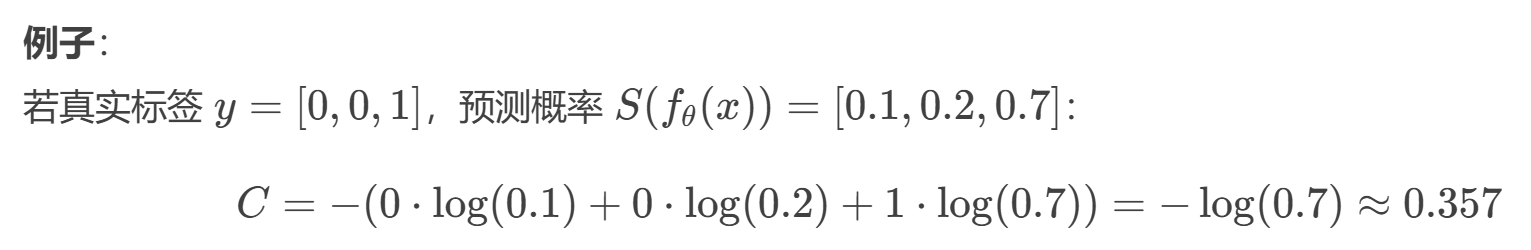
从概率角度理解,我们的目的是最小化正确类别所对应的预测概率的对数的负值(损失值最小),如下图所示:
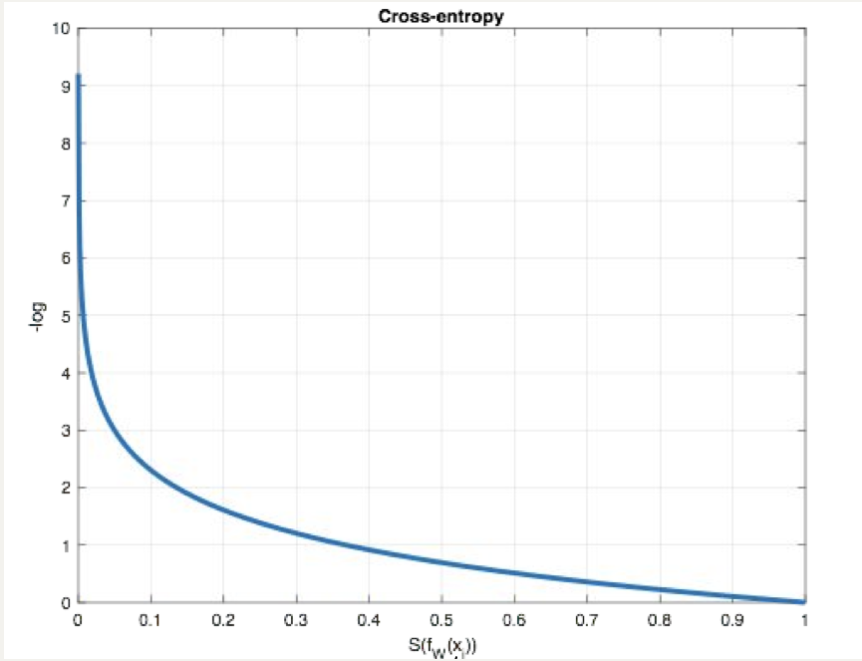
如上图所示:

在PyTorch中使用nn.CrossEntropyLoss()实现,如下所示:
import torch
from torch import nn
# 分类损失函数:交叉熵损失使用nn.CrossEntropyLoss()实现。nn.CrossEntropyLoss()=softmax+损失计算
def test01():
# 设置真实值:既可以是热编码后的结果,也可以是没进行热编码的真实值
# y_true = torch.tensor([[0, 1, 0], [0, 0, 1]], dtype=torch.float32)
# 注意:类型必须是64位整型数据
y_true = torch.tensor([1, 2], dtype=torch.int64)
y_pred = torch.tensor([[0.2, 0.6, 0.2], [0.1, 0.8, 0.1]], requires_grad=True, dtype=torch.float32)
# 实例化交叉熵损失,默认求平均损失
# reduction='sum':总损失
loss = nn.CrossEntropyLoss()
# 计算损失结果
my_loss = loss(y_pred, y_true).detach().numpy()
print('loss:', my_loss)
(三)二分类交叉熵VS多分类交叉熵
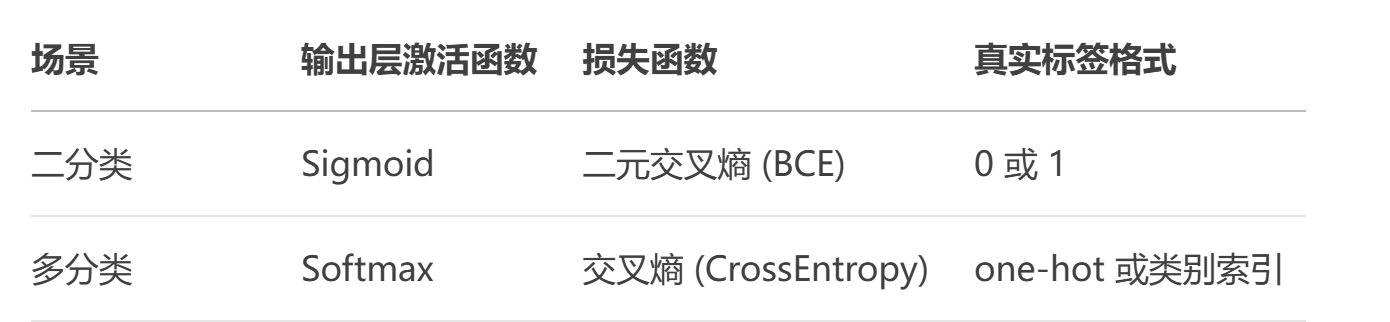
三、回归任务损失函数
(一)MAE损失函数
**mean absolute loss(MAE)**也被称为L1 Loss,是以绝对误差作为距离
损失函数公式:
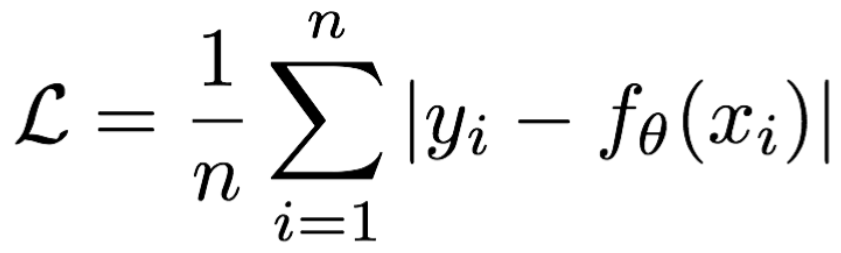
图像如下图所示:
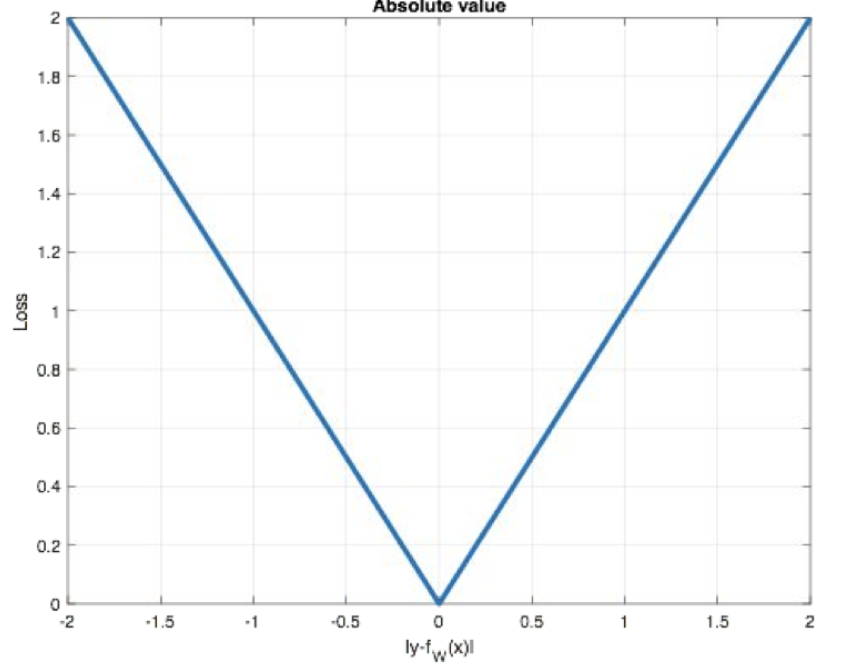
特点:
- 由于L1 loss具有稀疏性,为了惩罚较大的值,因此常常将其作为正则项添加到其他loss中作为约束。(0点不可导, 产生稀疏矩阵);
- L1 loss的最大问题是梯度在零点不平滑,导致会跳过极小值;
- 适用于回归问题中存在异常值或噪声数据时,可以减少对离群点的敏感性。
在PyTorch中使用nn.L1Loss()实现,如下所示:
import torch
from torch import nn
# 计算inputs与target之差的绝对值
def test03():
# 1 设置真实值和预测值
y_pred = torch.tensor([1.0, 1.0, 1.9], requires_grad=True)
y_true = torch.tensor([2.0, 2.0, 2.0], dtype=torch.float32)
# 2 实例MAE损失对象
loss = nn.L1Loss()
# 3 计算损失
my_loss = loss(y_pred, y_true).detach().numpy()
print('loss:', my_loss)
(二)MSE损失函数
**Mean Squared Loss/ Quadratic Loss(MSE loss)**也被称为L2 loss,或欧氏距离,它以误差的平方和的均值作为距离
损失函数公式:
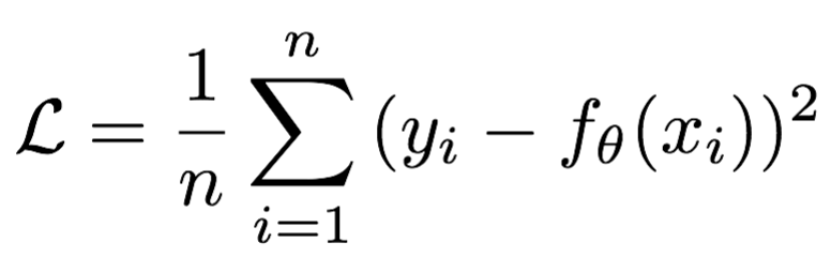
曲线如下图所示:
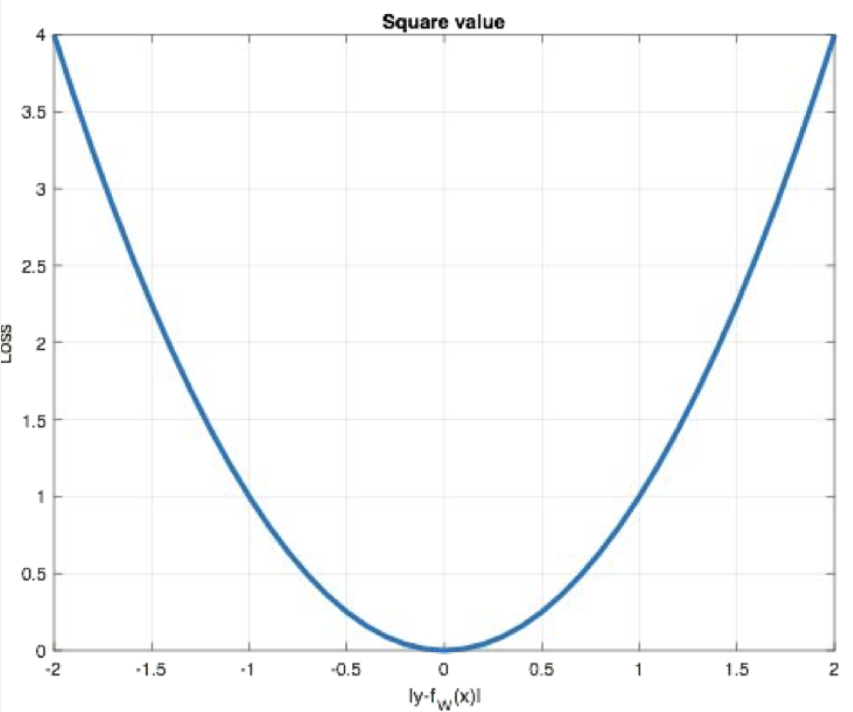
特点:
-
L2 loss也常常作为正则项,对于离群点(outliers)敏感,因为平方项会放大大误差;
-
当预测值与目标值相差很大时, 梯度容易爆炸;
- 梯度爆炸:指在反向传播过程中,梯度值急剧增大(甚至变成NaN或inf),导致模型参数剧烈更新,最终无法收敛。
-
适用于大多数标准回归问题,如房价预测、温度预测等。
在PyTorch中通过nn.MSELoss()实现:
import torch
from torch import nn
def test04():
# 1 设置真实值和预测值
y_pred = torch.tensor([1.0, 1.0, 1.9], requires_grad=True)
y_true = torch.tensor([2.0, 2.0, 2.0], dtype=torch.float32)
# 2 实例MSE损失对象
loss = nn.MSELoss()
# 3 计算损失
my_loss = loss(y_pred, y_true).detach().numpy()
print('myloss:', my_loss)
(三) Smooth L1损失函数
smooth L1说的是光滑之后的L1,是一种结合了均方误差(MSE)和平均绝对误差(MAE)优点的损失函数。它在误差较小时表现得像 MSE,在误差较大时则更像 MAE。
Smooth L1损失函数如下式所示:
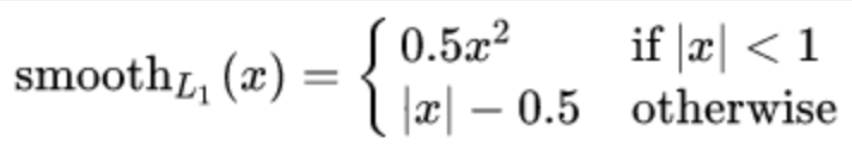
其中:𝑥=f(x)−y 为真实值和预测值的差值。
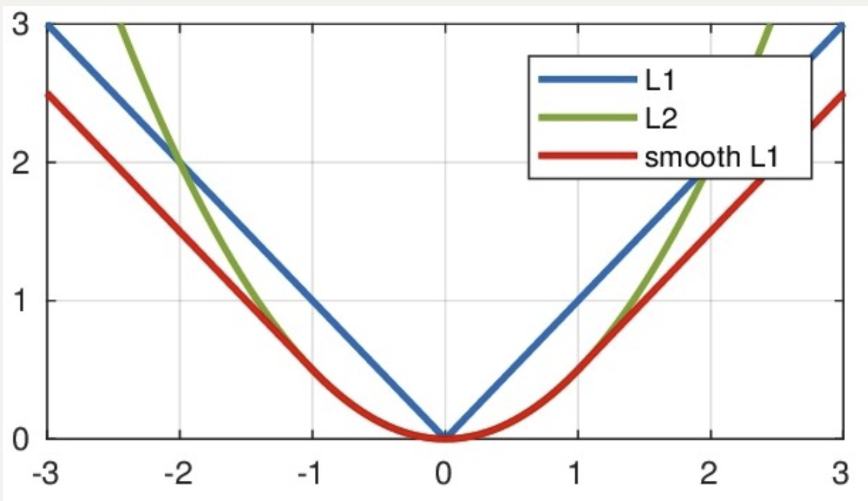
从上图中可以看出,smooth L1函数实际上就是一个分段函数:
- 在[-1,1]之间实际上就是L2损失,这样解决了L1的不光滑问题
- 在[-1,1]区间外,实际上就是L1损失,这样就解决了离群点梯度爆炸的问题.
特点:
-
对离群点更加鲁棒(鲁棒性指模型在输入数据存在噪声、异常值或分布偏移时,仍能保持稳定预测性能的能力):当误差较大时,损失函数会线性增加(而不是像MSE那样平方增加),因此它对离群点的惩罚更小,避免了MSE对离群点过度敏感的问题;
-
计算梯度时更加平滑:与MAE相比,Smooth L1在小误差时表现得像MSE,避免了在训练过程中因使用绝对误差而导致的梯度不连续问题(影响模型的收敛性和稳定性)。
在PyTorch中使用nn.SmoothL1Loss()计算该损失,如下所示:
import torch
from torch import nn
def test05():
# 1 设置真实值和预测值
y_true = torch.tensor([0, 3])
y_pred = torch.tensor([0.6, 0.4], requires_grad=True)
# 2 实例smmothL1损失对象
loss = nn.SmoothL1Loss()
# 3 计算损失
my_loss = loss(y_pred, y_true).detach().numpy()
print('loss:', my_loss)
附赠:
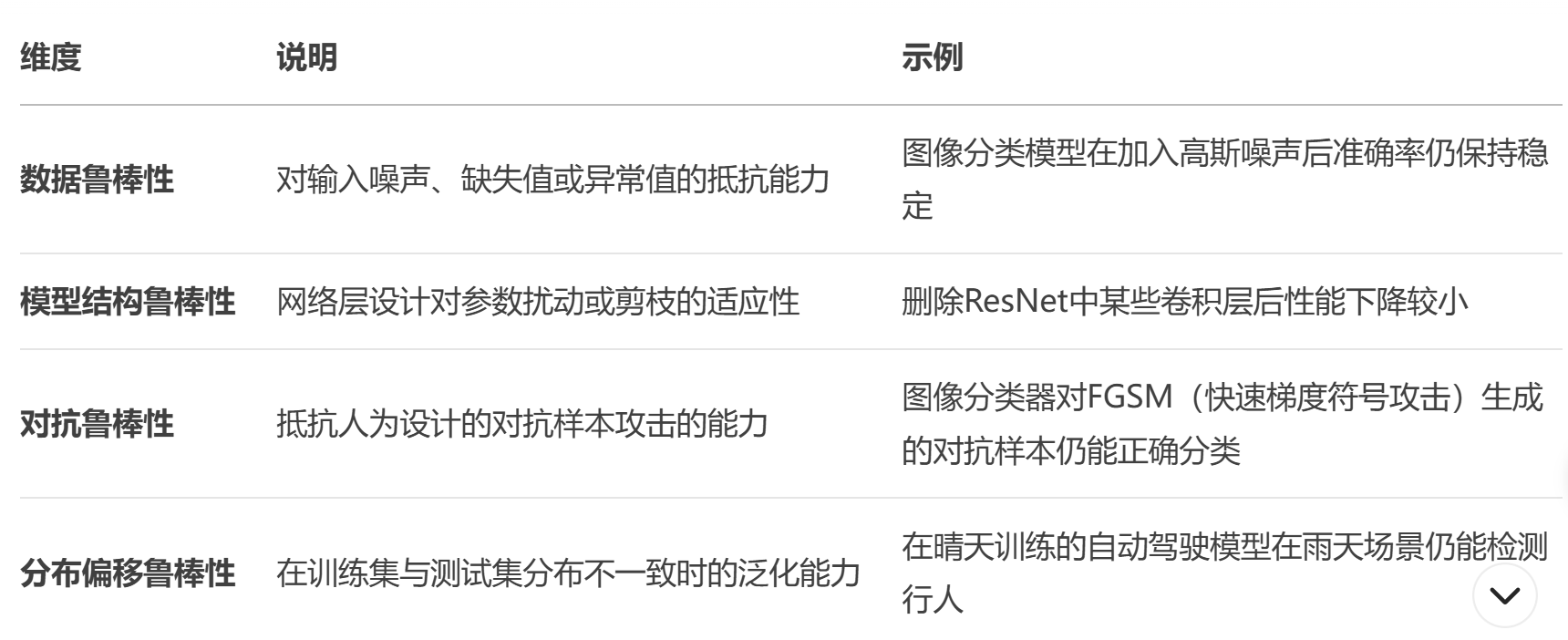
1.鲁棒性的核心维度
2.梯度不连续的具体表现

3.梯度爆炸VS梯度消失

今天的分享到此结束,欢迎相互学习。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








