动态规划算法

前言

最近帮同学写一个程序，给出100多个金额，用数组表示为money[1-100]，再给出一个数额SUM。如果money数组里面有哪几项之和等于SUM，那么这几项就是符合条件的一个组合。现在需要做的是，找出所有符合要求的组合。

举一个简单的例子，假设money为{1,1,2,3,4}，和为6的所有组合为1+1+4, 1+2+3，1+2+3，2+4。

对于我同学给的这个程序要求，不算不知道，一算吓一跳，100个数的所有组合情况是2的100次方，是天文数字了。（本机测试2的32次方次数的浮点运算消耗30秒左右时间）

所以没有办法罗列出所有的组合，而且在维基百科上查找NPC问题(Non-deterministic Polynomial complete problem非确定多项式完备问题）时，第一个例子就是这种子集合加总问题（说白一点就是组合之和）。维基百科上提到：“这个问题的答案非常容易验证，但目前没有任何一个够快的方法可以在合理的时间内（意即多项式时间）找到答案。只能一个个将它的子集取出来一一测试，它的时间复杂度是Ο（2ⁿ），n是此集合的元素数量。”

当然，不能因为罗列所有的组合是不可行的，就不写这个程序了吧，代码是死的，人是活的。可以制定策略嘛，比如说如果一个组合里面最多只能有5项；尝试遍历组合的时候，只要找到了10种或者20种组合，后面的就不再计算了。而对于实在搜索不到的组合，我们可以采用超时的方式，比如计算30秒或1分钟之后就不再计算了，而是返回没有找到可行的组合。

说了这么多，好像和我写的标题还没有什么联系，其实是这样的，一开始我是采用回溯法去解决上面的问题的，但是我一直在想是不是可以用背包算法或者动态规划的算法来写这个程序（当然最后得到的结论是不可行）。

因为以前看过动态规划方面的一些资料，现在又忘的差不多了，所以想回头看一下，顺便学习一下。= =

这里有一篇很不错的讲动态规划的文章：http://hawstein.com/posts/dp-novice-to-advanced.html，里面通过实例由浅入深的讲解了动态规划的使用。下面我举一下里面的两个例子。

第一个例子 需要的最少硬币数：

如果我们有面值为1元、4元和5元的硬币若干枚，如何用最少的硬币凑够12元（12可替换为任意的N>0）？

注意：在这里贪心算法获得的结果不是最优的，如果按照每次都优先选最大面值的，那么会先拿两次5元得到10元，剩下的两元再拿两个1元的，总共需要4枚硬币。而更优化的方案是拿3枚4元的硬币。

下面我们就来看看该如何解决这个问题。

根据已经有的硬币面值，我们知道最后一次可以选择的硬币有3种方案（1元，4元和5元），如果最后一次是选择1元硬币凑够12元的，那么倒数第二步就应该是凑够了12-1= 11元。同理，如果最后一次是选择4元凑够12元的，则倒数第二步就应该是凑够了12-4 = 8元，如果最后一次是选择5元而凑够12元的，则倒数第二步就应该是凑够了12-5 = 7元。

换句话说：只有3种状态能够通过只取一枚硬币就凑够12元，分别是11元、8元、7元。现在假设凑够11元、8元、7元所需要的最少硬币数量是x、y、z，那么凑够12元所需要的最少硬币数量就是x,y,z里面的最小值 + 1。用表达式表示就是min(x,y,z)+1，从递归的角度来看问题就被递归下降分解了，从原来的求凑够12元需要的最少硬币数转换成了求凑够11元、8元、7元所需要的最少硬币数。那么把这种递归下降分解的思路继续拓展下去，最终会终止到1元硬币的情况。

我们用N(i)表示凑够i元需要的最少硬币数量。那么N(12) = min ( N(11), N(8), N(7) ) + 1. 转换成更一般的公式就是N(i) = min ( N(i-1), N(i-4), N(i-5) ) + 1.根据这个公式我们可以写出递归函数，代码如下：

int GetMinCoinCount(int nSum)
{
    if (1 == nSum || 4 == nSum || 5 == nSum)
    {
        return 1;
    }
    if (nSum > 5)
    {
        return MIN_THREE(GetMinCoinCount(nSum-1), GetMinCoinCount(nSum-4), GetMinCoinCount(nSum-5))+1;
    }
    else if (nSum > 4)
    {
        return MIN_TWO(GetMinCoinCount(nSum-1), GetMinCoinCount(nSum-4))+1;
    }
    else
    {
        return GetMinCoinCount(nSum-1)+1;
    }
}

递归虽然代码写起来很简单，理解起来也不困难，但是效率非常低，究其原因就是因为我们重复计算了太多中间值，比如用上面的代码计算凑够12元所需要的最少硬币数，上面的这个函数被调用了2620次之多（在函数内部加一个静态变量或全局变量，进行递增计算即可）。

当需要凑够27元时，GetMinCoinCount函数被调用次数已经达到29,1208,9123次（29亿）。消耗的时间在几十秒的数量级。下面是测试代码和测试结果。

for (int m = 12; m < 30; m++)
    {
        g_i = 0;
        int n = GetMinCoinCount(m);
        printf("计算凑成%d元最少需要的硬币数量,调用GetMinCoinCount函数0x%08X次。\r\n", m, g_i);
    }

计算凑成12元最少需要的硬币数量,调用GetMinCoinCount函数0x00000A3C次。
计算凑成13元最少需要的硬币数量,调用GetMinCoinCount函数0x0000184B次。
计算凑成14元最少需要的硬币数量,调用GetMinCoinCount函数0x00003535次。
计算凑成15元最少需要的硬币数量,调用GetMinCoinCount函数0x00003F7A次。
计算凑成16元最少需要的硬币数量,调用GetMinCoinCount函数0x00011692次。
计算凑成17元最少需要的硬币数量,调用GetMinCoinCount函数0x0004951B次。
计算凑成18元最少需要的硬币数量,调用GetMinCoinCount函数0x000A1756次。
计算凑成19元最少需要的硬币数量,调用GetMinCoinCount函数0x001561CA次。
计算凑成20元最少需要的硬币数量,调用GetMinCoinCount函数0x00180DE3次。
计算凑成21元最少需要的硬币数量,调用GetMinCoinCount函数0x006A7855次。
计算凑成22元最少需要的硬币数量,调用GetMinCoinCount函数0x01C2A51C次。
计算凑成23元最少需要的硬币数量,调用GetMinCoinCount函数0x03E4E8B7次。
计算凑成24元最少需要的硬币数量,调用GetMinCoinCount函数0x083F6AC5次。
计算凑成25元最少需要的硬币数量,调用GetMinCoinCount函数0x09447736次。
计算凑成26元最少需要的硬币数量,调用GetMinCoinCount函数0x29019F66次。
计算凑成27元最少需要的硬币数量,调用GetMinCoinCount函数0xAD92F423次。

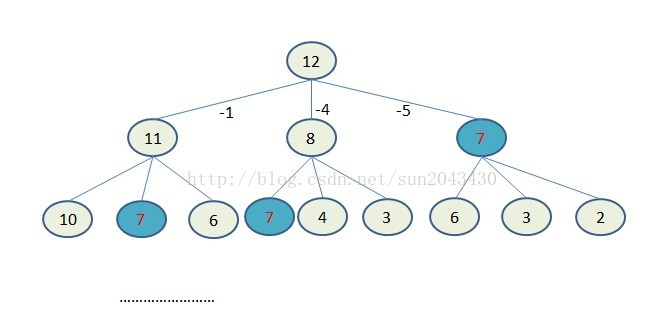
显然，这样的递归算法是不可取的。我们分析一下问题的原因，就是因为同一个数值在递归函数中进行了多次计算，比如我们仍然以凑够12元为例，下图可以形象地展示计算过程：

由此图我们可以看出，存在大量的重复计算。比如图中的7。整个树上的节点增长速度是指数级的，树的最大深度为12层。每个节点的孩子节点为0到3个不等。

如果我们能够消除重复计算，将大大提升计算的速度。我们可以将计算出来的中间值保存起来，等下一次需要时直接拿来用，而不是又重新去计算一遍。

那么中间状态有多少种情况呢？对于凑成12元来说，所有可能需要用到的中间状态也就是从1元到11元。所以我们用一个数组来表示，代码修改如下。

int g_nMinArray[100] = {};
int g_i = 0;
int GetMinCoinCount2(int nSum)
{
    g_i++;
    if (0 != g_nMinArray[nSum])
    {
        return g_nMinArray[nSum];
    }
    if (1 == nSum || 4 == nSum || 5 == nSum)
    {
        g_nMinArray[nSum] = 1;
        return 1;
    }
    if (nSum > 5)
    {
        g_nMinArray[nSum] = MIN_THREE(GetMinCoinCount2(nSum-1), GetMinCoinCount2(nSum-4), GetMinCoinCount2(nSum-5))+1;
    }
    else if (nSum > 4)
    {
        g_nMinArray[nSum] = MIN_TWO(GetMinCoinCount2(nSum-1), GetMinCoinCount2(nSum-4))+1;
    }
    else
    {
        g_nMinArray[nSum] = GetMinCoinCount2(nSum-1)+1;
    }
    return g_nMinArray[nSum];
}

相应的测试代码如下：

    for (int m = 12; m <= 100; m++)
    {
        g_i = 0;
        memset(g_nMinArray, 0, sizeof(g_nMinArray));
        int n = GetMinCoinCount2(m);
        printf("计算凑成%d元最少需要的硬币数量,调用GetMinCoinCount2函数%d次。\r\n", m, g_i);
        printf("%d\r\n", n);
    }

打印输出的部分结果：

计算凑成94元最少需要的硬币数量,调用GetMinCoinCount2函数626次。
19
计算凑成95元最少需要的硬币数量,调用GetMinCoinCount2函数633次。
19
计算凑成96元最少需要的硬币数量,调用GetMinCoinCount2函数640次。
20
计算凑成97元最少需要的硬币数量,调用GetMinCoinCount2函数647次。
20
计算凑成98元最少需要的硬币数量,调用GetMinCoinCount2函数654次。
20
计算凑成99元最少需要的硬币数量,调用GetMinCoinCount2函数661次。
20
计算凑成100元最少需要的硬币数量,调用GetMinCoinCount2函数668次。
20

可以看出，通过保存中间状态的方式，我们将指数级的计算时间缩短到了线性级。

另外，我们上面的思路一直是递归的思路，通过将递归改成递推，我们可以减少不必要的函数调用和栈空间开销，进一步提高计算速度。相应代码如下：

int GetMinCoin(int nSum)
{
    for (int i = 1; i <= nSum; i++)
    {
        if (1 == i || 4 == i || 5 == i)
        {
            g_nMinArray[i] = 1;
        }
        else if (i > 5)
        {
            g_nMinArray[i] = MIN_THREE(g_nMinArray[i-1], g_nMinArray[i-4], g_nMinArray[i-5])+1;
        }
        else if (i > 4)
        {
            g_nMinArray[i] = MIN_TWO(g_nMinArray[i-1], g_nMinArray[i-4])+1;
        }
        else
        {
            g_nMinArray[i] = g_nMinArray[i-1]+1;
        }
    }
    return g_nMinArray[nSum];
}

可以用这段代码的运行结果和上面递归代码的计算结果进行比较验证。这个例子就先讲到这里了，其实和斐波那契数列的求法在思想上挺类似（维基百科中文版的动态规划词条下就是用斐波那契数列来做例子的）。

在这里有一个很重要的思想就是保存中间子过程供多次使用，用空间换时间加快算法计算时间，这是动态规划算法的精髓。

第二个例子 路径经过的最大值（最小值）：

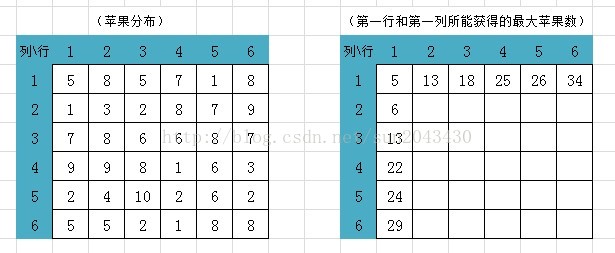
原题：平面上有N*M个格子，每个格子中放着一定数量的苹果。从左上角的格子开始，每一步只能向下走或是向右走，每次走到一个格子就把格子里的苹果收集起来， 这样一直走到右下角，问最多能收集到多少个苹果。

不妨用一个表格来表示：

    {5, 8, 5, 7, 1, 8},
    {1, 3, 2, 8, 7, 9},
    {7, 8, 6, 6, 8, 7},
    {9, 9, 8, 1, 6, 3},
    {2, 4,10, 2, 6, 2},
    {5, 5, 2, 1, 8, 8},

在这个6X6的表格里面填写了一些数表示所在格子中的苹果数量。根据题目的规则"每一步只能向下走或是向右走"，如果用i表示纵向，用j表示横向，那么能够到达a[i][j]处的只有两个位置a[i-1][j](上一格)和a[i][j-1]（左边一格），所以必然是取这两个位置中比较大的那一个点。依此回溯到a[0][0]，或者从a[0][0]递推到a[i][j]。

......... , ......... , a[i-1][j]

......... , a[[i][j-1], a[i][j] ,

基于这一点，我们可以从左上角开始将到达第一行和第一列中各点所能收集到的最大苹果数量填成一张表格。如下：

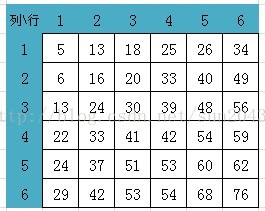
接下来填第2行，首先是第2行第2列的值，应该填写为 MAX（A[1][2], A[2][1]）+ A[2][2]对应的苹果数量。也就是说到达第2行第2列能获得的最大苹果数，要看第2行第1列所获得的苹果数（6）和第1行第2列所获得的苹果数（13），这两者哪个更大，谁大就取谁的值，显然第1行第2列所获得的苹果数（13）更大，所以用13加上第2行第2列的苹果数3 = 16，就是到达第2行第2列能获得的最大苹果数。同理，填所在格能获得的最大苹果数就是看它左面一格和上面一格哪个值更大，就取哪个值再加上自己格子里面的苹果数，就是到达此格能获得的最大苹果数。依此填完所有格子，最后得到下图：

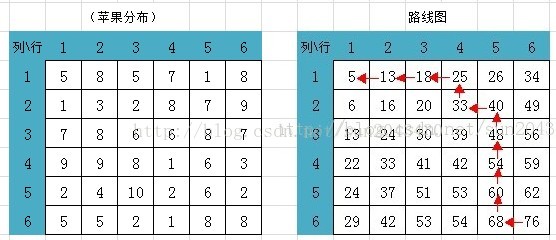
所以：到达右下角能够获得的最大苹果数量是76。所经过的路径可以通过倒推的方法得到，从右下角开始看所在格子的左边一格和上面一格哪边大就往哪边走，如果遇到一样大的，任选一条即可。

这样我们可以画出路线图，如下图右边表格：

这个例子的分析和解决方法大概就是这样了。在前面第一个例子里面我们提到：空间换时间是动态规划的精髓。但是一个问题是否能够用动态规划算法来解决，需要看这个问题是否能被分解为更小的问题（子问题）。而子问题之间是否有包含的关系，是区别动态规划算法和分治法的所在。一般来说，分治法的各个子问题之间是相互独立的，比如折半查找（二分查找）、归并排序等。而动态规划算法的子问题在往下细分为更小的子问题时往往会遇到重复的子问题，我们只处理同一个子问题一次，将子问题的结果保存下来，这就是动态规划的最大特点。

动态规划算法总结起来就是两点：

1 寻找递推（递归）关系，比较专业的说法叫做状态转移方程。

2 保存中间状态，空间换时间。

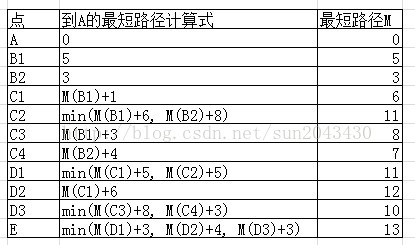
例子3：最短路径

现有一张地图，各结点代表城市，两结点间连线代表道路，线上数字表示城市间的距离。如图1所示，试找出从结点A到结点E的最短距离。

题目来源（http://blog.csdn.net/tiantangrenjian/article/details/6744484）

通过我们在例1和例2中的分析，首先是找到递归、递推关系。由图可知，要到达E点，能直接走到E的点是D1，D2，D3，所以和例1的思路一样，我们定义从A到某一点i的最短路径为M(i)，则M(E) = min(M(D1)+3, M(D2)+4, M(D3)+3)。而能够直接到达D1的点有C1，C2，能够到达D2的点有C1，能够到达D3的点有C3，C4。所以这也是一个递归的过程。当我们采用动态规划算法时，我们倒过来从A开始递推，A能够直接到达的点是B1，B2，所以M(B1) = 5， M(B2) = 3，接下来看C这一层，M(C1)= M(B1)+1 = 6,M(C2)= min(M(B1)+6, M(B2)+8) = min(5+6, 3+8) = 11。

全部计算出来的表格如下：

所以可得从A到E的最短路径长度为13。路线为A-B2-C4-D3-E。

例子4：LCS（最长公共子序列）

这个题目在网上非常多，一开始我不是很明白题目的意思，而且不知道求这个有什么实际意义。后来看了不少相关的文章，才明白了一些。

比如说有两个序列，序列A为{a,b,c,d,e,f,g}，序列B为{b,a,b,g,e,k,f},那么序列A和B的最长公共子序列是{a,b,e,f}。也就是说子序列不要求是连续的，只要前后顺序是对的就OK。

至于求最长公共子序列有什么实际意义呢？我举一个例子，你想比较两个文本的差异，A文本内容是“我打算明日去广州”，B文本内容是“我打算大后天去广州”，对于这样简单的文本，我们可以很容易地看出来差别在于A文本中的“明日”和B文本中的“大后天”，其他部分都是相同的。而如果我们只是简单的从头到尾一个字符一个字符去比较的话，其结果是只有前3个字符相同，后面的字符都不相同了。

而我们如果换成求最长公共子序列，那么“我打算去广州”是最长公共子序列，可以找到两个序列最大匹配的部分。而不匹配的部分就是真正有差异的地方。这就是求最长公共子序列的实际意义！

另外告诉大家一个秘密：软件开发中用于管理代码的SVN软件和GIT软件在判断你对代码进行了哪些位置的改动，也是需要求LCS的。^_^

而解决LCS的思路和第2个例子中的找走过的路径中获得苹果数最多的路径方法是一样的。建立一个2维数组（记为N），先初始化为全0，然后取两个数组中对应下标的元素依次进行比较，根据比较结果填满整个二维数组。我们首先来看看填完第一行和第一列的2维数组。

我们将序列A横向排列，序列B竖向排列，先来看第一行，N[0][0]位置填的是0，因为(A[0] == a) != (B[0] == b)。接下来看A[1] == B[0] == b，所以N[0][1]位置 = 1，那么再往后的N[0][2]一直到N[0][6]都应该填1，意思是用字符串"ab"、"abc"、"abcd","abcde","abcdef"、"abcdefg"和字符串"b"进行求最长公共子序列的操作得到的值都是1(也就是A[1] == B[0] == b)。

第一行处理完了我们同理可以填写出第一列的数值，首先N[0][0]已经处理过了，接下来看N[1][0]，因为A[0] == B[1] == a，所以数组的[1][0]处应该填1，然后整个第一列的后面位置都应该填为1，原因和分析第一行的时候一样。处理完成后的表格就是上图所示。这里和例子2有一点不同的地方是数组中填写的数值不能超过2维数组比较小的那个下标的值+1，因为数组N[i][j]表示的是序列A[0到j]和序列B[0到i]两个序列的最长公共子序列的长度，子序列的长度不可能超过给定的两个序列中长度较小的那个，最大也就是等于较短的序列的长度，也就是min(i,j)+1。

填完第一行和第一列后，我们再来看第二行第二列的位置N[1][1]处该填什么数值。首先，如果A[1]==B[1]那么这里应该填写为N[0][0]+1。

如果A[1]!=B[1]，这里应该填写N[1][0]和N[0][1]中较大的那个。至于原因，分析如下。

因为A[1]!=B[1]，所以得到的最长公共子序列中，最多也就是到A[1]，或者是到B[1]。假设最长公共子序列到达了A[1]，那么N[1][1]应该和N[0][1]相同。如果最长公共子序列达到的是B[1]，那么N[1][1]应该和N[1][0]相同。所以在A[1]!=B[1]情况下，N[1][1]的值是N[0][1]和N[1][0]这两个数值中的一个。因为是求最长的，所以我们当然选取较大的那一个。这一点和例2中的看左边一格和上边一格哪个数值大就取哪个类似。

根据上面的分析，我们将2维表格填写完整，如下图：

最后在二维表格中，N[6][6] = 4。所以最长公共子序列的长度为4。要知道最长公共子序列是什么，和例2中类似，从N[6][6]倒推到N[0][0]。首先在N[6][6]位置看A[6]和B[6]是否相同，结果是不相同，所以下一个要看的位置是N[6][5]和N[5][6]中值较大的那一个。也就是N[6][5]。在N[6][5]处，A[5]==B[6]==f，所以"f"是最长公共子序列里面的一个字符。因为A[5]==B[6]所以接下来看N[5][4]（左斜上方），A[4]和B[5]不等，所以要看N[5][4]左边一格和上边一格哪个格子的数值更大。这样就来到了N[4][4]。发现A[4]==B[4]==e，所以"e"也是最长公共子序列里面的一个字符。就这样按照：

1 遇到A序列和B序列里面字符相同的，那么这个字符是最长公共子序列里面的一个字符，下一个位置看左斜上方的格子。

2 遇到A序列和B序列里面字符不同的，就看左边一格和上边一格哪个数值更大，往值较大的格子走（相同的取其一，或者都尝试，看需求）。

最后走到数值为0的格子，得到最长公共子序列。当然，在这个过程中可能会遇到左边一格和上边一格数值相同的情况，那么此时我们可能会遇到2个一样长的最长公共子序列。

我们把上面的倒推过程用图形表示如下：

图中黄色的位置是A序列和B序列相应下标处字符相同的点，连起来是"abef"，这就是序列A和B的最长公共子序列。

当然细心的读者可能会发现在N[3][3]处，我们选择了向左走，没有选择向上走，其实如果要找到所有的最长公共子序列是应该在两边都可以走的时候都走一次的，这里我为了图面的整洁没有画这一条路线，且往上走最终也是会走到N[2][1]处，最后得到的最长公共子序列还是"abef"。

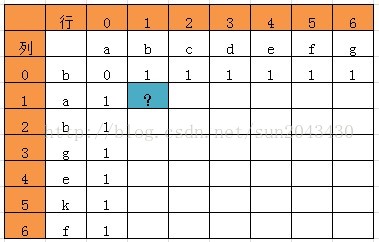
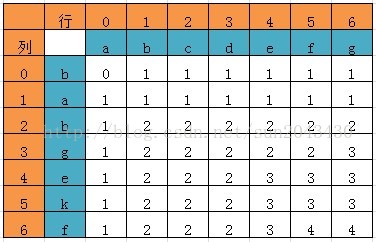
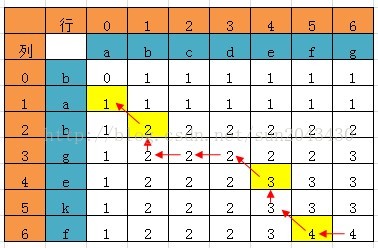
一些题外话：动态规划算法和人生

当我在学习第2个例子的时候，突然觉得动态规划算法和我们人生的决策很相似。

1. 两者都不喜欢走回头路，对于人生来说是走不了回头路，而对于算法来说回头路意味着做无用功，白白浪费时间。

2. 有时候，你并不知道以后的际遇是怎样的，只能在现阶段的情况下选择最优、最有发展前景的道路。但是当前最优的并不一定会带来整体的最优，比如例1里面我们不能简单的取最大面值的硬币。而在例2中，我们也不能只看到整个方格中最大的10（在第5行第3列）就不顾一切的朝着这个点奔过去。^_^

3. 个人的力量在强也强不过集体，优秀的团队才能获得最大的价值。（说的还是例2那个悲催的全场最大的10=.=）

好了，不多扯了。