数据结构之二叉树 python实现

二叉树

1. 概念及主要性质

二叉树¹是一种最简单的树形结构。其特点是每个节点至多关联到两个后继节点。后继节点分为左关联节点和右关联节点。

1.1 二叉树 定义

二叉树是结点的集合。这个集合为空，或者有一个根节点，其余节点分属左右两个二叉子树。
二叉树的结点有如下五种形态：

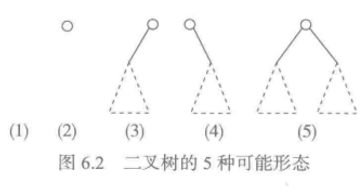
1.2 相关概念

空树：集合为空的二叉树。
单点树：只包含一个根结点的二叉树。
父结点、子节点：相对的概念，根结点是后续关联节点的父结点，后续关联节点是根结点的子节点。二者是一条边直接关联的。
祖先结点、子孙结点：一系列父子结点构成直系的祖先结点和子孙结点。其关联是一系列边形成的从前到后的关联。
树叶结点：没有子结点的结点。
分支结点：有子结点的结点。一个分支结点如果只有一个子节点，必须指明是左节点还是右节点。

度数：一个结点的子节点的个数，显然，二叉树的结点的度数范围为：{0,1,2}。
路径：从祖先结点到子孙结点的一系列关联的边组成一条关联路径。路径的边的条数称为路径的长度。
从某一分支结点到其任意子节点都有唯一路径。
层数：规定根结点的层数为0，某一层的结点到根结点的路径长度即为层数。
高度/深度：所有结点的最大层数。

1.3 二叉树重要性质

1. 非空二叉树的第$i$层至多有$2^i$ 个结点。
2. 高度为$h$的二叉树至多有$2^{h+1}-1$个结点。
3. 对于非空二叉树$T$，如果其页结点的个数$n_0$，度数为2的结点个数为$n_2$，那么有：$n_0=n_2+1$

1.4 特殊二叉树及其性质

1. 满二叉树
   所有分支结点的度数都是2的二叉树。
   性质：满二叉树的叶结点数比分支结点数多1

2. 扩充二叉树
   为二叉树T增加新的叶结点，使原有的结点的度数都为2.则该得到的二叉树为T的扩充二叉树。其中新增的结点称为外部结点，原结点称为内部结点。空树的扩充二叉树规定为空树。

3. 完全二叉树
   对于一个高度为h的二叉树，其0到h-1层的结点度数都是2，最后一层不满的话，所有结点从最左边连续排列。空位都在右边。
   

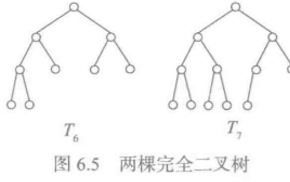
4. 堆
   任一个结点里所存的数据先于或等于其子节点里数据的完全二叉树。如果是小元素优先，则称为小顶堆，反之称为大顶堆。

5. 二叉搜索树（Binary Search Tree）
   二叉搜索树²，或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉搜索树。

   二叉搜索树作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势

   在二叉搜索树中：

   • 若任意结点的左子树不空，则左子树上所有结点的值均不大于它的根结点的值。
   • 若任意结点的右子树不空，则右子树上所有结点的值均不小于它的根结点的值。
   • 任意结点的左、右子树也分别为二叉搜索树

   二叉搜索树是能够高效地进行如下操作的数据结构。

   • 插入一个数值
   • 查询是否包含某个数值
   • 删除某个数值

2. 相关算法

以下面的二叉树为例:

2.1 深度优先遍历

1. 先序遍历：根左右
   ABDHEICFJKG
2. 后序遍历 左右根
   HDEIBJKFGCA
3. 中序遍历 左根右
   DH B EI A JFKCG

2.2 宽度优先遍历

层次遍历法
A BCDEFGHIJK

3. python 类实现

from functools import reduce

class TreeNode:
    def __init__(self,x,left=None,right=None):
        self.val = x
        self.left = left
        self.right = right
        
    def _str(self,type='first'):
        list_node = []
        if self.val:
            str_val = str(self.val)
            str_left = self.left._str(type) if self.left else ""
            str_right = self.right._str(type) if self.right else ""
            if type == 'first':
                list_node = [str_val,str_left,str_right]
            if type == 'middle':
                list_node = [str_left,str_val,str_right]
            if type == 'last':
                list_node = [str_left,str_right,str_val]
        return reduce(lambda a,b:a+b,list_node)
        
    def __str__(self):
        s = ""
        if self.val:
            if self.left:
                s += str(self.left)
            s += str(self.val)
            if self.right:
                s += str(self.right)
        return s


if __name__ == "__main__":
    node_h = TreeNode('H')
    node_i = TreeNode('I') 
    node_j = TreeNode('J')
    node_k = TreeNode('K')

    node_d = TreeNode('D',right=node_h)
    node_f = TreeNode('F',left=node_j,right=node_k)
    node_e = TreeNode('E',right=node_i)
    node_g = TreeNode('G')

    node_b = TreeNode('B',node_d,node_e)
    node_c = TreeNode('C',node_f,node_g)

    node_a = TreeNode('A',node_b,node_c)
    
    print(node_a._str('last'))

4. LeetCode相关题目

• 95:不同的二叉搜索树2
• 104,最大深度

---

参考资料

---

1. 裘宗燕. 数据结构与算法:Python语言描述[M]. 机械工业出版社, 2016 ↩︎

2. 百度百科：二叉搜索树 ↩︎