leading dimension

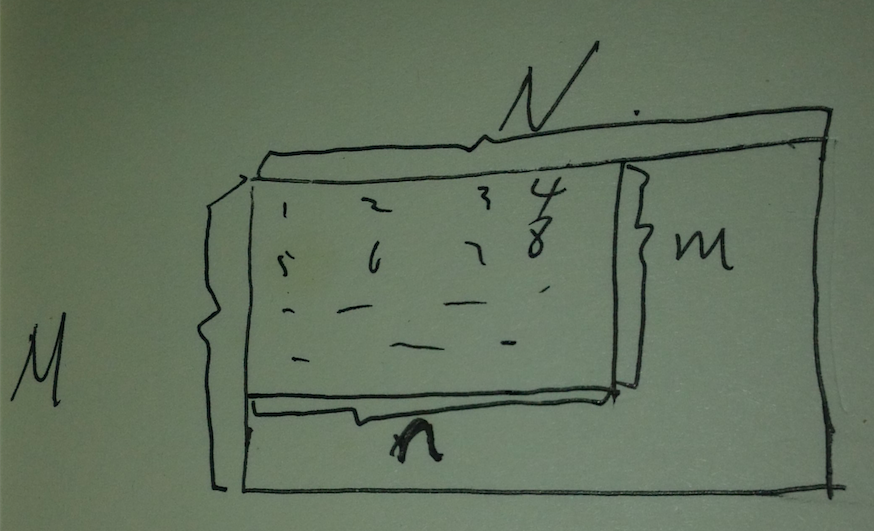
矩阵空间是 3x4，其左上角有一个子矩阵2x3，表示如下

11 22 33 0

44 55 66 0

0   0    0   0

i， j分别表示行索引，列索引

如果用列存储的话，leading dimension = 3(矩阵空间的行个数)， 换算公式是i + j *ld

11 44 0 22 55 0 33 66 0 0 0 0

如果是用行存储， leading dimension = 4(矩阵空间的列个数)，换算公式是 i*ld + j

11 22 33 0 44 55 66 0 0 0 0 0

cublas中矩阵用列存储表示，cusparse中的矩阵用行CNC表示

在cuda中二维数组是按照列存储的，在c中二维数组按照行存储，在c语言中的一个矩阵（二维数组）A = M X K, B = N X K, C = A * Bt = M x N

对于cuda而言（列存储），看到的A矩阵是K x M, B 是 K x N, 计算的C = Bt * A = N x M

计算结果C矩阵在c语言看来就是按照行存储的 M x N

在cuda中，对于A矩阵，不论在cublasSgemm, 是trans还是non-trans，其leading dimension就是 K, 同理对于矩阵B，是转置还是不转置，leading dimension都是K

在cuda中

 设 A' = B = K x N , B' = A = K x M

transa = CUBLAS_OP_T

transb = CUBLAS_OP_N

m = op(A')_row = N

n = op(B')_col = M

k = op(A')_col = op(B')_row = K

lda = A'_row = K

ldb = B'_row = K

ldc = C_row = N

在c语言中有上图的矩阵，矩阵空间是 M x N, 但是只用到了mxn的子矩阵

对cuda而言，它看到的矩阵空间是NxM, 子矩阵是nxm

调用cublasSgemm，m,n,k都是用子矩阵的大小维度，但是lda = N

总结就是，gemm中的n,m,k都是计算的在cuda视角下子矩阵的维度，随着矩阵转置与否变化，但是lda是在cuda视角下矩阵空间的row的大小，并且不随矩阵转置与否变化

参考http://stackoverflow.com/questions/14595750/transpose-matrix-multiplication-in-cublas-howto

The problem is simple: I have two matrices, A and B, that are M by N, where M >> N. I want to first take the transpose of A, and then multiply that by B (A^T * B) to put that into C, which is N by N. I have everything set up for A and B, but how do I call cublasSgemm properly without it returning the wrong answer?

I understand that cuBlas has a cublasOperation_t enum for transposing things beforehand, but somehow I'm not quite using it correctly. My matrices A and B are in row-major order, i.e. [ row1 ][ row2 ][ row3 ]..... in device memory. That means for A to be interpreted as A-transposed, BLAS needs to know my A is in column-major order. My current code looks like below:

float *A, *B, *C;
// initialize A, B, C as device arrays, fill them with values
// initialize m = num_row_A, n = num_row_B, and k = num_col_A;
// set lda = m, ldb = k, ldc = m;
// alpha = 1, beta = 0;
// set up cuBlas handle ...

cublasSgemm(handle, CUBLAS_OP_T, CUBLAS_OP_N, m, n, k, &alpha, A, lda, B, ldb, &beta, C, ldc);

My questions:

Am I setting up m, k, n correctly?

What about lda, ldb, ldc?

Thanks!

Since cuBLAS always assume that the matrices are stored in column-major. You could either transpose your matrices first into colum-major by using cublas_geam(), or

You could treat your matrix A stored in row-major, as a new matrix AT stored in column-major. The matrix AT is actually the transpose of A. For B do the same thing. Then you could calculate matrix C stored in column-major by C=AT * BT^T

float* AT = A;
float* BT = B;

The leading dimension is a param related to the storage, which doesn't change no matter you use the transpose flag CUBLAS_OP_T or not.

lda = num_col_A = num_row_AT = N;
ldb = num_col_B = num_row_BT = N;
ldc = num_row_C = N;

m and n in the cuBLAS GEMM routine are the #rows and #cols of the result matrix C,

m = num_row_C = num_row_AT = num_col_A = N;
n = num_col_C = num_row_BT = num_col_B = N;

k is the common dimension of A^T and B,

k = num_col_AT = num_row_B = M;

Then you could invoke the GEMM routine by

cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_T, m, n, k, &alpha, AT, lda, BT, ldb, &beta, C, ldc);

If you want the matrix C to be stored in row-major, you could calculate the CT stored in column-major with the formula CT = BT * AT^T by

cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_T, n, m, k, &alpha, BT, ldb, AT, lda, &beta, CT, ldc);

Please note you don't have to swap m and n since C is a square matrix in this case.