拉格朗日（Lagrange）插值公式推导及python实现计算

一、引言

1.插值函数的定义：
设函数y=f(x)在区间[a,b]上有定义，且已知在点a≤x0≤x1≤…≤xn≤b上的值y0,y1,…,yn，若存在一简单函数P(x)，使

成立，就称P(x)为f(x)的插值函数，点x0,x1,…,xn称为插值节点，包含插值节点的区间[a,b]为插值区间，求插值函数P(x)的方法称为插值法。
2.插值多项式
若P(x)是次数不超过n的代数多项式，即

其中a0,a1,…an为实数，称P(x)为插值多项式。 有n+1个未知数，我只需要知道n+1个点的函数值就可以解出这n+1个未知数,拉格朗日插值法就是求得这个多项式函数。

二、lagrange插值公式推导

1.用Hn代表所以次数不超过n的多项式集合，于是P(x)∈Hn。将n+1个点带入P(x)可得：

方程的系数矩阵A的行列式是范德蒙德行列式

由于x0,x1,…,xn互不相同，则方程存在唯一的一组解。（插值多项式的存在唯一性）
2.解lagrange多项式,我们先讨论n=1的情形。
假定已知区间[x_k,x_k+1]的端点出函数值yk=f(xk), y_k+1 = f(x_k-1),要求线性多项式满足L1(xk)=yk, L1(x_k+1)=y_k+1 的条件。几何意义如图：

通过这个图我们利用两点式求得如下(这个公式推到属于有手就会嘿嘿，太简单的平面解析几何问题)：


由两点式方程看出，L1(x)是由两个线性函数lk(x)和l_k+1(x)的线性组合得到，其系数分别为yk和y_k+1。线性函数lk(x)和l_k+1(x)又称为线性插值基函数，它们的图形分别如图(a)和(b)所示：

下面讨论n=2的情况，求二次插值多项式L2(x)，使它满足：

可以采用基函数li(x)方法，插值基函数应该满足：

通过这个很容易可以求出插值基函数，例如l_k-1(x)的形式应该为：

其中A为待定系数。
利用插值基函数满足的条件可以得三个插值基函数结果：



它们在区间[xk-1, xk+1]上的图形分别如图（a）,(b),©所示：

(3)现在讨论n+1个节点,用类似上面的方法进行推导。其实不知道大家发现没有它的插值基函数具有很强的规律性。n+1个插值基函数如下：

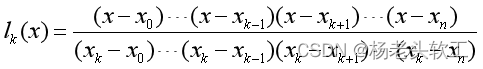
进而可以得到n次插值多项式，也称为Lagrange插值多项式。

三、代码实现计算

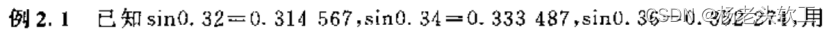
抛物线插值0.3367.
代码：

import numpy as np
x1=0.32
y1=np.round(np.sin(0.32),6)
y1
x2=0.34
y2=np.round(np.sin(0.34),6)
y2
x3=0.36
y3=np.round(np.sin(0.36),6)
y3
#原函数f=sin(x)
def f(x):
return np.sin(x)

x=np.linspace(0,np.pi,1000)
y=f(x)
#原图
import matplotlib.pyplot as plt
plt.figure(figsize=(10,8),dpi=100)
plt.plot(x,y)
plt.plot(x1,y1,'r*')
plt.plot(x2,y2,'r*')
plt.plot(x3,y3,'r*')
plt.show()

#Lagrange插值函数
def lagrange_f(x,x1,x2,x3,y1,y2,y3):
    l1=y1*(x-x2)*(x-x3)/((x1-x2)*(x1-x3))
    l2=y2*(x-x1)*(x-x3)/((x2-x1)*(x2-x3))
    l3=y3*(x-x1)*(x-x2)/((x3-x1)*(x3-x2))
    return l1+l2+l3
x_=0.3367
result=np.round(lagrange_f(0.3367,x1,x2,x3,y1,y2,y3),6)
result
new_y=lagrange_f(x,x1,x2,x3,y1,y2,y3)
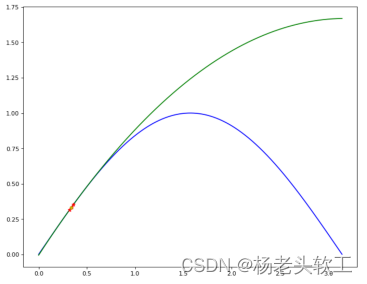
#原图和拟合图
plt.figure(figsize=(10,8),dpi=80)
plt.plot(x,y,'b')
plt.plot(x,new_y,'g')
plt.plot(x1,y1,'r*')
plt.plot(x2,y2,'r*')
plt.plot(x3,y3,'r*')
plt.plot(x_,result,'y*')
plt.show()