使用朴素贝叶斯对iris数据集进行分类

贝叶斯分类是数学性较强的分类方法，在处理多属性问题的分类时，主要用到下面两个公式：

 

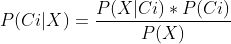
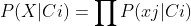
第二个公式之所以成立，是因为在贝叶斯分类中进行了各属性均与分类标签独立的假设。即X与Ci独立，则有：

，，

 

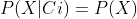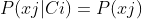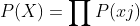
import random
import numpy as np
from math import e
from math import pow
from sklearn.datasets import load_iris

iris=load_iris()
n_tot,n_attr=iris.data.shape
n_train=120;n_test=30;n_target=3;mm=5

book=np.zeros(150,dtype=int)

for i in range(n_test):#每五个样本中，选一个作为测试样本
    val=5*i+random.randint(0,4)
    book[val]=1

data_train=np.zeros((n_tot,5))
data_test=np.zeros((n_tot,5))
cnt1=0;cnt2=0

for i in range(n_tot):#data_train为训练样本，data_test为测试样本
    if book[i]==0:
        for j in range(n_attr):
            data_train[cnt1][j]=iris.data[i][j]
        data_train[cnt1][n_attr]=iris.target[i]
        cnt1+=1
    else:
        for j in range(n_attr):
            data_test[cnt2][j]=iris.data[i][j]
        data_test[cnt2][n_attr]=iris.target[i]
        cnt2+=1

cnt=np.zeros((5,5))
average=np.zeros((5,5))
deviation=np.zeros((5,5))
pro_attr=np.zeros(5)

for i in range(n_target):#average[i][j]代表所有标签为i的样本中，第j个属性的均值
    for j in range(n_attr):
        for k in range(n_train):
            if data_train[k][n_attr]==i:
                average[i][j]+=data_train[k][j]
                cnt[i][j]+=1.0

for i in range(n_target):
    for j in range(n_attr):
        average[i][j]/=cnt[i][j]

for i in range(n_target):#deviation[i][j]代表所有标签为i的样本中，第j个属性的方差
    for j in range(n_attr):
        for k in range(n_train):
            if data_train[k][n_attr]==i:
                deviation[i][j]+=(data_train[k][j]-average[i][j])*(data_train[k][j]-average[i][j])

for i in range(n_target):
    for j in range(n_attr):
        deviation[i][j]/=cnt[i][j]

for i in range(n_train):#pro_attr[i]代表标签为i的样本占所有样本的比例
    val=int(data_train[i][n_attr])
    pro_attr[val]+=1.0

for i in range(n_target):
    pro_attr[i]/=n_train



cnt_correct=0
for i in range(n_test):
    maxx=0.0;ans=0.0
    for j in range(n_target):#求P(Cj|X)
        tmp=pro_attr[j]
        for k in range(n_attr):#求P(Xk|Cj)
            val=pow(e,-((data_test[i][k]-average[j][k])*(data_test[i][k]-average[j][k]))/(2.0*deviation[j][k]*deviation[j][k]))
            tmp*=val;
        if maxx<tmp:
            maxx=tmp
            ans=j
    if ans==data_test[i][n_attr]:
        cnt_correct+=1

print(cnt_correct,n_test)