线性回归:
线性回归假设特征和结果满足线性关系,每个特征都有一个参数,也就是它的影响力。而且每个特征变量可以首先映射到一个函数,然后再参与线性计算。这样就可以表达非线性关系。
只有一个自变量的情况叫做简单回归, 多个自变量情况的叫做多元回归
简单回归:y= a + b*x
多元回归:h(x)= θ0 + θ1*x1 + θ2*x2 + ...
损失函数:j(θ), 对x(i)的估计值与真实值y(i)差的平方和
我们的目标是最小化j(θ)。可以通过最小二乘法,或者梯度下降法来确定这个
最小二乘法:直接计算
梯度下降法:首先对θ赋一个初值,改变θ的值,使得J(θ)按梯度下降的方向进行减少。
梯度方向由J(θ)对θ的偏导数确定,由于求的是极小值,因此梯度方向是偏导数的反方向
迭代更新的方式,批梯度下降:对全部的训练数据求得误差后再对θ进行更新,这种方法能够不断收敛;
增量梯度下降:每扫描一步都要对θ进行更新,这种方法结果可能不断在收敛处徘徊。
一般来说,梯度下降法收敛速度还是比较慢的。
逻辑回归:(处理分类)
分类是预测离散或标称值,而回归用于预测连续或有序值。
回归是连续型模型,而且受噪声影响比较大,一般不用做分类。如果非要做分类,可以使用逻辑回归处理二分类问题。
逻辑回归本质上是线性回归,只是在特征到结果的映射再做一个映射,将连续值映射到0和1上。即先对特征线性求和,然后使用函数g(z)作为假设函数来预测。
 线性与逻辑回归解析
线性与逻辑回归解析





 本文探讨了线性回归的基本原理及其应用场景,包括简单回归与多元回归,并介绍了如何通过最小二乘法和梯度下降法来优化模型。此外,还讨论了逻辑回归作为一种分类方法的应用,特别是针对二分类问题。
本文探讨了线性回归的基本原理及其应用场景,包括简单回归与多元回归,并介绍了如何通过最小二乘法和梯度下降法来优化模型。此外,还讨论了逻辑回归作为一种分类方法的应用,特别是针对二分类问题。
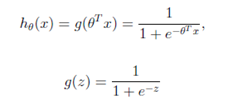
















 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








