复数运算与解析几何-CSDN博客

选项A

Z1和Z2是两个不同的复数， $Z = (1-t)Z1 + tZ2$ ，其中 t 是一个实数，且t大于0小于1，Arg(w)是非零复数w的主幅角，我们知道Arg是指位矢（shǐ）的幅角，位矢可以在复平面以及实轴上确定一个复数，我画一下：

纵轴是 $Im$ ，横轴是 $Re$ 。

假设绿色就是我们的复数，也就是Z，

那么 $Arg(Z)$ 就代表这个角，所以 $\varphi = Arg(Z)$ ，所以 $\varphi = Arg(Z)$ ，这就是题干第二部分给我们的信息。

现在依次看一下这些选项（如图）并进行判断：

要知道的一点是，这是一道多选题，那么来判断一下。我们先来A选项：

$A) |z - z_{1}| + |z - z_2| = |z_1 - z_2|$

首先找出 $|z-z_1|$ 的幅值，我写一下，先看 $z$ ， $z$ 就是这个式子 $z = (1-t)z_1 + tz_2$ ：

$|z-z_1|=|z_1-tz_1+tz_2-z_1|$

消掉 $z_1$ ，这里可以把t作为因子提出来，就等于：

$|z-z_1|=|z_1-tz_1+tz_2-z_1|=|t(z_2-z_1)|$

这就是 $|z-z_1|$ 也就是这里的第一项。

接下来计算一下 $|z-z_2|$ ：

$|z-z_2| =|(1-t)z_1 + tz_2-z_2|$

这项可以提出一个 $(t-1)$ ，把 $z_2$ 作为公因子提出来，所以这部分等于 $|(1-t)z_1|$ 。

$|z-z_2| =|(1-t)z_1 + tz_2-z_2|=|(1-t)z_1+(t-1)z_2|$

现在看一下这两个相加会如何，也就是选项A，把这两个加起来，看看能否化简，结果是：

$|t(z_2-z_1)|+...$

继续化简 $|(1-t)z_1+(t-1)z_2|$ ，等于

$|(1-t)z_1-(1-t)z_2|$

我只是替换一下 $-(1-t)$ 就等于 $t-1$ ，再乘以 $z_2$ ，而在这边也有 $1-t$ ，所以就成了，把 $1-t$ 提出来：

$|(1-t)(z_1-z_2)|$

最后我们得出：

$|t(z_2-z_1)|+|(1-t)(z_1-z_2)|$

这是A选项简化之后的效果，现在看看能不能再进一步简化。t是一个系数，位于0和1之间，这是题干告诉我们的，t位于0和1之间，这是个正数， $(1-t)$ 这也是正数，t比0大，比1小，所以这也是个正数，这只是个系数，所以其实它就等于，t仅仅是决定幅值大小的系数，所以这个式子就等于：

$|t||z_2-z_1|+|1-t||z_1-z_2|$

t仅仅是个系数，弄清楚一点， $|z_1-z_2|=|z_2-z_1|$ ，这两个向量是指向不同方向的，所以这个复数和这一个互为相反数，但它们的绝对值或者说是幅值是一样的。把 $|z_2-z_1|$ 写下来，这样做是为了得到同样的项，可以把 $|z_2-z_1|$ 提取出来：

$|t||z_2-z_1|+|1-t||z_2-z_1|$

它和 $|z_1-z_2|$ 是一样的，因为它们的区别仅仅是方向不同，现在该怎么做呢？t的绝对值，记住t是正的，所以 $|t|=t$ ， $|1-t|$ 也是正的，所以就是 $1-t$ ，所以可以把它提取出来，也就得到了：

$(t+1-t)|z_2-z_1|$

t消去了，前面剩下了一个1，所以最终结果就是：

$(t+1-t)|z_2-z_1| =|z_2-z_1|$

所以选项A是对的。二者相加确实等于 $|z_2-z_1|$ 。

选项B

z-z1的幅角等于z-z2的幅角：

$B) Arg(z-z_1) = Arg(z-z_2)$

之前我们已经化简得到 $z-z_1$ 等于 $|t(z_2-z_1)|$ ，所以：

$Arg(|t(z_2-z_1)|)$

我们调用前面算出的结果，由于这部分等价于绝对值符号内部的部分，也就是这儿这部分，因而：

$Arg(t\cdot (z_2-z_1)) =Arg(z-z_2)$

那么，问题是 $z-z_2$ 是等于多少呢？这里已经计算出结果，就是这部分。

$Arg(t\cdot (z_2-z_1)) =Arg((1-t)(z_1-z_2))$

这里我们得到统一的形式，把这乘上-1，然后把这个也乘上-1，连续乘以两个-1不改变式子。所以这就等于，或者说表达式就等于：

$Arg(t\cdot (z_2-z_1)) =Arg((1-t)(z_1-z_2))$

$=Arg((t-1)(z_2-z_1))$

记住我刚才所做的，我们来思考一下，这里 $(1-t)$ 我乘以一个-1，这个 $(z_1-z_2)$ 也乘以-1，两部分都乘以-1，也就相当于乘了两次-1，其实相当于乘以1。因此两个相乘项里面互换位置。

这个等式成立吗？ $Arg(t\cdot (z_2-z_1))$ 是不是真的等于 $Arg((t-1)(z_2-z_1))$ ，我们来思考一下，我画一个坐标图：

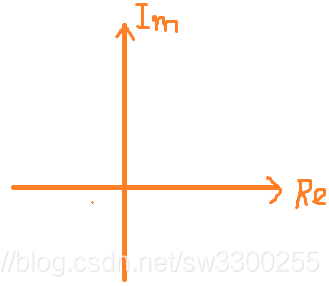
然后在坐标图上表示向量 $(z_2-z_1)$ ，这部分就是向量 $(z_2-z_1)$ ：

现在， $t\cdot (z_2-z_1)$ 等于什么？关于 t ，我们知道它介于0和1之间，因此乘上 t 相当于缩短了向量 $z_2-z_1$ 的长度，不用管是多长，假设就是这部分，它就表示向量 $t\cdot (z_2-z_1)$ ：

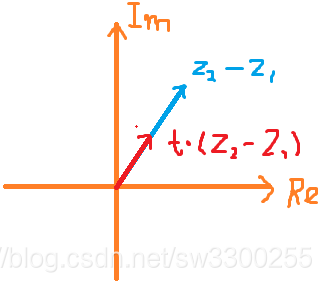
现在， $(t-1)(z_2-z_1)$ 等于什么？t -1 要记得 t 介于0和1之间，所以 t 要小于 1，因此 t - 1，也就是这部分 $(t-1)$ 应该是一个负数。因此我们要用负数来对向量 $z_2-z_1$ 进行比例缩放，那么这部分， $(t-1)(z_2-z_1)$ 将会变成这样：

绿色线就是 $(t-1)(z_2-z_1)$ ，而幅角就是这些向量和实轴的夹角，所以这部分 $Arg(t\cdot (z_2-z_1))$ ，这个幅角就是这个角度：

我们可以把它设为 $\phi$ ：

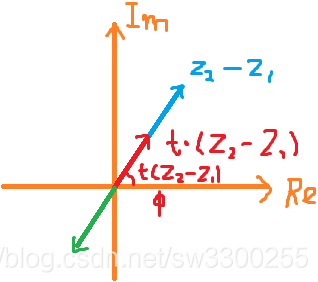
那么这部分的幅角是多少？它就必须加上π或者加上180度，就是要绕半圆周：

因此它们不是同一个角，无论这里数字是多少，这个数都要加上π，当然也可以减去π：

但是它们肯定不会是相等的。因此我们可以排除了选项B。看完B后，我们直接看D，因为它和选项B很相似。

选项D

$D) Arg(z-z_1) = Arg(z_2-z_1)$

选项D告诉我们，现在我们还不知道要验证才知道 $z-z_1$ 的幅角是否等于 $z_2-z_1$ 的幅角。所以我们来思考一下，当然，我们已经计算过 $z-z_1$ 等于什么，它就等于这部分 $t(z_2-z_1)$ ，所以这种表述就等价于 $Arg(z-z_1)$ ：

$Arg(z-z_1)=t(z_2-z_1)$

直接使用上一集的计算结果 $t(z_2-z_1)$ 。是否等于Arg(z_2-z_1)？让我们再来画一次坐标图，事实上，我们可以在这个坐标图里面画出 $z_2-z_1$ 这部分。我们已经得到了它的幅角就等于这个角度：

紫色就是 $z_2-z_1$ 的幅角，也就是选项D中的 $t(z_2-z_1) =Arg(z_2-z_1)$ 的 $z_2-z_1$ 的幅角，而 $t(z_2-z_1)$ 就是把这个向量缩放后，用橙色表示的部分，很明显 t 是一个正数，所以这个向量方向不变，仅仅是长度上的缩放这个向量和这个向量，或者说这个复数和这个复数，他们的方向是相同的，也就是它们和实轴的夹角相等，红色表示的向量或者说复数表示的是这部分 $t(z_2-z_1)$ ，而蓝色的线就是表示 $z_2-z_1$ ，显然他们的方向是相同的，幅角是相同的，所以选项D是正确项。

选项C

C选项给出了一个行列式，并说它等于0。我们来看他们是否成立，我们就可以把它们乘出来，看看有没有什么意思的地方，而且我们还可以借助前面的结果，A选项我们验证过了，算A选项时，我们求出了，我们得到了等式：

$z-z_1=t(z_2-z_1)$

所以行列式的这一项 $z-z_1$ ，它就等于 $t(z_2-z_1)$ 。

这里有趣的是下面也有一个 $z_2-z_1$ ，我们就逐渐发现里相似的地方了，然后这一项 $\overline{z}-\overline{z_1}$ 如果对这相减的两个数都求共轭，对两个数都求共轭， $z$ 的共轭减去 $z_1$ 的共轭就等于：

$\overline{z}-\overline{z_1} = t(\overline{z_2}-\overline{z_1})$

而我们知道求共轭时，我实际上是对复数虚部的符号取反，而对这整个运算都求共轭就相当于把全部复数的虚部符号取反，结果就是虚部都变成了原来的相反数，我们就是这样做的，这就表示把虚部都取反了，如果你想确切地求共轭就可以令它等于A+Bi而第二项等于A1+B1i就可以进行运算了，但我想这都是很直观的，也就是只需要把这些复数的，全部虚部符号取反就行了。

有了这两个等式： $z-z_1=t(z_2-z_1)$ 、 $\overline{z}-\overline{z_1} = t(\overline{z_2}-\overline{z_1})$ 。求这个行列式就相当容易了， $z_2-z_1$ 它就变成 $t(z_2-z_1)$ ，而这项 $\overline{z_2}-\overline{z_1}$ 变成 $t(\overline{z_2}-\overline{z_1})$ ，然后是 $z_2-z_1$ ，而最后这一项是 $\overline{z_2}-\overline{z_1}$ ，C选项就表示这两个对角相乘，也就是：