小学二年级数学题蕴含的算法 -- 全排列算法

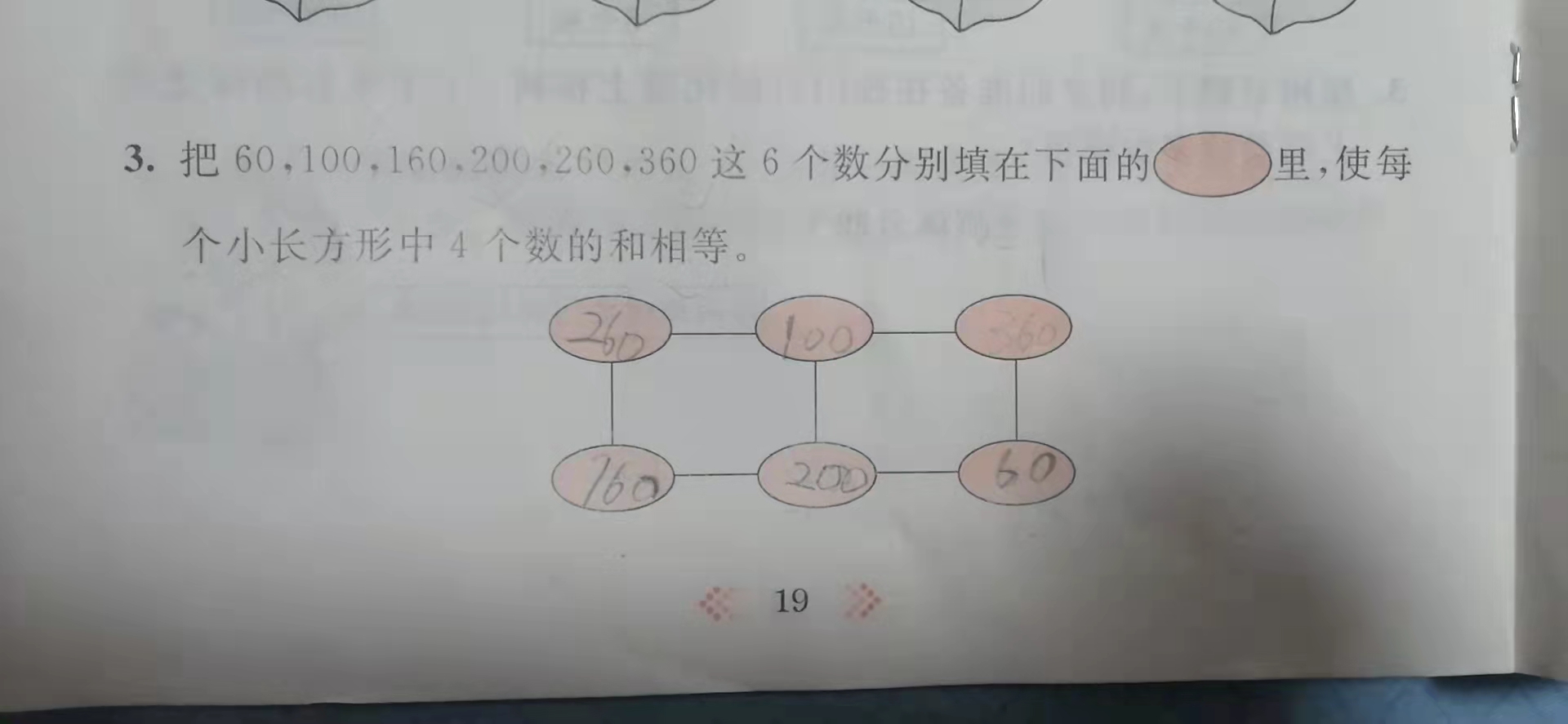
上面数学题是同学家孩子小学二年级的题目，把 60， 100， 160， 200， 260， 360 共6个数字填入如图的椭圆形里面，使得左边的矩形之和等于右边矩形之和。

如果用数学的方法去解，就是左边一列之和等于右边一列之和，中间一列是公共的，是什么无所谓。尝试几次很快就能找到一个答案了。

如果用程序员的思维去解决呢？如何找到所有可能的答案呢？我们先给椭圆形编号，按从上到下，从左到右的顺序，依次为 0， 1， 2 ，3 ，4 ，5， 如下所示：

0 3 4

1 2 5

定义一个数组 int nums[5], 问题转化为： 什么时候 a[0]+a[1]+a[2]+a[3] = a[2]+a[3]+a[4]+a[5] ?

a[0] -- a[5]的值从60， 100， 160， 200， 260， 360中选择一个，不能重复。

显然，只需要获取这些数字的全排列，然后满足a[0]+a[1]+a[2]+a[3] = a[2]+a[3]+a[4]+a[5] 的就是一个答案。此题的关键在于全排列算法，STL提供了next_permutation和prev_permutation两个函数可以很简单的解决问题？但是如果自己来写算法呢？下面我写了一个很简单的算法，基本思想就是递推，如下：

1个数：1

2个数：12， 21

3个数：

在12的0,1,2位置插入数字3得：312，132,123

在21的0,1,2位置插入数字3得：321,231,213

4个数：

在312的0,1,2,3位置插入数字4：4312,3412,3142,3124

在132的0,1,2,3位置插入数字4：4132,1432,1342,1324

在123的0,1,2,3位置插入数字4：4123,1423,1243,1234

在321的0,1,2,3位置插入数字4：4321,3421,3241,3214

在231的0,1,2,3位置插入数字4：4231,2431,2341,2314

在213的0,1,2,3位置插入数字4：4213,2413,2143,2134

以此类推，算法如下：

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    int nums[] = {60, 100, 160, 200, 260, 360};
    vector< vector<int> > ls1 = { {60} }, ls2;
    vector< vector<int> > *plsNow  = &ls1, *plsNext = &ls2, *plsTmp;
    vector<int> vOld, vNew;

    for (int i = 1; i < 6; i++) {
        plsNext->clear();
        for (int j = 0; j < plsNow->size(); j++) {
            vOld = plsNow->at(j);
            for (int k = 0; k <= vOld.size(); k++) {
                vNew = vOld;
                vNew.insert(vNew.begin() + k, nums[i]);
                plsNext->push_back(vNew);
            }
        }
        plsTmp  = plsNow;
        plsNow  = plsNext;
        plsNext = plsTmp;
    }

    int total = 0;
    for (int i = 0; i < plsNow->size(); i++) {
        vNew = plsNow->at(i);
        if (vNew[0] + vNew[1] + vNew[2] + vNew[3] != vNew[2] + vNew[3] + vNew[4] + vNew[5]) {
            continue;
        }
        std::cout << vNew[0] << "\t" << vNew[2] << "\t" << vNew[4] << endl;
        std::cout << vNew[1] << "\t" << vNew[3] << "\t" << vNew[5] << endl;
        std::cout << endl;
        total++;
    }
    std::cout << "all: " << plsNow->size() << ",  match: " << total << endl;
}

运行结果：

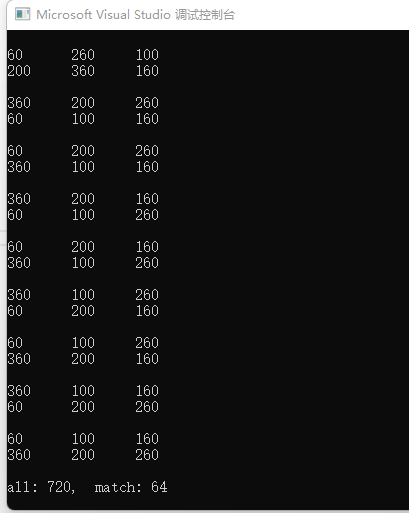
一共720种排列，其中64种排列满足题目要求，即找到了64个答案！

小学数学也不容易吧 :)