【强化学习】时序差分方法

sword_csdn

已于 2022-08-11 11:53:12 修改

阅读量1k

点赞数

分类专栏：机器学习文章标签：算法

于 2021-06-25 19:20:27 首次发布

本文链接：https://blog.csdn.net/sword_csdn/article/details/118144693

版权

机器学习专栏收录该内容

40 篇文章 8 订阅

订阅专栏

时序差分预测

DP、MC、TD之间的区别

随机游走问题比较批量训练下的TD(0)和常量MC的性能

Sarsa：On-policy 时序差分（TD）控制

Q-learning：Off-policy TD方法

on-policy和off-policy的区别

Maximization Bias和Double Learning

Expected Sarsa

Double Learning

时序差分预测

时序差分方法结合了蒙特卡洛方法和动态规划的思想，在强化学习中应用最为广泛。

（1）直接从智能体与环境交互的经验中学习。

（2）无须等待交互的结果，可以边交互边学习，不需要等整个episode结束。

预测问题：即给定强化学习的5个要素：状态集 $S$ ，动作集 $A$ ，即时奖励 $R$ ，衰减因子 $\gamma$ ，给定策略 $\pi$ ，求解该策略的状态价值函数 $v(\pi )$ 。

控制问题：也就是求解最优的价值函数的策略。给定强化学习的5个要素：状态集 $S$ ，动作集 $A$ ，即时奖励 $R$ ，衰减因子 $\gamma$ ，探索率 $\epsilon$ ，求解最优的动作价值函数 $q_{*}$ 和 $\pi _{*}$ 。

已知every - visit的MC算法的价值计算函数是

在MC方法中，必须要等到episode结束，有了return之后才能更新，在有些应用中episode时间很长，或者是连续型任务，根本没有episodes。而TD方法只需要等到下一个time step即可，即在时刻 $T+1$ 时，TD方法立即形成一个target，并使用观测到的Reward（ $R_{t+1}$ ）和估计的 $V_{t+1}$ 进行更新。比如最简单的TD(0)算法：

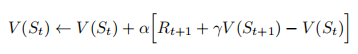
在TD(0)中，括号里的数值是一种误差，它衡量的是 $S_{t}$ 的估计值与更好的估计 $R_{t+1}+\gamma V(S_{t+1})$ 之间的差异，这个数值被称为TD误差。

$\delta_{t}=R_{t+1}+\gamma V(S_{t+1})-V(S_{t})$

DP、MC、TD之间的区别

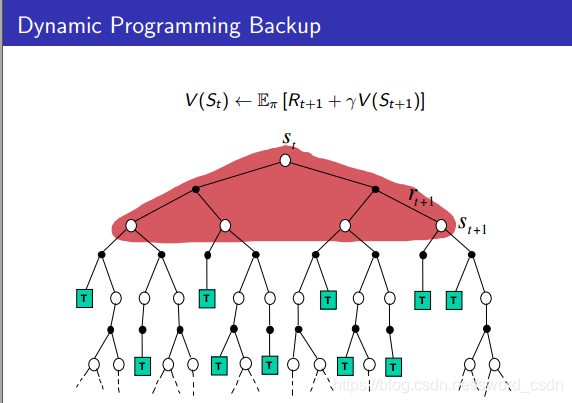
由上图可以看出，DP算法在计算某个状态 $S_{t}$ 的价值时，会考虑接下来所有可能的状态 $S_{t+1}$ 以及切换状态后所得 $r_{t+1}$ 。

MC在更新一个状态时，只考虑其中一个分支（episode）来更新。所以MC需要生成很多个分支来提高准确性。

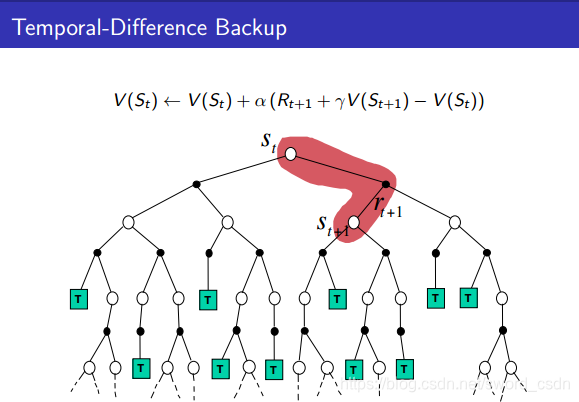
TD算法只需要考虑切换状态后所得奖励 $r_{t+1}$ 和 $S_{t+1}$ 。

随机游走问题比较批量训练下的TD(0)和常量 $\alpha$ MC的性能

如上图所示，批量TD方法在均方根误差上比MC表现得更好。

Sarsa：On-policy 时序差分（TD）控制

这里学习的是行为价值函数 $q_{\pi}$ ，对于on-policy方法，我们必须顾及在策略 $\pi$ 下所有状态 $s$ 以及行为 $a$ 所对应的 $q_{\pi}(s,a)$ ，所采用的估计方法和评估 $v_{\pi}$ 差不多。只是前面是根据状态到状态转换来估计的状态价值，而在此处是根据状态-行为到状态-行为的转换来估计状态-行为的价值

Windy Gridworld Playground环境介绍

如下图所示，我们从S出发，要到达G，有上、下、左、右四个方向可以走，下面各自0,1,2表示风力，也就是我们在不同的列会受到风力的影响，导致实际的方向和我们走的会有区别，每移动一步只要不是进入目标位置都给予一个-1的惩罚，直到进入目标位置后获得奖励0同时永久停留在该位置。现在要求解的问题是应遵循怎样的策略才能尽快从起始位置到达目标位置。

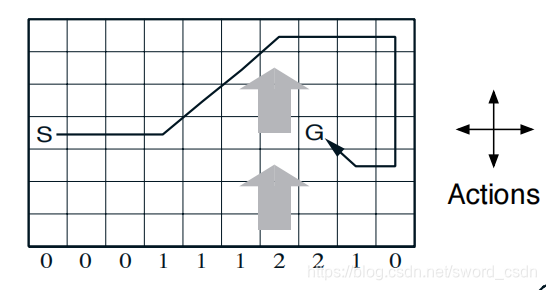
代码实现

import numpy as np
import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as plt

# 世界的高度
WORLD_HEIGHT = 7

# 世界的宽度
WORLD_WIDTH = 10

# 横轴，每一列的风阻的力量
WIND = [0, 0, 0, 1, 1, 1, 2, 2, 1, 0]

# 可能的行为
ACTION_UP = 0
ACTION_DOWN = 1
ACTION_LEFT = 2
ACTION_RIGHT = 3

# 探索的概率
EPSILON = 0.1

# Sarsa 步长
ALPHA = 0.5

# 到达目标前，每一步的收益
REWARD = -1.0
# 起点
START = [3, 0]
# 终点
GOAL = [3, 7]
# 行为列表
ACTIONS = [ACTION_UP, ACTION_DOWN, ACTION_LEFT, ACTION_RIGHT]

def step(state, action):
    i, j = state
    # 每一列的风阻只会影响水平方向的移动
    if action == ACTION_UP:
        return [max(i - 1 - WIND[j], 0), j]
    elif action == ACTION_DOWN:
        return [max(min(i + 1 - WIND[j], WORLD_HEIGHT - 1), 0), j]
    elif action == ACTION_LEFT:
        return [max(i - WIND[j], 0), max(j - 1, 0)]
    elif action == ACTION_RIGHT:
        return [max(i - WIND[j], 0), min(j + 1, WORLD_WIDTH - 1)]
    else:
        assert False

#每一幕的操作，每一局
def episode(q_value):
    # track the total time steps in this episode
    time = 0
    # 初始化状态
    state = START
    # 基于epsilon-greedy算法选择一个行为
    if np.random.binomial(1, EPSILON) == 1:
        #R = np.random.binomial(n,p,size)
        #n：一次实验的样本数
        #p：试验成功的概率
        #size：试验的次数
        #R：一个/列数字
        action = np.random.choice(ACTIONS)
    else:
        values_ = q_value[state[0], state[1], :]
        action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])

    # keep going until get to the goal state
    while state != GOAL:
        next_state = step(state, action)
        if np.random.binomial(1, EPSILON) == 1:
            next_action = np.random.choice(ACTIONS)
        else:
            values_ = q_value[next_state[0], next_state[1], :]
            next_action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])

        # Sarsa update
        q_value[state[0], state[1], action] += \
            ALPHA * (REWARD + q_value[next_state[0], next_state[1], next_action] -
                     q_value[state[0], state[1], action])
        state = next_state
        action = next_action
        time += 1
    return time

def sarsa():
    q_value = np.zeros((WORLD_HEIGHT, WORLD_WIDTH, 4))
    episode_limit = 500

    steps = []
    ep = 0
    while ep < episode_limit:
        steps.append(episode(q_value))
        # time = episode(q_value)
        # episodes.extend([ep] * time)
        ep += 1

    steps = np.add.accumulate(steps)

    plt.plot(steps, np.arange(1, len(steps) + 1))
    plt.xlabel('Time steps')
    plt.ylabel('Episodes')

    plt.savefig('./sarsa.png')
    plt.close()

    # display the optimal policy
    optimal_policy = []
    for i in range(0, WORLD_HEIGHT):
        optimal_policy.append([])
        for j in range(0, WORLD_WIDTH):
            if [i, j] == GOAL:
                optimal_policy[-1].append('G')
                continue
            bestAction = np.argmax(q_value[i, j, :])
            if bestAction == ACTION_UP:
                optimal_policy[-1].append('U')
            elif bestAction == ACTION_DOWN:
                optimal_policy[-1].append('D')
            elif bestAction == ACTION_LEFT:
                optimal_policy[-1].append('L')
            elif bestAction == ACTION_RIGHT:
                optimal_policy[-1].append('R')
    print('Optimal policy is:')
    for row in optimal_policy:
        print(row)
    print('Wind strength for each column:\n{}'.format([str(w) for w in WIND]))

if __name__ == '__main__':
    sarsa()

Q-learning：Off-policy TD方法

Q-learning算法的更新公式定义如下：

在这个公式我们可以看出被学习的行为价值函数Q直接的更新方向是最佳行为价值函数 $q_{*}$ ，与Agent所遵循的行为策略无关。

在“在悬崖边上行走”的例子中，Sarsa算法和Q-Learning的表现迥异，如下图所示：

训练一段时间后，Q-Learning学到了最优策略，即沿着悬崖边上走的策略，但是由于动作是通过 $\epsilon$ -贪心的方式来选择的，所以智能体偶尔会“掉入悬崖” ，与之相比，Sarsa则考虑了动作被选取的方式，学到了一条通过网格上半部分的路径，路径虽然长，但是很安全。

on-policy和off-policy的区别

on-policy：生成样本的policy（value function）跟网络更新参数时使用的policy（value function）相同。典型为SARSA算法，基于当前的policy直接执行一次动作选择，然后用这个样本更新当前的policy，因此生成样本的policy和学习时的policy相同，算法为on-policy算法。该方法会遭遇探索-利用的矛盾，光利用目前已知的最优选择，可能学不到最优解，收敛到局部最优，而加入探索又降低了学习效率。epsilon-greedy 算法是这种矛盾下的折衷。优点是直接了当，速度快，劣势是不一定找到最优策略。

off-policy：生成样本的policy（value function）跟网络更新参数时使用的policy（value function）不同。典型为Q-learning算法，计算下一状态的预期收益时使用了max操作，直接选择最优动作，而当前policy并不一定能选择到最优动作，因此这里生成样本的policy和学习时的policy不同，为off-policy算法。先产生某概率分布下的大量行为数据（behavior policy），意在探索。从这些偏离（off）最优策略的数据中寻求target policy。当然这么做是需要满足数学条件的：假設π是目标策略, µ是行为策略，那么从µ学到π的条件是：π(a|s) > 0 必然有 µ(a|s) > 0成立。两种学习策略的关系是：on-policy是off-policy 的特殊情形，其target policy 和behavior policy是一个。劣势是曲折，收敛慢，但优势是更为强大和通用。其强大是因为它确保了数据全面性，所有行为都能覆盖。

Maximization Bias和Double Learning

如Q-learning更新Q表的公式：

即，每个状态动作价值 $Q(S,A)$ ，选择用下一步最大的状态动作价值 $max_{a}Q(S_{t+1},a)$ 来更新。由此可见Q-learning会倾向于将当前局面下一时刻的最优动作价值作为当前局面评估值的更新方向。但是当这个最优状态动作价值是noise又抑或是reward满足某个分布的随机值时，会产生最大化偏差（Maximization Bias）。

举例子进一步说明

如下图所示：

有两个非终止状态A和B，终止状态（灰色矩形）表示终止态T，起始状态是A，选择向右的action会转移到终止态并或者0奖赏值，选择向左的action会转移状态B并获得0奖赏值，对于状态B可以有1个或多个动作，所有动作都会以概率为1转移到终止态，每个动作的奖赏值服从 $N(-0.1,1)$ 的高斯分布。

如果用Q-learning求解

假设状态B后有10个动作，则当Q-learning从状态A开始采样，并用于更新 $Q(A,left)$ ，此时，会先分别计算状态B下的所有action对应的Q值，然后选择最大的Q值和奖赏作为A-left的更新，如下所示

$Q(A,left)\leftarrow Q(A,left)+\alpha[0+\gamma max[Q(B,a_{1}),...,Q(B,a_{10})]-Q(A,left)]$

而由于B的所有动作奖赏服从 $\mu=-0.1<1$ 的分布，所以真实值应该是

$Q(A,left)=\gamma E[Q(B,a)]=\gamma*\mu=-0.1\gamma<0=Q(A,right)$

由于噪声的存在，使得少量 $Q(B,a_{i})>0$ ，因此有可能

$Q(A,left)=\gamma max[Q(B,a_{1}),...,Q(B,a_{10})]>0=Q(A,right)$

这导致在计算状态A的最优动作时，起初会出现很多 $A^{*}=left$ ，直到状态B下大部分的动作都是 $Q(B,a_{i})<0$ 时， $Q(A,left)$ 才逐渐降低到0以下，实验结果如图所示（其中 $\alpha=0.1,\epsilon=0.1,\gamma=0.9$ ）

Expected Sarsa

Q-learning公式中的max操作导致了Maximization Bias，因此想要消除Bias，则让更新操作与max操作解耦，并且要让最接近真实价值的 $Q(B,a)$ 来更新 $Q(A,left)$ 。这个“近似”可以有以下两种方法：

（1）用期望 $Q$ 值作为 $S$ 的更新。

（2）从 $S_{t+1}$ 的Q值分布中随机选取action $a$ ，将其 $Q(S_{t+1},a)$ 作为当前 $S$ 的更新。

（1）的思想就是Expected Sarsa，它把max操作换成了求期望，最后更新公式就变成了

$Q(S_{t},A_{t})\leftarrow Q(S_{t},A_{t})+\alpha[R_{t+1}+\gamma \sum_{a}\pi(a|S_{t+1})Q(S_{t+1},a)-Q(S_t,A_t)]$

Double Learning

Double Learning算法讲样本划分为两个集合，并用它们学习两个独立的估计 $Q_{1}(a)$ ， $Q_{2}(a)$ ，来近似 $q(a)$ 。首先使用其中一个估计，比如 $Q_{1}(a)$ ，来确定具有最大价值的动作 $A^*=argmax_{a}Q_{1}(a)$ ，再用另一个 $Q_{2}$ 来计算其价值的估计 $Q_{2}(A^{*})=Q_{2}(argmax_{a}Q_{1}(a))$ ，由于 $E[Q_2(A^*)|=]=q(A^*)$ ，所以这个估计是无偏的。交换两个估计再执行一遍上面的过程，那么就可以得到另一个无偏的估计 $Q_1(argmax_aQ_2(a)$ 。这就是DL的思想。

sword_csdn

关注

0
点赞
踩
10

收藏

觉得还不错? 一键收藏
1
评论
【强化学习】时序差分方法

时序差分方法结合了蒙特卡洛方法和动态规划的思想，在强化学习中应用最为广泛。（1）直接从智能体与环境交互的经验中学习。（2）无须等待交互的结果，可以边交互边学习，不需要等整个episode结束。预测问题：即给定强化学习的5个要素：状态集，动作集，即时奖励，衰减因子，给定策略，求解该策略的状态价值函数。控制问题：也就是求解最优的价值函数的策略。给定强化学习的5个要素：状态集，动作集，即时奖励，衰减因子，探索率，求解最优的动作价值函数和。已知every - visit的MC算法的价值计算函数是
复制链接

扫一扫