简单线性回归问题——线性模型【蒙哥马利】第二章部分课后习题代码

利用R语言求解线性模型中的简单线性回归问题，涉及：
关于直线的拟合、估计相关系数、检验对某个系数的假设、求解置信区间、求解预测带、求解是否存在显著关系、相关图形的构造；以及对模型结果的解释与分析。
以下是本人的线性模型【蒙哥马利】第二章部分课后习题的代码及结果解释，以便对这一章进行快速理解。

2.10

26位年龄群体为25—30岁随机选取的男性，其体重与血液收缩压数据显示如下。

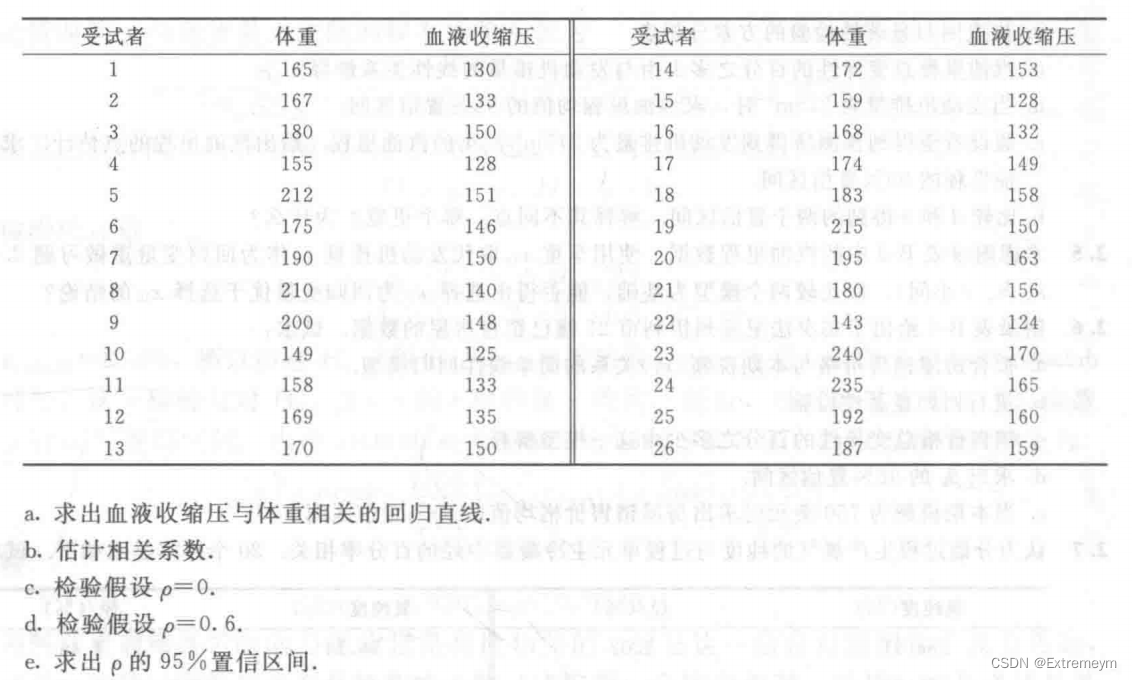
代码结果为：

library(readxl)
mydata2 <- read_excel('D:/xianxingmoxing/first/data-prob-2-10.xls')
View(mydata2)
attach(mydata2)
x=weight
y=xyssy
n=26#测试者个数
hist(x)#做体重与血液收缩压之间的直方图

z <- lm(xyssy~weight)#线性回归
z

R_pearson <- cor(x,y,method = 'pearson') #求解相关系数
R_pearson

#检验假设，假设相关系数=0
a=0
cor.test(x,y,conf.level = 0.95)
#假设H0为相关系数=0，该假设下的检验统计量为t1
t1 <- r*(n-2)^0.5/(1-r^2)^0.5#计算t1检验统计量
t1
if(t>a)
  print("拒绝H0")else
    print("无法拒绝H0")


#检验假设，假设相关系数=0.6
a=0.6
cor.test(x,y,conf.level = 0.95)
#假设H0为相关系数=0，该假设下的检验统计量为t2
t2 <- (atanh(r)-atanh(a))*(n-3)^0.5#计算t2检验统计量
t2
if(t>a)
  print("拒绝H0")else
    print("无法拒绝H0")

#置信区间
a<- cor.test(x,y)#默认即95%
z <- qnorm(0.025,lower.tail=F)#分位数
zxqj <- c(tanh(atanh(r)-z/(n-3)^0.5),tanh(atanh(r)+z/(n-3)^0.5))
zxqj

A.求出血液收缩压与体重相关的回归直线
本文视体重为自变量、血液收缩压为因变量，做回归直线结果如下：

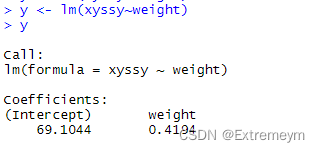
由结果显示，体重与血液收缩压的简单线性回归模型为：y=0.4194x+69.1044

B.估计相关系数

求解相关系数，并且表示出来得p=0.7735。

C.假设检验

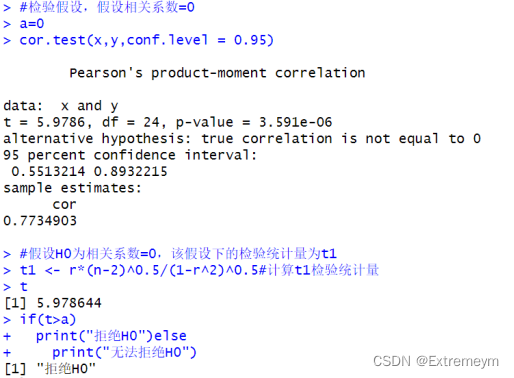
D.假设检验

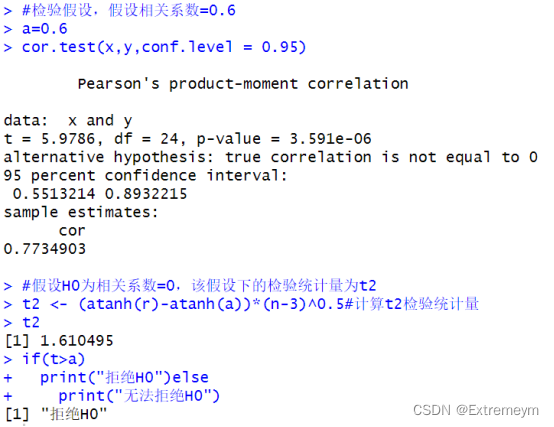
E.求出的95%置信区间

2.13

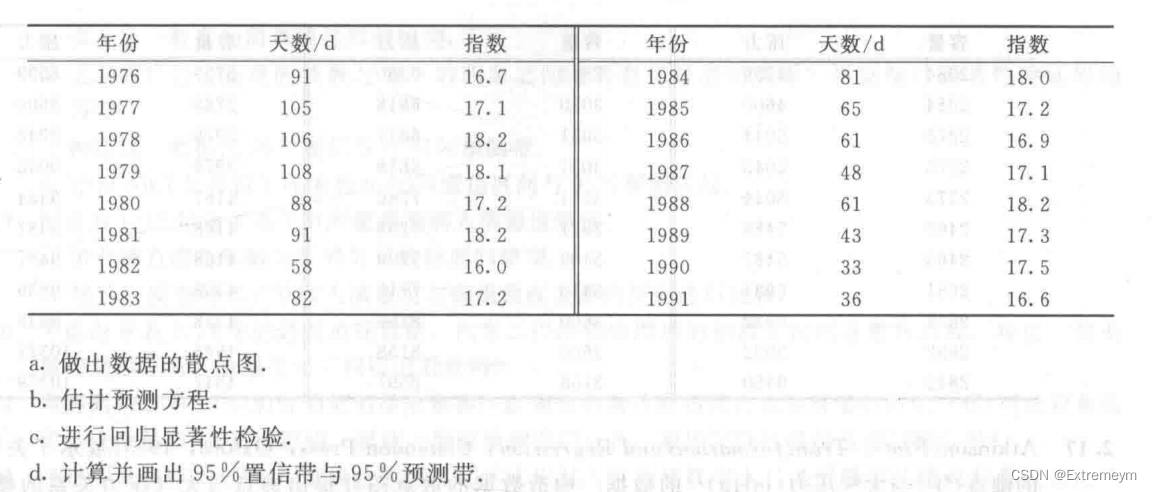
研究1976——1999年南部地区加利福利亚州空气品质的臭氧水平，超过0.2*10（-4）的天数（响应变量）取决于季节气象指数，这一指数是850mpa下的季节平均温度（回归变量）。数据如下：

library(basicTrendline)
library(readxl)
mydata2 <- read_excel('D:/xianxingmoxing/first/data-prob-2-13.xls')
View(mydata3)
attach(mydata3)
x=days
y=index

#画散点图
plot(y~x,main="季节指数变化散点图",xlab="天数",ylab="指数",pch=19)
# y~x,画标题，X坐标轴标题，Y坐标轴标题                                  

#拟合线性模型
a <-lm(y~x)
a
summary(a)
abline(a)

#置信区间
t.test(x,y)
#预测带
b<- trendline(x, y, model="line3P", ePos.x = "topleft", summary=TRUE, eDigit=5)
#"model" should be one of 
c("lin2P","line3P","log2P","exp2P","exp3P","power2P","power3P")
#ePos.表示函数结果 R2 显著性检验结果标注在图像中的哪里
#eDigit表示R2保留几位小数

A.做出数据的散点图

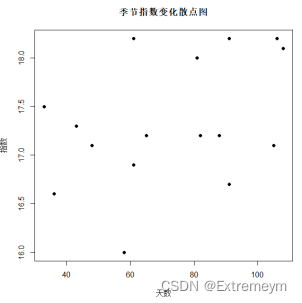
B.估计预测方程 C.进行回归显著性检验
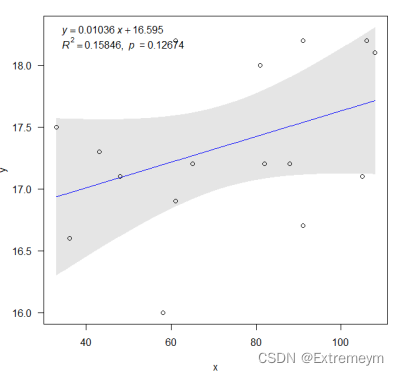
由天数与指数之间的散点关系图，大致符合一次直线，故进行直线拟合，得到下面关系式。

由拟合结果显示，指数与天数关系的简单线性回归模型为：y=0.01036x1+16.5946
且x与常数均通过显著性检验。且图像如下：

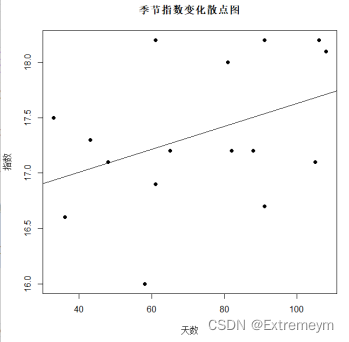
D.计算并画出95%置信带与95%预测带

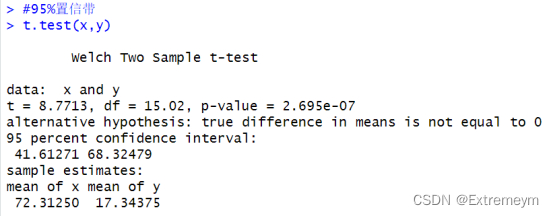
得到置信区间为：[72.31250，17.34375]，图像如下：

95%预测带为：

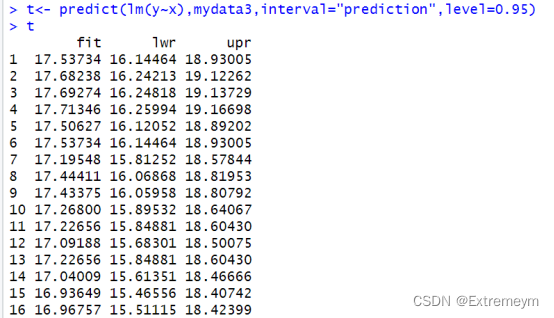
图像如下：

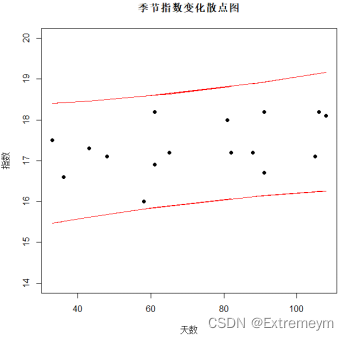
2.23

考虑简单线性回归模型y=50+10x十e，式中，e为NID(0，16)分布.假设用于拟合模型的观测值n=20对．生成这20个观测值的500个样本，对每个样本画出每个水平(r=1，1.5，2，…，10)的一个观测值。

a.对每个样本计算斜率和截距的最小二乘估计值．构造样本β0帽与β1帽值直方图．讨论这两个直方图的形状.
b.对每个样本，计算E(y |x=5)的估计值．构造所得到估计值的直方图．讨论这一直方图的形状.
c.对每个样本，计算斜率的95%置信区间．这些区间中有多少包含真实值β1=10？这是你所期望的吗？
d.对b中E(y |x=5)的每个估计值，计算95%置信区间．这些区间中有多少个包含其真实值E(ylx=5)=100？这是你所期望的吗？

#假设20个观测值x
x <- seq(0.5,10,0.5)#起始数字为1，末尾数字为10，间隔0.5
set.seed(1)#设定随机数的seed
#设定生成随机数的种子，种子是为了让结果具有重复性，使生成的随机数得以重现。

#生成四个空矩阵,放置估计值\结果值
m<- matrix(nrow=500,ncol=20)
xx<- matrix(nrow=500,ncol=1)
yy<- matrix(nrow=500,ncol=2)
q<- matrix(nrow=500,ncol=2)

#构造循环
for(i in 1:500)
  {
  a <- rnorm(n=20,mean=0,sd=4)#rnorm表示生成正态分布的随机数，sd为标准差
  a0=50
  a1=10
  y <- a0+a1*x+a
  h <- lm(y~x)
  m[i,] <- c(h$coefficients)#将每次估计值提取出来，放入数组第i行
  #置信区间
  yy[i,] <- confint(h,"x",level=0.95)#系数的置信区间
  #E(y|x)
  xx[i,] <- predict(h,new=data.frame(x=5))#将x=5时y的拟合值放入数组
  q[i,] <- predict(h,new=data.frame(x=5),interval="confidence",level=0.95)[,2:3]
  #将E(y|x)的置信区间放入数组
}


#构造系数估计直方图
a00 <- m[,1]
a11 <- m[,2]
hist(a11)
hist(a00)


#计算E(y|x=5)的估计值
eyx1 <- a00+a11*5
eyx1
#构造直方图
hist(eyx1,xlab="E(y|x=5)")


#C问
#计算a1的95%的置信区间
a1qj<- predict(h,new=data.frame(x),interval="confidence",level=0.95)
a1zxqj<-c(min(a1qj[,1]),max(a1qj[,1]))
a1zxqj
#计算区间中包含了真值10的个数
n1=0
for(i in 1:500)
{if(yy[i,1]<10&yy[i,1]>10)
{d=1}
  else{d=0}
  n1=n1+d
}
print(n1)
#length(which((a1qj[,1]==10)))#这是判断区间中是否真值10的个数



#计算E(y|x=5)的95%的置信区间，并计算包含了真值的区间个数
q[i,] <- predict(h,new=data.frame(x=5),interval="confidence",level=0.95)[,2:3]
q[i,]
#将E(y|x)的置信区间放入数组
#计算包含了真值100的个数
n2=0
for(i in 1:500)
{if(q[i,1]<100&q[i,2]>100)
{d=1}
  else{d=0}
  n2=n2+d
}
print(n2)

A.对每个样本计算斜率和截距的最小乘估计值，构造样本系数直方图，并讨论两个直方图的形状。

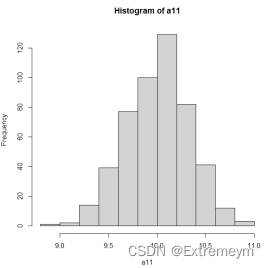
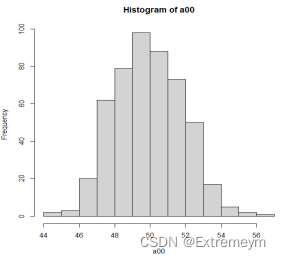
aa1为β1的最小二乘估计值，a00为β0的最小二乘估计值。由两结果图可知，两系数的最小二乘估计值均大体呈现正态分布。

B.对每个样本计算E(y|x=5)的估计值，构造估计值的直方图。

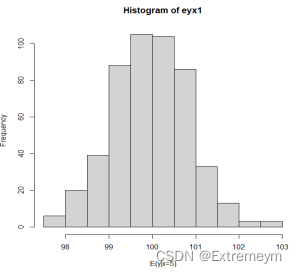
C.对每个样本计算斜率的95%置信区间，这些区间中有多少个包含真实值=10？

计算出对每个样本计算斜率的95%置信区间为[52.55249，152.05751]。

判断出来区间中有0个包含真实值β1=10。

D.对b中E(y|x=5)的每个估计值，计算95%置信区间。这些区间中有多少个包含其真实值E(y|x=5)=100？

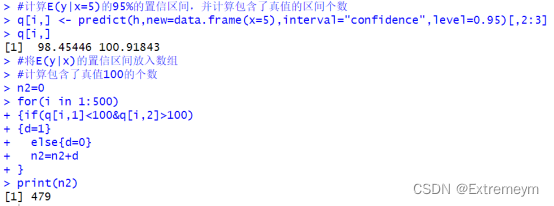
置信区间为：[98.45446 100.91843]。且每个估计值的区间中有479个包含其真实值E(y|x=5)=100？