四、希尔排序

希尔排序(Shell Sort)是 插入排序的一种。也称缩小 增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL．Shell于1959年提出而得名。

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

基本思想

先取一个小于n的整数d1作为第一个 增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行 直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量

   

=1(

   

<

   

…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。

该方法实质上是一种分组插入方法

比较相隔较远距离（称为 增量）的数，使得数移动时能跨过多个元素，则进行一次比较就可能消除多个元素交换。D.L.shell于1959年在以他名字命名的 排序算法中实现了这一思想。算法先将要排序的一组数按某个 增量d分成若干组，每组中记录的下标相差d.对每组中全部元素进行排序，然后再用一个较小的增量对它进行，在每组中再进行排序。当 增量减到1时，整个要排序的数被分成一组，排序完成。

一般的初次取序列的一半为 增量，以后每次减半，直到增量为1。

给定实例的shell排序的排序过程

假设待排序文件有10个记录，其关键字分别是：

49，38，65，97，76，13，27，49，55，04。

增量序列的取值依次为：

5，2，1

稳定性

由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的。

缩小增量

希尔排序属于插入类排序,是将整个有序序列分割成若干小的子序列分别进行 插入排序。

排序过程：先取一个正整数d1<n，把所有序号相隔d1的 数组元素放一组，组内进行 直接插入排序；然后取d2<d1，重复上述分组和排序操作；直至di=1，即所有记录放进一个组中排序为止。

三趟结果

04 13 27 38 49 49 55 65 76 97

优劣

不需要大量的辅助空间，和 归并排序 一样容易实现。希尔排序是基于 插入排序 的一种算法， 在此算法基础之上增加了一个新的特性，提高了效率。希尔排序的 时间复杂度 与增量序列的选取有关，例如 希尔增量 时间复杂度为O(n²)，而Hibbard增量的希尔排序的时间复杂度为O(

   

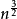)，希尔排序时间复杂度的下界是n*log2n。希尔排序没有 快速排序算法 快 O(n(logn))，因此中等大小规模表现良好，对规模非常大的 数据排序 不是最优选择。但是比O(

   

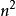)复杂度的算法快得多。并且希尔排序非常容易实现，算法代码短而简单。 此外，希尔算法在最坏的情况下和平均情况下执行效率相差不是很多，与此同时快速排序在最坏的情况下执行的效率会非常差。专家们提倡，几乎任何排序工作在开始时都可以用希尔排序，若在实际使用中证明它不够快，再改成快速排序这样更高级的 排序算法 . 本质上讲， 希尔排序算法 是直接插入排序算法的一种改进，减少了其复制的次数，速度要快很多。 原因是，当n值很大时 数据项 每一趟排序需要的个数很少，但数据项的距离很长。当n值减小时每一趟需要和动的数据增多，此时已经接近于它们排序后的最终位置。 正是这两种情况的结合才使希尔排序效率比 插入排序 高很多。Shell算法的性能与所选取的分组长度序列有很大关系。只对特定的待排序记录序列，可以准确地估算关键词的比较次数和对象移动次数。想要弄清关键词比较次数和记录移动次数与增量选择之间的关系，并给出完整的数学分析，至今仍然是数学难题。

时间性能

1． 增量序列的选择

Shell排序的执行时间依赖于 增量序列。

好的 增量序列的共同特征：

① 最后一个 增量必须为1；

② 应该尽量避免序列中的值(尤其是相邻的值)互为倍数的情况。

有人通过大量的实验，给出了较好的结果：当n较大时，比较和移动的次数约在nl.25到1.6n1.25之间。

2．Shell排序的时间性能优于 直接插入排序

希尔排序的时间性能优于 直接插入排序的原因：

①当文件初态基本有序时 直接插入排序所需的比较和移动次数均较少。

②当n值较小时，n和

   

的差别也较小，即 直接插入排序的最好 时间复杂度O(n)和最坏时间复杂度0(

   

)差别不大。

③在希尔排序开始时 增量较大，分组较多，每组的记录数目少，故各组内直接插入较快，后来增量di逐渐缩小，分组数逐渐减少，而各组的记录数目逐渐增多，但由于已经按di-1作为距离排过序，使文件较接近于有序状态，所以新的一趟排序过程也较快。

因此，希尔排序在效率上较直接插入排序有较大的改进。

希尔排序是按照不同步长对元素进行 插入排序 ，当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；当元素基本有序了，步长很小，插入排序对于有序的序列效率很高。所以，希尔排序的 时间复杂度 会比o(n^2)好一些。

#include "stdio.h"
#include "stdlib.h"
#include "string.h"

void println(int array[], int len)
{
 int i = 0;

 for(i=0; i<len; i++)
 {
  printf("%d ", array[i]);
 }

 printf("\n");
}
void swap(int array[], int i, int j)
{
 int temp = array[i];
 array[i] = array[j];
 array[j] = temp;
}

void InertionSort(int array[], int len) // O(n*n)
{
 int i = 0;
 int j = 0;
 int k = -1;
 int temp = -1;

 //{12, 5, 433, 253, 216, 7};
 for(i=1; i<len; i++)
 {
  k = i; //待插入位置
  temp = array[k];

  for(j=i-1; (j>=0) && (array[j]>temp); j--)
  {
   array[j+1] = array[j]; //元素后移
   k = j; //k需要插入的位置
  }

  array[k] = temp;//元素插入
 }
}

//nlogn
void ShellSort(int array[], int len) //
{
 int i = 0;
 int j = 0;
 int k = -1;
 int temp = -1;
 int gap = len;
 do
 {
   //业界统一实验的 平均最好情况 经过若干次后，收敛为1
  gap = gap / 3 + 1; //gap /2345 2000 都行  //O（n 1.3）
 
  for(i=gap; i<len; i+=gap)
  {
   k = i;
   temp = array[k];

   for(j=i-gap; (j>=0) && (array[j]>temp); j-=gap)
   {
    array[j+gap] = array[j];
    k = j;
   }

   array[k] = temp;
  }

 }while( gap > 1 );

}


int main()
{
 int array[] = {12, 5, 433, 253, 216, 7};
 int len = sizeof(array) / sizeof(*array);

 println(array, len);
 ShellSort(array, len);
 println(array, len);
 system("pause");
 return 0;
}