起源[编辑]
牛顿法最初由艾萨克·牛顿在《流数法》(Method of Fluxions,1671年完成,在牛顿死后的1736年公开发表)。约瑟夫·拉弗森也曾于1690年在Analysis Aequationum中提出此方法。
方法说明[编辑]
首先,选择一个接近函数 零点的
零点的 ,计算相应的
,计算相应的 和切线斜率
和切线斜率 (这里
(这里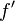 表示函数
表示函数 的导数)。然后我们计算穿过点
的导数)。然后我们计算穿过点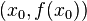 并且斜率为
并且斜率为 的直线和
的直线和 轴的交点的
轴的交点的 坐标,也就是求如下方程的解:
坐标,也就是求如下方程的解:
我们将新求得的点的 坐标命名为
坐标命名为 ,通常
,通常 会比
会比 更接近方程
更接近方程 的解。因此我们现在可以利用
的解。因此我们现在可以利用 开始下一轮迭代。迭代公式可化简为如下所示:
开始下一轮迭代。迭代公式可化简为如下所示:
已经证明,如果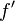 是连续的,并且待求的零点
是连续的,并且待求的零点 是孤立的,那么在零点
是孤立的,那么在零点 周围存在一个区域,只要初始值
周围存在一个区域,只要初始值 位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果
位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果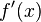 不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。
不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。
利用迭代算法解决问题,需要做好以下三个方面的工作:
一、确定迭代变量
在可以用迭代算法解决的问题中,至少存在一个可直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量。
二、建立迭代关系式
所谓迭代关系式,指如何从变量的前一个值推出其下一个值的公式(或关系)。迭代关系式的建立是解决迭代问题的关键,通常可以使用递推或倒推的方法来完成。
三、对迭代过程进行控制
在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题。不能让迭代过程无休止地执行下去。迭代过程的控制通常可分为两种情况:一种是所需的迭代次数是个确定的值,可以计算出来;另一种是所需的迭代次数无法确定。对于前一种情况,可以构建一个固定次数的循环来实现对迭代过程的控制;对于后一种情况,需要进一步分析得出可用来结束迭代过程的条件。
3示例编辑
欧几里德算法
最经典的迭代算法是
欧几里德算法,用于计算两个整数a,b的最大公约数。其计算原理依赖于下面的定理:
定理:gcd(a,b) = gcd(b,a mod b)
证明:a可以表示成a = kb + r,则r = a mod b。假设d是a,b的一个公约数,则有 a%d==0,b%d==0,而r = a - kb,因此r%d==0 ,因此d是(b,a mod b)的公约数
同理,假设d 是(b,a mod b)的公约数,则 b%d==0,r%d==0 ,但是a = kb +r ,因此d也是(a,b)的公约数。
因此(a,b)和(b,a mod b)的公约数是一样的,其最大公约数也必然相等,得证。
欧几里德算法就是根据这个原理来做的,欧几里德算法又叫辗转相除法,它是一个反复迭代执行,直到余数等于0停止的步骤,这实际上是一个循环结构。其算法用C语言描述为:
int Gcd_2(int a,int b)/*欧几里德算法求a,b的最大公约数*/
{
if (a<=0 || b<=0)/*预防错误*/
return 0;
int temp;
while (b > 0)/*b总是表示较小的那个数,若不是则交换a,b的值*/
{
temp = a % b;/*迭代关系式*/
a = b;
b = temp;
}
return a;
}
从上面的程序我们可以看到a,b是迭代变量,迭代关系是temp = a % b;根据迭代关系我们可以由旧值推出新值,然后循环执a = b; b = temp;直到迭代过程结束(余数为0)。在这里a好比那个胆小鬼,总是从b手中接过位置,而b则是那个努力向前冲的先锋。
斐波那契数列
还有一个很典型的例子是斐波那契(Fibonacci)数列。
斐波那契数列为:0、1、1、2、3、5、8、13、21、…,即 fib⑴=0; fib⑵=1;fib(n)=fib(n-1)+fib(n-2) (当n>2时)。
在n>2时,fib(n)总可以由fib(n-1)和fib(n-2)得到,由旧值递推出新值,这是一个典型的迭代关系,所以我们可以考虑迭代算法。
int Fib(int n) //斐波那契(Fibonacci)数列
{
if (n < 1)/*预防错误*/
return 0;
if (n == 1 || n == 2)/*特殊值,无需迭代*/
return 1;
int f1 = 1,f2 = 1,fn;/*迭代变量*/
int i;
for(i=3; i<=n; ++i)/*用i的值来限制迭代的次数*/
{
fn = f1 + f2; /*迭代关系式*/
f1 = f2;//f1和f2迭代前进,其中f2在f1的前面
f2 = fn;
}
return fn;
}
4C语言代码编辑
double func(double x) //函数
{
return x*x*x*x-3*x*x*x+1.5*x*x-4.0;
}
double func1(double x) //导函数
{
return 4*x*x*x-9*x*x+3*x;
}
int Newton(double *x,double precision,int maxcyc) //迭代次数
{
double x1,x0;
int k;
x0=*x;
for(k=0;k<maxcyc;k++)
{
if(func1(x0)==0.0)//若通过初值,函数返回值为0
{
printf("迭代过程中导数为0!\n");
return 0;
}
x1=x0-func(x0)/func1(x0);//进行牛顿迭代计算
if(fabs(x1-x0)<precision || fabs(func(x1))<precision) //达到结束条件
{
*x=x1; //返回结果
return 1;
}
else //未达到结束条件
x0=x1; //准备下一次迭代
}
printf("迭代次数超过预期!\n"); //迭代次数达到,仍没有达到精度
return 0;
}
int main()
{
double x,precision;
int maxcyc;
printf("输入初始迭代值x0:");
scanf("%lf",&x);
printf("输入最大迭代次数:");
scanf("%d",&maxcyc);
printf("迭代要求的精度:");
scanf("%lf",&precision);
if(Newton(&x,precision,maxcyc)==1) //若函数返回值为1
printf("该值附近的根为:%lf\n",x);
else //若函数返回值为0
printf("迭代失败!\n");
getch();
return 0;
}
5C++代码编辑
//此函数是用来求一元3次方程ax^3+bx^2+cx+d=0的解
//比如 x^3-27=0,我们就可以输入1 0 0 -27,这样我们就可以得到一个解
#include<iostream>
#include<cmath>
using namespace std;
int main()
{
double diedai(double a,double b,double c,double d,double x);
double a,b,c,d;
double x=10000.0;
cout<<"请依次输入方程四个系数:";
cin>>a>>b>>c>>d;
x=diedai(a,b,c,d,x);
cout<<x<<endl;
return 0;
}
double diedai(double a,double b,double c,double d,double x)
{
while(abs(a*x*x*x+b*x*x+c*x+d)>0.000001)
{
x=x-(a*x*x*x+b*x*x+c*x+d)/(3*a*x*x+2*b*x+c);
}
return x;
}
6matlab代码编辑
定义函数
function y=f(x)
y=f(x);%函数f(x)的表达式
end
function z=h(x)
z=h(x);%函数h(x)的表达式
end
主程序
x=X;%迭代初值
i=0;%迭代次数计算
while i<= 100%迭代次数
x0=X-f(X)/h(X);%牛顿迭代格式
if abs(x0-X)>0.01;%收敛判断
X=x0;
else break
end
i=i+1;
end
fprintf('\n%s%.4f\t%s%d','X=',X,'i=',i) %输出结果










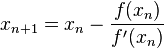
















 2938
2938

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








