有限元非线性求解算法——Newton-Raphson

冬生亦东生

已于 2024-12-22 11:45:16 修改

阅读量6.8k

点赞数 9

分类专栏：数值计算文章标签：算法机器学习人工智能

于 2023-06-10 19:33:30 首次发布

本文链接：https://blog.csdn.net/qq_46417931/article/details/131145656

版权

数值计算专栏收录该内容

6 篇文章

订阅专栏

文章介绍了有限元方法在解决非线性静力问题时如何转化为矩阵方程，并重点讨论了牛顿-拉夫森迭代法在求解此类问题中的应用。通过案例展示了迭代过程，以及如何处理收敛性和初始值的选择。文章还提到了实际工程中的荷载增量步和容差控制策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

0. 前言

有限元静力问题的求解实际上最终通过某些理论方法（最小势能原理，虚功原理，加权残值法等）转化为 K(u)u=F 形式的矩阵方程（非线性方程或者方程组）的求解，这里K是全局刚度矩阵，通过力学三大方程和试函数求得；u是节点位移向量，是待求的未知数，其中可以通过位移边界条件减少未知数数量；F是节点荷载向量，是由荷载边界条件依据静力等效转化为节点荷载向量。因此求解非线性方程组，研究求解算法是一个难点，求解算法主要为增量法和迭代法，实际上真正有限元求解时是两种方法结合使用的。

1.算法来源

Newton-Raphson(牛顿-拉夫森)迭代法是一种求解方程根的常用方法。它使用函数的一阶和二阶导数信息来高效地逐步逼近方程根。

略去高阶项，整理可得到下式

需要注意的是，牛顿-拉夫森迭代法并不总是收敛。如果函数f(x)在某些点上的一阶或二阶导数为0，或者在根周围有一定的震荡行为，都可能导致算法无法收敛。此外，如果初始点x0选取得离根过远，也可能会导致算法无法收敛。因此，在实际使用中，需要根据实际情况灵活选择初始点、步长和迭代精度等参数，以保证算法的准确性和可靠性。下面图中展示了算法的格式。

非线性方程

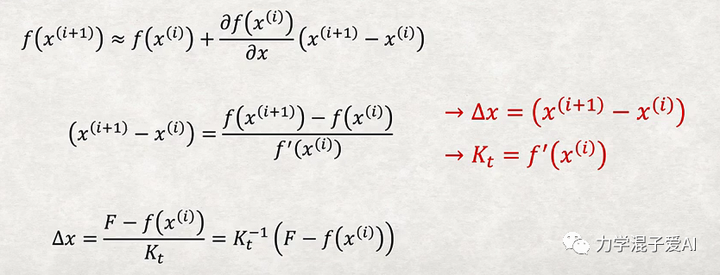
非线性方程组

2. 非线性求解迭代过程

下面解释下有限元的求解非线性问题的迭代过程。上图是某个荷载增量步的求解示意图。

第一次迭代前，需要给一个位移初始值（假定的位移值），实际上位移初始值可以随便给，但是考虑到算法的实用性，收敛性和收敛速度，我们一般肯定希望初始值要么取值具有一般性或者接近真实位移值。一般初始位移值是通过当前荷载增量和初始刚度的比值来确定，在这里初始刚度就是当前增量开始时的刚度矩阵，荷载增量是人为设置的（有限元软件里面也可以设置，例如abaqus中设置如下图）

荷载步内求解迭代过程

然后根据当前给定的位移值求出当前的刚度矩阵（记住刚度矩阵与材料属性和几何参数有关），并计算当前位移匹配的结构内力，接着计算内力与当然外载F的差值（也可以用位移容差控制，实际有限元中考虑荷载容差和位移容差），如果这个差值小于设置的容差，那么就停止迭代，否则继续重复上述步骤。

3.案例

(*Material Nonlinearity Example*)
Clear["Global`*"]
(*Parameters*)
L = 1.0;
A = 1;
p = X1^2;
(*Newton-Raphson Parameters*)
Xi = 1;
ErrorLimit = 0.5;
maxIter = 20;

(*Stress-Strain Relationship*)
s = 10*u'[X1] + 100000*u'[X1]^3;

(*Exact solution*)
DE = D[s*A, X1] + p;
sol = NDSolve[{DE == 0, u[0] == 0, u[L] == 0}, u[X1], X1];
uExact = u[X1] /. sol[[1]];
Plot[uExact, {X1, 0, L}];

(*RR Approximation，最小势能原理*)
(*此案例相当于三节点二次单元*)
(*Approximation Function*)
uApprox = a0 + a1*X1 + a2*X1^2;
(*Essential Boundary Conditions*)
BC1 = uApprox /. {X1 -> 0};
BC2 = uApprox /. {X1 -> L};
sol1 = Solve[{BC1 == 0, BC2 == 0}, {a0, a1}]; {a0, a1} = {a0, a1} /. 
  sol1[[1]];
uApprox;

(*Total Internal Strain Energy*)
S = 10*e + 100000*e^3;
SED = Integrate[S, {e, 0, e}];          (*单位体积应变能*)
e = D[uApprox, X1];
TSE = Integrate[SED, {X1, 0, L}];              (*总应变能*)

(*work*)
w = Integrate[p*uApprox, {X1, 0, L}];           (*外力功*)
(*Potential Energy*)
PE = TSE - 
   w    ;                                  (*偏导等于0，对应的方程组的解，即为代求*)

(*Newton-Raphson Method*)
ai = {a2};
Func = D[PE, a2] ;              (*我们要这个方程组的解,这里是解a2*)

Kt = D[Func, a2];

 {
 {For[i = 1, i <= maxIter, i++,
   
   (*calculate Function and Kt at currentIteration*)
   FuncIter = Func /. {a2 -> Xi};
   KtIter = Kt /. {a2 -> Xi};
   
   (*Solving for Delta x*)
   Delta = (-1)*FuncIter/KtIter;
   
   (*Finding xi for Next Iteration*)
   XInit = Xi;
   Xi = Xi + Delta;
   
   (*Break Loop Once Convergence 0ccurs*)
   Error = (Delta/XInit)*100;
   If[Abs[Error] <= ErrorLimit,
    Print["Analysis Converged ! "];
    Print[" Coefficient a2 = ", Xi]; Print["Error = ", Error, "(%)"];
    a2 = Xi;
    Conv = 1;
    Break[]];
   (*Track Results*)
   Print["Iteration: ", i];
   Print["coefficient a2 = ", Xi]; Print["Error = ", Error, "(%)"];
   (*Error Message if Max Number of IterationsReached*)If[i == maxIter,
    Print["Max of Number of Iterations Reached"]];
   ]},
 {\[Placeholder]}
} 
uApprox
Plot[{uExact, uApprox}, {X1, 0, L}, PlotLegends -> {"Exact" , "FEA"}, 
 AxesLabel -> {"Bar Length", "Displacement"}, AspectRatio -> 0.5]

下图显示了有限元解与精确解的沿着杆长的位移分布图，有一定的误差主要是这里为了简单起见，仅仅用了一个单元（三节点二次单元），想测试单元数量对结果精度的影响，可以将我的第一篇有限元笔记的代码和当前的结合起来修改下即可，这篇笔记旨在学习了解非线性有限元计算的的思路方法。

4. 结语

我一直都在分享笔记，是因为当前我也处于学习理论的状态，不过笔记较多，我分享的主要是之前一段时间的学习笔记，加上我当前的部分理解，重新整理呈现了出来。目前我在寻找损伤力学，断裂力学，张量分析，离散元等方面的优秀教材资料等，希望大家能分享给我，一起学习交流。获取更多资料和学习交流欢迎大家关注公众号冬生亦东生，分享旨在本人复习和交流