[BZOJ2301]HAOI2011 ProblemB|莫比乌斯

学了一下莫比乌斯反演，被虐的好惨啊。。

    首先下界太碍事了，用容斥原理把一个询问拆成四个，把下界扔掉。。（x，y）=k，也就是（x/k，y/k）=1，所以可以把上界都除以k，设除完之后为n，m，那答案就是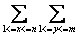（x，y）==1。。

    在学的时候我看到了两种转化方法，PoPoQQQ的和iwtwiioi的，我觉得PoPoQQQ的好理解一点，不过后来也理解了iwtwiioi的。。

    我觉得他们都写的很不错，Orz。。我直接扔链接好了。。

PoPoQQQ

iwtwiioi

我的笔记

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<memory.h>
#define N 50005
using namespace std;
int n,a,b,c,d,k,i,j,cnt,t,mu[N],s[N],p[N];
bool u[N];
void getmu(int n)
{
	int i,j;
	memset(u,0,sizeof(u));
	mu[1]=1;cnt=0;s[1]=1;s[0]=0;
	for (i=2;i<=n;i++)
	{
		if (!u[i])
		{
			p[++cnt]=i;
			mu[i]=-1;
		}
		s[i]=s[i-1]+mu[i];
		for (j=1;j<=cnt&&i*p[j]<=n;j++)
		{
			u[i*p[j]]=1;
			if (i%p[j]==0) 
			{
				mu[i*p[j]]=0;
				break;
			}
			else mu[i*p[j]]=-mu[i];
		}
	}
}
int ans(int a,int b)
{	
	int i,pos,sum=0;
	for (i=1;i<=min(a,b);i=pos+1)
	{
		pos=min(a/(a/i),b/(b/i));
		sum+=(s[pos]-s[i-1])*(a/i)*(b/i);
	}
	return sum;
}
int main()
{
	scanf("%d",&n);
	getmu(50000);
	for (t=1;t<=n;t++)
	{
		scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
		a--;c--;
		a/=k;b/=k;c/=k;d/=k;
		printf("%d\n",ans(b,d)-ans(a,d)-ans(b,c)+ans(a,c));
	}
}